前頁 |▼| 次頁
第25章 科学的方法
学問と科学の定義が、「一定の目的と方法の下に行われる、様々な事象の研究活動であり、その研究活動によって得られる知」です。その目的は、「真理の追究」であり、「今現在における、より正しいとされる物事・事柄・道筋を明らかにすること」です。この目的が、学問と科学の1つの柱となります。
それでは、学問と科学のもう1つの柱である「一定の方法」とな何でしょうか。学問と科学において、どのような方法の下で研究活動が行われているかを学びます。その際に、正しさを考える上で、重要となる実証と反証という考え方も紹介します。
| 目次 |
| 1 意義 2 科学的方法 3 理論とモデル 4 観察可能な含意と概念的定義と操作的定義 5 変数 6 まとめ テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 意義
学問と科学とは、「『真理の追究』を目的として『一定の方法』の下に行われる研究活動」のことですが、「一定の方法」とは何でしょうか。今から、これについて考えます。
この「一定の方法」が、いわゆる学問的方法、あるいは、科学的方法と呼ばれるものです。
「一定の方法」の約束事の下に、研究され、証明された事柄だから、皆が正しいと認めることになります。「一定の方法」とは、正しいことを証明するためのルールや手続きだと言えます。
したがって、科学的方法のルールに則って証明できていれば、正しいと認められます。
逆に、科学的方法に則っていないならば、結論だけ正しく見えても、その論理的な整合性や結論の正しさは何も保証されておらず、それ故に、正しいとは認められません。
このように、学問的であったり、科学的であったりするためには、「一定の方法」の下で行われることが必要になります。そして、それ故に、皆が正しいと認めるのだということになります。
そこで、まずは科学的方法の基本的な手順について学びます。
なお、これ以降この講義では、科学的方法を、科学的手法と言い換えたり、学問的方法や学問的手法と言い換えることもありますが、すべて同じ意味で捉えておいて構いません。英語では、scientific method となります。
それでは、科学的方法を紹介します。と言っても、実は、科学的方法の主要かつ基礎的な事項は、第 I 部 論理的思考で説明してしまいました。
ですから、ここで改めて一から手取り足取り説明し直すことはしません。演繹法と広義の帰納法についての基礎は知っているという前提で、学問や科学の方法論について説明します。
この科学の方法は、第 I 部 論理的思考 第6章 仮説推論で説明した仮説推論の内容と大きく被ります。
大きく分けて、帰納法、演繹法、解釈の3つの方法が中心となります。
2 科学的方法
それでは学問と科学の「一定の方法」・約束事がどのようなものかを見て行きましょう。
科学は、何かを見て気付くことから始まります。
何かを見ることは、観察といったり観測と言います。英語では、obeservationです。
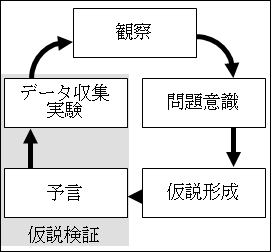
図25.1.科学的方法 
観察をすることで、何かに気付き、問題意識を持ちます。英語では、questionです。
図25.1.科学的方法 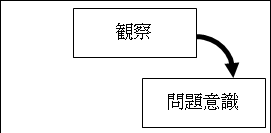
そこで、どうしてこうなるのだろうか、何故こうなるのだろうか、または、いつもそうなるのだろうか、といったことを考えて、その問題意識に対して、理由や原因などの説明をします。
この観察事実に対する合理的な説明が仮説です。英語では、hypothesisです。
したがって、仮説は、観察したことを基にして論理的に考えると、このように説明することができる、という意味で、「仮」の「説明」になります。
図25.1.科学的方法 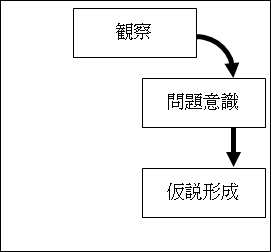
この仮説を形成することを、仮説形成と言います。仮説を形成することを英語で言えば、formulate hypotheses ですね。hypothesis の複数形は、hypothesises ではなく、hypotheses であることに注意してください。
仮説を形成すると、観察して抱いた問題意識に対しての説明ができた気になってしまいがちで、めでたしめでたしと思ってしまいます。が、しかし、それでは科学的ではありません。確かに、仮説は、観察された事実を基にして論理的に考えたら、そう説明できるという合理的な説明ではありますが、その仮説が正しいか誤っているかは、実の所、分かっていません。
したがって、形成した仮説が実際の事実に沿ったものになっているのかを確かめないといけません。
この仮説が本当に正しいかどうかを確かめること仮説検証と言います。仮説を検証することを英語で言えば、test hypotheses です。
図25.1.科学的方法 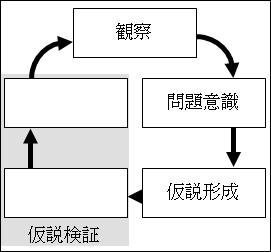
それでは、仮説検証をするためには、どうすればいいでしょうか。つまり、仮説が正しいことをどうやって証明したらいいでしょうか。
仮説が正しいとしたら、何が予測できるか、ということを考えます。
この仮説から何が予測されるか、ということを予言と言います。予言ではなく、そのまま予測と言ってもいいのですが、英語では predictions と言うので、ここでは予言という言葉を使います。
図25.1.科学的方法 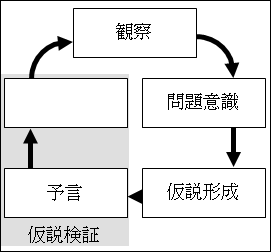
したがって、仮説検証は、予言を確認することで行われます。
まず、仮説が正しいとしたら、結果としてどうなるか、という予言をします。その予言が実際に確認できれば、仮説が正しいと言えます。
第 I 部の復習になりますが、なぜ予言が観察されれば仮説が正しいと言えるのかは、仮説形成のされ方を見れば明らかです。
仮説は、観察して得られた事柄や事実を根拠たる前提として、論理的に推論して、結果を予言しています。
観察して得られた事柄や事実を根拠たる前提としていることは、実際に観察されているのだから、正しいこと、つまり真であることを意味します。
さらに、論理的に推論していることは、正しい推論の形式に則っていることを意味しています。
そもそも、仮説を形成するときに論理的に破綻した説明をしていたら、仮説となり得ません。ですから、正しい推論の形式に則っており正しいことは、当たり前のことではあります。
これで、根拠たる前提と推論の形式が正しいことが分かります。しかし、後1つ正しいかどうかが分からない要素があります。それが仮説から予測される結果たる予言です。
この予言が正しい、つまり真であることだけが、未確認になっています。
図25.2.予言と仮説検証の関係
|
ですから、この結果たる予言が観察されたり、証明されれば、仮説が正しことが分かります。
今説明した、仮説の正しさについての検証が、その予言が確認されるか否かに関わっていることを、論理的な主張の形式に即して考えると、このようになります。
仮説による説明が、根拠たる前提となります。仮説自体は論理的に形成されているので、推論の形式に則っています。
仮説による予言が、結論になります。論理的に形成された仮説から、論理的に結果が予言されます。
したがって、根拠たる前提と結論は、もちろん論理的な推論によって繋がっています。この繋がりを単純化・簡略化して言えば、「ならば」という言葉に集約できます。
図25.2.予言と仮説検証の関係
|
これを踏まえて極限にまで単純化して、「仮説ならば予言」と言えます。
「前件P ⇒ 後件Q」に即して言えば、根拠たる前提=仮説=前件P、結論=予言=後件Q となります(第2章 推論方法の基礎 5 条件法参照)。
そうすると、仮説形成段階では、根拠たる前提=仮説=前件Pが真であり、推論の形式も正しいことが分かっています。
しかし、結論=予言=後件Qが真であるのか否かが分かりません。
そこで、仮説検証を行うことで、結論=予言=後件Qが実際に存在すること、つまり真であることを証明します。
予言された結果が実際に確かめられたら、予言は正しい、つまり真と言えます。
逆に、予言された結果が実際に確かめることができなければ、予言は正しくない、つまり偽となります。
ここで、真理値表を思い出してください。
| P | Q | P ⇒ Q | |
| 真 | 真 | 真 | |
| 真 | 偽 | 偽 | |
| 偽 | 真 | 真 | |
| 偽 | 偽 | 真 |
今回は、根拠たる前提=仮説=前件Pが真であり、推論の形式も正しいわけすから、結論=予言=後件Qの真偽次第で、「P ならば Q」全体の真偽が決まります。つまり、
結論=予言=後件Qが真であれば、「P ならば Q」が真になります。したがって、仮説は全体として正しくなります。
結論=予言=後件Qが偽であれば、「P ならば Q」が偽になります。したがって、仮説は全体として正しくないことになります。
このように、仮説検証で仮説が正しいかどうかは、予言が実際に確認できるかどうかに懸ってくることが分かります。
図25.2.予言と仮説検証の関係
仮説の真偽は予言の真偽に関わる ↓ 仮説検証は予言を調べる |
そうすると、仮説検証のためには、予言が真である、つまり正しいと言える情報を集めたり、実験をしたりすることになります。情報はデータとも言います。
データ収集あるいは実験になります。英語では、gather data or experiment と言ったところです。
図25.1.科学的方法
仮説が成立している状況の情報を集めます。
あるいは、仮説が成立している状況を自ら作りだして、実験をします。
これで、予言と合致したデータや実験結果が得られれば、予言が正しいと分かり、仮説が正しいことが証明できます。
もし予言と合致したデータや実験結果が得られなければ、予言と矛盾するので、予言が正しくないと分かり、仮説が正しくないことが明らかになります。
こうして、観察から始まる一連の仮説形成と仮説検証が終わります。
しかし、一回終わったら終わりではありません。仮説検証が終われば、仮説が正しくても正しくなくても、観察したのだから、新たな問題意識に繋がって行きます。
例えば、仮説が正しかった場合、より良い仮説はないのか、または仮説を精錬できないか、といったことが考えられます。
または、その仮説が異なる環境や状況・場合に適用したらどうなるのか、果たして同じ結果が得られるのだろうか、それとも違う結果になるのだろうか、といった仮説を拡張してみることも考えられます。
逆に、仮説が正しくなかった場合でも、仮説のどこに問題があったのだろうかと考え、仮説を修正して再度の検証をしたりします。
または、どう頑張って修正しても仮説が正しくなりそうになければ、仮説を破棄したりすることもあります。
このことから分かるように、仮説形成も仮説検証はたった1回で終わることの方が珍しいです。観察から始まり仮説の形成と検証を循環しながら、精錬・拡張、修正・破棄をして発散と収束を繰り返しながら、正しい仮説ができあがって行きます。
そして、自分で仮説形成と検証を何度か繰り返すと、仮説が無駄なく整理されていき、正しいことについて自信が持てます。それでも、どんなに仮説が正しく思えても、自分独りだけでは、何か見落としていたり、論理的な欠陥に気付いていないことも十分あり得ます。というか、そういうことの方が多いです。
ですから、自分の仮説を論文に書いて公に発表します。
そうすると、色々な科学者がその論文を読んで、もし仮説に論理的な欠陥やデータの不備などがあれば、それらを指摘してくれます。
また、実験結果が単なる偶然ではなく本当に得られるかどうかを再度検証してくれます。
こうした再度の検証を追試と言います。英語では、retestです。
こうして、第三者による追試を経て、何度か仮説が修正されたり拡張されたりしていきます。そして、もしその仮説が多くの人に正しいものと認められるようになったら、学問と科学の正しい知識として扱われたり、誰もが認める客観的な「事実」として扱われるようになります。つまり、仮説は誰もが認める定説 となります。
以上のように科学的方法を用いることで、第 I 部 論理的思考や第 II 部 論理的な問題解決で正しいものとして扱ってきた知識、事実が作られます。仮説形成と仮説検証の時点で、何度も試行錯誤しており、さらに追試によって第三者の見解も加わるので、かなり客観的であり、より正確に事実を説明していると考えられることに納得が行くかと思います。
3 理論とモデル
仮説が、かなりの手間暇をかけて証明されていることが分かったかと思います。こうして手間暇をかけて証明された仮説は、ほんの一部、1つの事例のことしか説明しないものもあれば、色々な事柄を1つで説明できたりするものもあります。
特に後者のような仮説を、理論と呼びます。英語では、theoryです。
理論とは、個々の現象に対する法則的、統一的な説明と言えます。したがって、理論は、個別的で具体的な仮説をより一般化したものだと考えることができます。
図25.3.仮説と理論 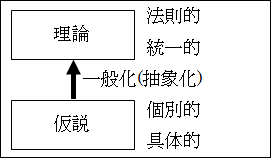
このように、理論は、個別的で具体的な仮説を一般的で抽象的にしたものと言えます。
ですから、理論は、現実に起きる様々なことを説明できることになります。現実を理解するのに役立つので、理論は、非常に便利なものです。
また、理論の成り立ち方が、個別的で具体的な仮説を一般的で抽象的にしたものだから、理論は、複数の仮説が組み合わされて体系化されたものであることも多いです。もちろん、これは、理論が1つの仮説で成り立つ場合もあることを否定しているわけではありません。
そして、理論も仮説から出発して形成されているので、基本的には、検証によって正しいことが証明される必要があります。
しかし、理論は、1つの仮説に比べたら複雑です。また、一般化しているので、個別的で具体的な要素を切り捨てている(捨象)ことも多いです。
したがって、たとえ理論が正しいことが現段階では証明されていたとしても、それが完全で完璧なものであると考えるの危険です。
理論が適用できる場合が限られていること、理解するのに便利なように具体的な要素を捨てて抽象化していることを、しっかりと自覚することが大切です。
理論と現実が食い違った場合に、現実を無視して理論が正しいと考えたりしないように気を付けてください。
ここで、理論が現実を説明し、理解するために役に立つのだということが分かったところで、モデルという考え方を紹介します。
モデルと言うと、男子はプラモデルを、女子はファッションモデルを思い浮かべる人が多いかもしれません。
プラモデルは、実際にある戦艦や飛行機、架空のロボット等をプラスチックで再現したものです。日本語で言えば、模型と言われるやつです。プラモデルは、実際の戦艦でも飛行機でもありませんがそれらを縮尺を変えて、図面に落とし込み、そこからまるで本物そっくりに再現しています。プラモデルで再現されたものは、本物ではありません。しかし、本物よりは小さいですがそっくりに再現されています。
ファッションモデルも、服をどうやって着たらいいのかというお手本です。モデルになっている人は、あくまで服を美しく見せるため媒体であって主役ではありません。ファッションモデルを使って服をどう着ると良いのかを示すことで、服だけを見せるよりも、人に服をどう着たら良いのかを理解しやすく説明できます。ただし、実際に服を着るあなたとファッションモデルは違う人です。このように、ファッションモデルは実際に着るあなたとは違うけど、ひとつの手本として機能しているのが分かります。
これで、モデルの意味が漠然とですが掴めたかと思います。つまり、モデルは、現実の本物それ自体ではなく、それを再現したり、それを理解しやすいように模範を示すものです。英語では、model と言います。科学でもモデル思考は大切になります。
そして、科学におけるモデルとは、現実の世界を理解したり、定義したり、測定したり、あるいは可視化するために、現実の世界の特徴的な部分を抜き出し再現したものです。
図25.4.モデル 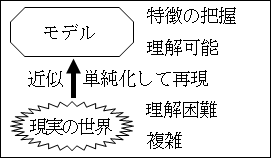
それでは、なぜ現実の世界をモデル化する必要があるのでしょうか。
その理由は、ちょっと考えたら分かると思いますが、そもそも現実をそっくりそのまま全く同じように再現することは不可能に近いからです。
現実は複雑怪奇で、そのまま理解することは困難です。ですから、私達は自分が理解できる形に落とし込んで理解しようとします。
つまり、複雑で理解困難な現実の世界を、理解できる形にその特徴を単純化して再現したものがモデルと言えます。
したがって、モデルは現実の世界の近似でもあると言えます。近似とは、英語では approximation と言い、似ていることを意味します。
現実の世界をそのまま再現することはできないので、モデルによって、現実の世界と近似した世界を考えることができるようになります。
例えば、肖像画を描くとき場合を思い浮かべてください。
肖像画は人物を描くわけですが、髪の毛一本一本同じ様に描いて再現するのは無理で、だいたい髪型の輪郭に合せて、色を再現するくらいで落ち着くはずです。このように、特徴的な部分を再現すれば、現実を擬似的に再現できていると人間は認識できます。その肖像画は、人物そのものではないのは分かりますが、本物と近似しており、本物と考えても差し支えのないものになっています。
科学でも、本質的で重要な要素に絞って単純化することで、近似して現実を再現 します。これがモデルの作り方です。
そして、モデルの便利なところは、現実の予測に役立つことです。
すべてが同じではないが現実の特徴を再現したモデルの中で起きたことは、現実の世界でも起きることが予測できます。
複雑な現実の世界では分かり難かった現象も、単純化されたモデルの中で観察すれば、その現象がどのように起きるのかが分かりやすくなります。
さらに、条件を変えてみれば、現象がどうのように変化するか、といったことも簡単に観察できるようになります。
このように、モデルは、複雑に入り組んだ現実それ自体をそのまま認識できない人間の能力を補ってくれます。現実を単純化して再現したモデルなら、考えるべき要素・観察すべき要素が減っており、本質的で重要なものだけを考えればよくなっているからです。これによって、人間は「現実」を格段に理解しやすくなります。
ところで、この科学的な思考の代表とも言えるモデル思考に対して、苦手意識を持つ学生が最近多い気がします。
いや、苦手の人の同世代に占める割合は減っていないのかもしれません。また、二昔前なら科学的思考に不慣れな人は大学に進学しなかったので、目立たなかっただけかもしれません。それが、一昔前あたりから東京を中心に私立大学の文系学部の人気が上がり、科学的思考を養うのに適切な理数系の教科をほとんど勉強せずに大学生になっても恥かしくない風潮が出てきました。そして今、少子化とAOと推薦入学が多く、国立大学ですら競争圧力が減っています。入試問題を解くことで、科学的思考がどういうもかを経験せずに、定期試験は単純な暗記で切り抜けて終わらせてしまう人が多くなるのも無理はないのかもしれませんが。入試問題も知識偏重と批判されていますが、そんなことよりももっと酷い状況に陥っている気がしてならない昨今ですね。まぁ、愚痴っても仕方ないので、ここでらで終わりにします。
苦手な人が多い気がする原因が何なのかはともかく、物理の問題を例にとってモデル思考の利便性についてもう少し説明します。皆さんも、物理の問題で、「ただし、摩擦は考えないものとする」とか「空気抵抗は考えない」とかといった文言を見かけたことがあるかと思います。こうして条件を設定して現実を単純化すると、変数が減り、力の大きさや質量等のみを変数として考えればよくなります。
科学的な考え方が苦手な人は、この仮定に混乱したり、「そんな世界なんてありえないし、問題を解く意味が無いじゃん」と思って理科を拒絶したりしてしまう傾向があります。
しかし、こうした本質的で重要な条件のみを考えるということが、モデルで考えるという方法の1つの表れなのです。
複雑なことを複雑なまま考えることは、非常に難しいです。馬鹿だから理解できないのではありません。やろうとしていることが難しいから、理解が難しいのです。
そこで、天才でもない人でも理解できるようにしたものが、モデルになります。
先ずは、モデルによって、必要最低限の条件だけでいいから、物事を簡略化・単純化して、そこから物事を考えて、本質を理解しながら現実を理解していくことになります。
もちろん、実際に自動車を走らしたり、飛行機を飛ばすときには、摩擦や空気抵抗は考えないといけません。現実の世界をできるだけ忠実に理解しようとすると、必然的に変数の個数は多くなります。しかし、それは最初の一歩を理解した後のことです。基本的なモデルの理解なしに、より複雑で応用的なモデルを扱うことは難しいです。
もし自分が馬鹿だからと自覚しているのなら、現実を説明し理解するために、単純化されたモデルで考えるということに慣れる努力をしてみてください。モデルの特徴を理解して、実際にモデルを使って、色々と考えていけば、現実の世界そのものではなくても、その片鱗を理解できるようになります。
モデルが現実の世界を理解したり説明するために用いられる道具、方法だということが理解できたかと思います。ここで、論理(ロジック)ツリーや論理ピラミッドなどで説明した枠組み framework で考えるという方法に似ているなと感じた人がいるかと思います。
モデルも枠組みも、複雑で把握し難い対象を理解するために単純化したり、考えるべき要素を予め示してくれるものです。
どちらとも、対象をどのように考えればいいのかという視点を提供してくれています。正直に言って、両者に大きな違いはありません。それでも敢えて違いを言うならば、
枠組みは、現実の対象の全体像やそれを構成する要素の関係性を表して、対象の把握の仕方を教えてくれる道具です。
モデルは、現実の対象の特徴的で考えなければならない要素のみを単純化して再現したもので、対象の動き方やそれの捉え方を教えてくれる道具です。
さらに問題分析に落とし込んで言えば、枠組みは論理ツリーで活躍するのに対して、モデルは因果関係図で活躍する、という傾向があります。
論理ツリーは、対象を個別的で具体的な要素に分解するための道具でした。これは、分析の対象の構造を整理するのに有効です。したがって、全体像や構成要素の関係性の把握に役立つ枠組みとの相性が良かったです。
因果関係図は、複数の事象の関係性と繋がりを分析するための道具でした。これは、対象の因果関係を整理するのに有効です。したがって、現実の対象の特徴的で必須の要素のみに単純化して再現するモデルとの相性が良いです。
ただし、枠組みとモデルのこのような相違点を説明しましたが、特にその区別に拘る必要はありません。
どちらとも、対象の捉え方や視点を提供しているのであり、似たようなものです。枠組みは商業活動で多く使われ、モデルは自然科学で多く使われることが多いといった具合ですが、実際に区別なく使われている事例もあります。細かいことは気にしなくても大丈夫です。今は特に気にせず、将来自分の進む専門分野で明確に区別されていたら、その使い方に従っていればいいです。
さて、理論とモデルについて説明しました。
理論とモデルは、どちらとも現実の対象を説明している点で共通しており、同じ意味で使われることも多くあります。区別がややこしく感じて、理解できないと思ったら、専門分野によって理論やモデルの用語の使い方もまちまちなので、大きく捉えて、理論=モデルと考えていても問題ないです。これも、色々と深く勉強して行けば、自ずと微妙な違いが分かって来ます。
4 観察可能な含意と概念的定義と操作的定義
仮説が観察事実に対する合理的な説明であり、理論が個々の現象に対する法則的・統一的な説明するもので、モデルが現実を単純化して近似して再現したものだということが分かりました。
そして、仮説であろうと、理論であろうと、モデルであろうと、それが正しいことを証明するには、予言が正しいかどうかを調べることが大切です。つまり、予言で述べられる事実が実際に存在することを確認することが必要でした。ですから、仮説検証でのデータ収集や実験では、予言に適合する事実を観察することになります。
しかし、いつでも事実を直接観察できるとは限りません。仮説がかなり抽象的であったり、目に見えないものであったりする場合には、直接観察ができないことが多いです。
直接観察できない場合は、どうしたらいいのでしょうか。観察できない場合は、仮説は仮説のままにして諦めるしかないのでしょうか。このことについて考えます。
まず直接観察できるものの例として、「ボールの速さは、加える力の大きさに依存する」という仮説を考えてみましょう。
| (25.1)次の仮説が正しいと証明するために、結果として観察されるべき事実の予言は何か [仮説] ボールの速さは、加える力の大きさに依存する |
これは、わざわざ結果の予言なんか考えずとも、腕の振りや投げ方から加える力の大きさが何となく分かり、ボールの速さも見で分かります。つまり、直接観察できる仮説です。
と言っても、科学的方法に則って検証するために、仮説から何が予言でき、観察できればいいのかを考えてみます。
この仮説から予言できる結果は、「ボールに与える力が大きいときには、ボールの速さは速い」ことと「ボールに与える力が小さいときには、ボールの速さは遅い」となります。
| (25.1)次の仮説が正しいと証明するために、結果として観察されるべき事実の予言は何か [仮説] ボールの速さは、加える力の大きさに依存する <予言> ボールに与える力が大きいときには、ボールの速さは速い <予言> ボールに与える力が小さいときには、ボールの速さは遅い |
そして、実際に実験をしてデータをとります。ボールを全力で投げる場合の速さと、ボールを軽く投げる場合の速さのデータを実験して集めます。
(補足:講義中は柔らかいボールを実際に投げて示した)
そうすると、予言「ボールに与える力が大きいときには、ボールの速さは速い」ことと「ボールに与える力が小さいときには、ボールの速さは遅い」ことが観察されます。
これで、仮説が正しいことが証明できました。
これは、ボールの速さや力の入れ方は直接観察できますし、特段困ることはありません。ただし、実際に科学的に行う場合には、加える力や速さを厳密に測定する必要があります。ここでは、そのような測定器材がないので、説明の便宜上、そこまではしていません。
では、第 I 部 論理的思考 第6章 仮説思考 4 演繹法による予言 観察可能な事実で使った事例である(6.2)を思い出してください。
| (6.2)次の仮説推論の検証方法は何か <前提1> 海辺が近くない陸地で魚の化石が発見された (観察事実=小前提) <前提2> この一帯の陸地は昔海であったならば、海辺が近くない陸地で魚の化石が発見される(大前提) [結論] よって、この一帯の陸地は昔海であった (仮説) |
「この一帯の陸地は昔海であった」という仮説は、タイムマシンで過去に行けるのならば別としても、今現在の科学の力では、どうやっても直接観察できません。ですから、仮説から予言される結果を、間接的に観察できないかと考えます。
この間接的に観察するためには、何かが存在するならば、それに付随する要素も存在する、ということを利用することになります。
以前の説明と同じですが、日が射したとき、そこに人が立っていれば影ができます。背後に人がいるか確認しなくてもその影が確認できれば、そこに人が立っていることが分かるものです。この場合、「何かが存在するならば、それに付随する要素も存在する」とは、「人」が存在すれば、それに付随する要素である「影」も存在するということです。振り向けない等の条件によって「人」を直接観察できなくても、「影」を観察できれば、間接的に「人」が存在することが分かる、ということです。
つまり、「この仮説が正しい⇒当然に生じるであろう、あの事象・事実が観察できる」という論理です。
そこで、この仮説から予言されることは、前提1(観察事)の「海辺が近くない陸地で魚の化石が発見され」ることです。
ただし、「1つ」だけではなく、「多くの魚の化石」の発見が必要です。1つだけでは偶々陸上生物が海辺で魚を丸呑みして、陸地に移動して来て消化前に死んで化石化したということも考えれらます。そのような偶然が起こったとは考えることが難しいほどに、「多くの魚の化石」が発見されればいいわけです。
このように考えれば、「この一帯の陸地は昔海であった」ことが直接観察できなくても、「多くの魚の化石」の有無を調べることで、間接的に観察できることになります。
後は、発掘調査を重ねて、データを集めます。
実際に「多くの魚の化石」が見つかれば、仮説が正しかったことが分かります。
逆に「多くの魚の化石」が見つからなければ、仮説が誤りだったことが分かります。
このように、仮説を検証する際には、観察可能な事実が何なのかを考えないといけません。
特に、観察すべき対象が目で直接確かめることができないような場合は、この観察可能な事実が何なのかということを、かなり深く考える必要が出てきます。
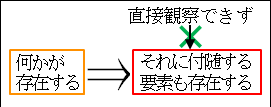
そして、今まで観察可能な事実と呼んで来たもの、つまり、何かが存在するならば、それに付随する要素も存在するという前提の下に、観察されることが当然に予測される具体的な事実は、観察可能な含意と呼びます。
したがって、観察可能な含意は、存在する「何か」です。その観察された「何か」が、観察されていない「それに付随する要素」を含んでいると解釈できる、ということになります。
観察可能な含意は、英語では observable implications と言います。
「観察する」という意味の observe と、「可能」を表す接尾辞 -able で、observable となり、「観察可能な」となります。
そして、implications とは「明確には述べられていないが、導出できる見解」といった意味であり、日本語でいうところの「含意」になります。「含意」とは、「明確に述べられていないが、引き出し得る意味」ということです。
この観察可能な含意という用語は、主に政治学や経済学、心理学といった社会科学で使われます。事実というよりは「含意」として観察することになります。
「何かが存在するならば、それに付随する要素も存在する」という前提の下に、実際に観察されるものは、存在する「何か」であり、「それに付随する要素」は観察されません。
図25.5.観察可能な含意
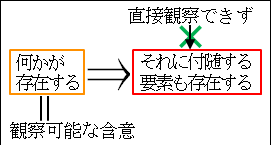
それなのに、実際には観察されていない「付随する要素」が、まるで実際に観察されたかのように扱われるのは、観察された「何か」が観察可能な含意だからです。
図25.5.観察可能な含意
このように、観察された「何か」によって、観察されていない「それに付随する要素」を含んでいると解釈できる、ということになります。
こうして、観察可能な含意を観察することで、「付随する要素が存在する」ことも証明できたと考えられます。
図25.5.観察可能な含意
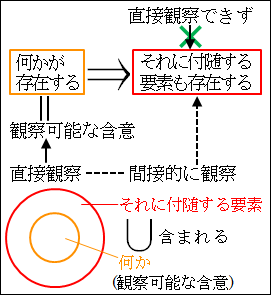
このように、観察された事実から、明確に観察されていないことを引き出しているので、観察可能な事実と呼ぶよりは観察可能な含意と呼ぶ方が相応しいでしょう。
そして、観察可能な含意として、観察されていない「それに付随する要素」を観察されたと解釈するために、「何か」を観察するとき、自然科学ならば、最終的に物体や物質など確固として存在するものに遡ることができる場合が多いです。
実際、「魚の化石の発見」から「現在の陸地が昔海であった」と解釈する場合でも、「魚の化石」という実際に存在するものが観察されているので、論理的に飛躍が少なくすむため、仮説や理論としてあまり無理がありません。
地層や化石の形成の仕方は、モデルで明らかになっています。そのモデルを前提に、ある一帯で化石が大量に発見されれば、その観察された事実から、当然に付随する要素も存在すると考えても無理がないからです。ですから、実際に肉眼で確認できなくとも、現象が存在する、あるいは、存在したことを、何か(多くの魚の化石)が存在すれば、付随する要素(昔海だった)が存在すると推論できます。
このように、自然科学は、観察可能な含意によって間接的に観察している場合でも、元々の始まりは直接観察した事実を基に出発していることが多いです。
それに、直接観察できず間接的に観察するしかない場合でも、どうやってもそう考えるしかない、といった状況になるまで色々と実験をしていることが多いです。
ですから、観察可能な含意が解釈問題になることは少ないです。
が、しかし、社会科学はそうはいきません。それは、社会科学の研究対象が人間の社会や制度であり、目に見えず直接観察できる事実が少ないからです。つまり、間接的に観察する以外に方法がない場合がかなり多いのです。
直接観察できるものから論理を出発できないかと、どんどん根拠と論理を遡って行っても、実際に観察されたものではないものから出発していることが普通にあります。
また、自然科学のような実験もできないことが多いです。現実の社会や人間関係の条件の1つだけを何回も変えてデータを取るようなことが果たしてできるでしょうか。
このように、間接的に観察したと言っても、「含意」から仮説を導く解釈は、皆が納得するような形になっていないことが多いです。
ですから、社会科学の場合には、仮説を証明するために必要な予言の観察について、自然科学以上に観察可能な含意を上手く定義して導き出しておかないと、使い物にならない仮説ばかりになります。
さて、直接観察できる観察事実と、間接的に観察するしかない観察可能な含意があることが明らかになりました。
そこで、予言や観察可能な含意を上手く導き出して定義するために、概念的定義と操作的定義という2つの考え方を学びます。
概念的定義は、日常的な意味での「定義」と似ています。要は、「A は~である」といった言葉による定義になります。
概念の意味は何でしょうか(第8章 観念連合 2 観念・概念・範疇参照)。覚えていますか?
概念とは、事物の本質や特徴を捉えて、明確に言語化した考えという意味です。
したがって、概念的定義は、事物の本質や特徴を捉えて、明確に言語化した考えの定義と言えます。英語では、conceptual definitions と言います。
何よりもまず概念的定義によって、理論やモデルは説明されます。
私達は言葉を使って思考をするので、使う言葉の意味、つまりは定義がしっかりされていないと、会話ができません。このように、概念的定義が設定されることで、物事が何を意味しているのかが理解できるようになります。
したがって、概念的定義は、対象を分析して本質や特徴を捉えるため、論理的に推論し抽象化しながら言葉で記述して作りだします。
しかし、概念的定義は、事物の本質や特徴を捉えた定義なので、どうしても抽象的で一般的になってしまいます。
いくら科学では概念的定義に従って考察するといっても、定義が抽象的で一般的であると、データを集めたり実験したりするとき、対象が無闇に広くなり過ぎたり、許容される行為が曖昧になりがちになります。これは、実際に具体的なデータ収集と実験を行う上で困ったことになります。
このように、概念的定義は意味を理解し把握するのに使えますが、具体的に分析するには抽象的過ぎます。
そこで、データ収集や実験がしやすいように、より扱いやすい具体的な定義が欲しくなってきます。このとき、使えるのが操作的定義です。英語では、operational definitions と言います。
操作的定義とは、直接測定できない対象を測定可能な形式に変形した定義です。
つまり、操作的定義は、何を観察すればいいのか曖昧な抽象的な概念的定義を、観察できる具体的な形式に変形した定義と考えることができます。
科学で実際に何かを調べたり実験したりするとき、抽象的な概念的定義では、何を観察したらいいのかが不明瞭なので、観察対象を具体化したいと考えます。
そこで、抽象的な概念的定義を、具体的な操作的定義に落とし込みます。
こうして、抽象的な概念的定義は、操作的定義として具体化されることになります。
そして、抽象的な概念的定義は、具体的な操作的定義を観察することで、間接的に観察され証明されます。
このことから、操作的定義は、概念的定義を扱えるように、うまく操作して具体的に定義し直したものだと分かります。
まさに、操作的定義は、操作された定義です。
抽象的な概念的定義に対して、それを具体的にした操作的定義という関係性は、抽象と具体の関係にあることになります(第4章 演繹法 2 一般・普遍・抽象と個別・特殊・具体参照)。
抽象と具体との関係においては、抽象的な概念A は、具体的な概念A1、A2、A3、…に具体(具象)化できます。逆に、具体的な概念A1、A2、A3、…は、抽象的な概念Aに抽象化できます。
そして、抽象的な概念A には、具体的な概念A1、A2、A3、…に共通する性質 a が存在します。
逆に、具体的な概念A1、A2、A3、…には、共通する性質 a 以外にも、それぞれが様々な要素b、c、d、…が存在します。
図4.1.抽象化と具体化
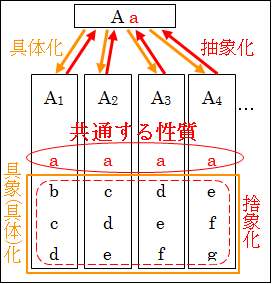
概念的定義と操作的定義は、まさに抽象と具体の関係にあります。
図25.6.概念的定義と操作的定義
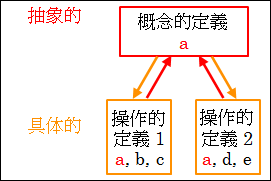
1つ1つの具体的な操作的定義は、共通する性質とそれぞれに特有の要素を持っています。
その共通する性質を抽象化した概念的定義は、その意味の通り、事物の本質や特徴を捉えて、明確に言語化した考えの定義だというのが分かります。
この抽象的な概念的定義は、直接観察するのが難しいです。ですから、具体的な操作的定義を観察することで、間接的に抽象的な概念的定義を証明します。
図25.6.概念的定義と操作的定義
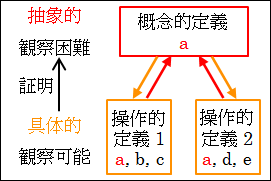
そして、操作的定義が、実際にどのような状態や状況であるのかを表すのがデータになります。
図25.6.概念的定義と操作的定義
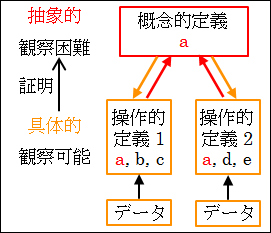
このデータは、操作的定義よりもさらに具体的なものです。
つまり、データは確固とした物質や事実、統計の数字や資料であることがほとんどです。
したがって、解釈が分かれ得る抽象的な概念的定義と異なり、データ自体には解釈の余地は生じないのが原則になります。
少し難しかったでしょうから、繰り返しになりますが、概念的定義とデータの間を操作的定義が繋げていることをまとめて整理しておきます。
概念的定義は抽象的です。
操作的定義は具体的です。
データはさらに個別的で具体的になります。
概念的定義を見るだけでは、意味は何となく分かるけど、何のデータを集めればいいのかが、曖昧です。
逆に、データを見ているだけでは、そのデータが何を意味しているのかが分かりません。
そこで、概念的定義とデータの間を繋ぐのが、操作的定義です。
操作的定義は、概念的定義をより具体化して、測定できる形式に変形した定義です。
したがって、操作的定義は、概念的定義に従って調べたり集めるべきデータが何なのかを示していることになります。
同時に、操作的定義は、そのデータが意味している解釈つまり概念的定義が何なのかを示していることになります。
以上をまとめると、次のような論理になっているのが確認できました。
概念的定義自体は抽象的なので、直接観察するにしても、何を観察したらいいのかが曖昧である。
したがって、具体的な操作的定義を通じてデータを観察することで、概念的定義を観察したことにする
こういった論理です。
このことから、操作的定義は観察可能な含意と同じ意味であることが理解できます。
図25.6.概念的定義と操作的定義
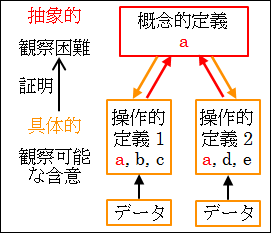
後は、操作的定義つまり観察可能な含意が存在することを、さらに具体的なデータや事実を集めて行けばいいのだと分かります。
例えば、「経済格差が拡大している」ということについて考えてみましょう。
| (25.2)経済格差が拡大しているという仮説を証明するために必要な操作的定義(観察可能な含意)は何か |
概念的定義は、「経済格差の拡大とは、貧富の差が広がっていることである」とできます。
| (25.2)経済格差が拡大しているという仮説を証明するために必要な操作的定義(観察可能な含意)は何か [概念的定義] 経済格差の拡大とは、貧富の差が広がっていることである |
では、「貧富の差が広がっている」ってどうやって観察すればいいのでしょうか。
新聞で報じられている貧しい人の声でも拾ってきて、証明しますか?
でもそれは、貧しい人個人の貧しい生活であって、多くの人がそうだとは限りません。
個別的で具体的な1つの事例を簡単に一般化するのは科学的ではありません。
このように、概念的定義の段階では、何を調べたり観察したらいいのかが曖昧です。何を観察しても「貧富の差が広がっている」ことに結び付けられそうです。
そこで、操作的定義として、「人口に占める貧困層の割合が増加している」や「国全体の富に占める富裕層の割合が増加している」などと具体化します。
| (25.2)経済格差が拡大しているという仮説を証明するために必要な操作的定義(観察可能な含意)は何か [概念的定義] 経済格差の拡大とは、貧富の差が広がっていることである <操作的定義> 人口に占める貧困層の割合が増加している <操作的定義> 国全体の富に占める富裕層の割合が増加している |
そうすると、これらの操作的定義に当てはまるデータを集めて、分析すればいいのだと分かります。
具体的には、抽象的な概念的定義「経済格差の拡大とは、貧富の差が広がっていることである」については、その具体的な操作的定義「人口に占める貧困層の割合が増加している」と「国全体の富に占める富裕層の割合が増加している」から、その操作的定義のさらに個別的で具体的なデータを集めることで、正しいかどうかを判断できるようになっています。
仮に、「人口に占める貧困層の割合が10年にわたって上昇している」とか「国全体に占める富裕層の割合が10年にわたって上昇している」といったデータが取れれば、操作的定義を通じて、概念的定義である「経済格差の拡大とは、貧富の差が広がっていること」が正しいことを証明できたと言えます。
ここで、注意点があります。
概念的定義を説明するために操作的定義を用いているということは、抽象的な概念的定義は、具体的には操作的定義になるということを心に留めておかないといけません。
仮に、具体的な操作的定義を無視して、抽象的な概念的定義だけを取り上げてしまうと、理論やモデルが説明できる現象の範囲を簡単に逸脱してしまいます。
例えば、先程の例である「経済格差が拡大している」で考えてみましょう。
概念的定義「経済格差の拡大とは、貧富の差が広がっていることである」ことが、2つの操作的定義「人口に占める貧困層の割合が増加している」と「国全体の富に占める富裕層の割合が増加している」を通じて、データを集めることで証明できたとします。
そうすれば、このとき、概念的定義「経済格差が拡大しており、貧富の差が広がっている」という前提の下に色々と考えることができるでしょう。
しかし、あくまで、2つの操作的定義「人口に占める貧困層の割合が増加している」ことと「国全体の富に占める富裕層の割合が増加している」という意味において、概念的定義「経済格差が拡大しており、貧富の差が広がっている」ことに留意しなければなりません。
概念的定義「貧富の差が広がっている」の中に含まれていない具体的な内容、例えば「貧困層の貧困度合いが増している」といったことを勝手に導き出して証明されたもののように扱うことは、慎まないといけません。
証明されたのは、操作的定義である「人口に占める貧困層の割合が増加している」ことと「国全体の富に占める富裕層の割合が増加している」という意味においての概念的定義である「貧富の差が広がっている」ことです。
それなのに、概念的定義「貧富の差が広がっている」という定義に引っ張られて、証明されていない「貧困層の貧困度合いが増している」ことまでも証明済みのものとして扱うのは、真偽不明の前提を用いていることになり、論理的な主張の説得力を下げてしまいます。
またさらに、真偽が不明だということは、偽の可能性もあるわけです。もし誤った前提に立って論理を組み立てると、論理的な主張としての価値がなくなってしまいます。
故意にしろ過失にしろ、抽象的な概念的定義の字面に引っ張られて、具体的な操作的定義の内容を無視して、都合の良いように概念的定義の内容を捻じ曲げてしまうことが、ままあります。
皆さんも概念的定義だけではなく、操作的定義が何なのかを気にするようにしてください。そして、該当する概念的定義に含まれていない具体的な要素を扱うときは、証明を別にするなどして注意が必要なことを肝に銘じておいてください。
こうしたことからも、議論するときに、物事の定義を明確に宣言しながら進めることが大切なのが分かります。定義を曖昧にしていると、話が簡単にそれたり、論理的に問題が生じることが大変多いです。
なお、いわゆる理系の学問である自然科学では、概念的定義と操作的定義の乖離が少なく、無理矢理解釈しなくても、納得行くものになることが多いです。
しかし、いわゆる文系の学問である社会科学や人文科学では、概念的定義と操作的定義の乖離があり、解釈が人によって異なることが多いです。
これは自然科学が、条件を制御して、実験を積み重ねることができるのに対して、社会科学や人文科学ではそうした実験を行うことが難しいため、定義を定めることが難しいからだと言えます。
▼雑談を飛ばす
これを踏まえると、世間でよく言われる「理系は定義に煩い」といった言説は、奇妙なことに気付きます。皆さんも、理系は「その定義は何なのか?」と定義を細かく訊いて来るみたいな話を耳にしたことがあるかと思います。
しかし、本来なら、文系の方が、定義について争うことが多くなる傾向があるはずなのが私見です。これは世間の認識とは逆ですね。でも、仮に、定義を気にする度合いに文理で差がつくことが事実なのだとしたら、私としては、理系よりも文系の方が定義に敏感になる傾向が強くなるのが本来の姿だと思っています。
まず、理系の方が、学問の中で用語に対する定義が、皆がそうだと納得するキッチリとした形でなされていることが多く、定義がどうだこうだと問題になることが少ない気がします。
ですが、文系の方は、同じ専門分野にもかかわらず、使う人によって定義が違っていることが多く、そのため定義が曖昧になりがちです。話す度に定義をしっかりとしていかないと、反対するにしろ賛成するにしろ、話が噛み合わないことに陥ることが多い気がします。
ですから、もし文系と理系で定義に敏感になる度合いが本当に違うのだとしたら、文系の方がより敏感になる傾向が強いのだと思うのです。
と言っても、文系や理系で分けること自体が、あまり意味のあることだと思わないですし、所詮印象論みたいな言説でしょうから、どうでもいい話ではありますが。こう思ったわけです。
ちなみに、私の仮説ですが、いや検証も何もしていないので妄想と言った方がいいかもしれませんが、なぜ理系の方が定義に煩いという印象があるのかについての分析があります。
本来なら、文系だろうが理系だろうが関係なく、大学生なら科学的思考ができるようになっているはずなので、定義の大切さを知っているはずです。ですから、本来的な意味での大学生ならば、定義についての煩さに、文理で差がそこまで出るはずがありません。
それなのに、「理系は定義に煩い」という言説が流れているのは何故でしょうか。
実は私は、この言説を、友人が持っていた「理系男子との付き合い方」みたいな恋愛系の記事で目にしました。まぁ何とも頭の悪そうな記事だと偏見を持ちながら目を通したのですが、そこから考えた私なりの説明がこうです。
まず、日本の大学の悲しい所ですが、文系はあまり勉強しません。バイトやサークル等で忙しいですし、ろくに勉強せずとも卒業できます。勉強しないのだから、今説明している科学的思考がどういったものなのかも理解していない、あるいは、使いこなせない人が多くなります。これは高校生の人にはピンと来ないかもしれませんが、そういった状況になっています。
一方で理系は、実験に忙しく、レポートが大量に出され、科学的方法を身に付ける努力をしないと卒業できません。そうすると理系は、文系に比べて、科学的思考で物事を考える癖がつく人の割合が多くなってしまいます。
こうして、現状の日本の大学では、科学的思考をする理系に対して、科学的思考を心得ない文系という図式ができてしまいます。
次に、現代日本の大学進学状況を考えると、理系に進学するのは、男子が主です。女子の多くは、文系に進みます。これは事実ですね。
したがって、理系に男子が多く進み、文系に多くの女子が進むので、理系男子と付き合う女子は、必然的に文系が多くなります。
先に説明したように、文系の多くは男女に関係なく科学的思考が苦手なので、文系女子の多くも科学的思考ができません。そうすると、身分は大学生あるいは大卒なのに、話している内容や論理の組み立て方が高卒程度と大差がなくなってしまいます。
これでは、科学的思考ができる理系男子からしたら、科学的思考をしない文系女子の話は、何だか感覚的で曖昧に感じられ、非常に主観的過ぎて、共感しようにも、まず理解ができないことになります。自分がそう考えていること、つまり、主観は、自分だけにしか分かりません。相手に理解してもらうには、完全ではないにしろ、皆がそうだと考えられる客観性が必要になります。
もちろん、口だけで「そうなんだ、分かる」と別に言ってもいいのですが、実の所分からないので、衝突も増えるでしょう。それに相手の言いたいことが分からないのに分かったと言うのは不誠実に思えるので、ついつい「定義をしっかりしてくれ」と言ってしまうものです。
逆に、科学的思考をしない文系女子にとっては、科学的思考をする理系男子が定義について煩く感じるようになるはずです。
ここにいる皆さんは高校生も多いので、ピンと来ないかもしれません。言ってみれば、今、高校生であるあなたが、小学生あるいは中学生と話して、思慮が浅いと感じずに話すことができますか? ほとんどの人は、相手の知識の多い少ないだけではなく、論理的思考の未熟さに苦労させられるはずです。
科学的思考ができる人と、科学的思考ができない人はこれと似たような状況になります。
このようにして、理系男子は定義に煩いという言説が生まれているのではないでしょうか。ですから、この言説からは、「理系は定義に煩い」とかいう下らない情報ではなく、もっと有益な情報として、実は「日本の大学の文系学部の生徒の質の低さ」を読み取ることができます。もっと厳しく言えば、科学的思考ができない文系は、文系ですらない何か、大学生未満として区別すべきでしょう。そうでないと、真面目に勉強して科学的思考を身に付けている数少ない本物の文系学生が可哀そうです。
まぁ所詮、これは、実態調査も検証もしていない私の経験や印象から導いており、くだらない記事に対する与太話、あるいは笑い話や冗談なので真に受けないでください。
▲雑談に戻る
5 変数
概念的定義と操作的定義について理解できたでしょうか。
操作的定義は、抽象的な概念的定義についての具体的な定義であり、それは変数となります。英語では、variables です。vary が「変わる」という意味で、接尾辞の -able が「可能」を表すので、vari-able で、「変わることができるもの」ということを意味します。
ですから、変数とは、対象の本質や性質に関係づけられた論理の集まりです。
もっと簡単に言えば、変数は自由に変化することができる要素や特徴です。
なお、variables の日本語訳が変数であるため、変数の「数」という字面から、1、2、3、…といった数字を思い浮かべ、数字が変わることだと考えるでしょうが、必ずしも数字に限らず変わる要素や特徴といった少し広い意味で捉えておいてください。
この変数は、数学で馴染み深い考え方かと思います。
X や Y が変数で、Y=X などと書いたりしますね。変数X に、1や2を入れたりしますが、その変数に入れられる値のことを変数値と言います。英語では、valuesです。
さて、Y=X と書いたりするとき、この X と Y の関係は、X の値が変化すると、それに応じて Y の値も変化するという関係になります。
数学では、Y の値をいじって、X がどう変化するかといったことを調べたりすることもありますが、ここでは説明の便宜上、変化は X から Y への一方通行で考えます。
つまり、X が変化したら Y が変化するのであって、Y が変化したら X が変化するわけではありません。
図25.7.変数と変数値 
このとき、X と Y の間には因果関係を見て取れます。
X が原因で、Y が結果になります。
図25.7.変数と変数値 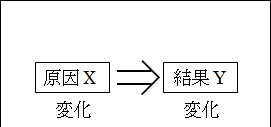
そして、原因たる変数X は独立変数と言い、結果たる変数Y は従属変数と言います。
何故このような呼称になっているかは簡単です。原因である独立変数X が先に変化して、それに応じて結果である従属変数Y が変化するからです。つまり、
X は、何も影響を受けず独立に変化する要素なので、独立変数です。英語では、independent variables と言います。
Y は、独立変数X が変化したことに従って変化する要素なので、従属変数です。英語では、dependent variables と言います。
図25.7.変数と変数値 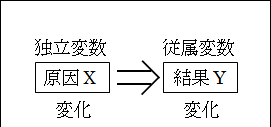
「X が変化する ⇒ Y が変化する」のだから、原因である独立変数X の変数値が変われば、結果である従属変数Y の変数値も変わります。
つまり、原因である独立変数X の変数値xnが変化することで、それに従って結果である従属変数Y の変数値ynも変化することになります。
図25.7.変数と変数値 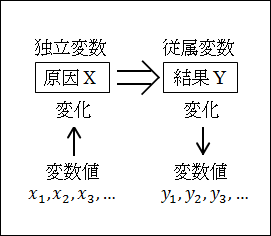
原因である独立変数X の変数値が x1 のときには、結果である従属変数Y の変数値は y1 になります。
原因である独立変数X の変数値が x2 のときには、結果である従属変数Y の変数値は y2 になります。
原因である独立変数X の変数値が x3 のときには、結果である従属変数Y の変数値は y3 になります。
図25.7.変数と変数値 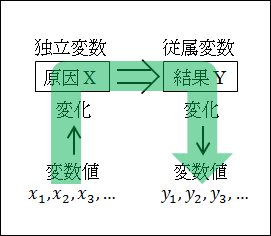
このように、原因である独立変数X の具体的な内容である変数値xnが変化することで、結果である従属変数Y の具体的な内容である変数値ynが決まります。
因果関係については、第10章 論理的思考のまとめ 4 因果関係と相関関係について詳しくやったので、よく復習しておいてください。
図10.5.相関関係から因果関係の特定 
それでは、操作的定義が変数であることの意味を考えてみましょう。
操作的定義は、抽象的な概念的定義を具体化して、調べる必要のある具体的なデータが何なのかを表していました。
ですから、操作的定義は、調べたデータによってその具体的な内容がコロコロと変わることになります。
つまり、操作的定義は、その具体的な内容が「変わる」ことになります。まさに変数です。
図25.7.変数と変数値 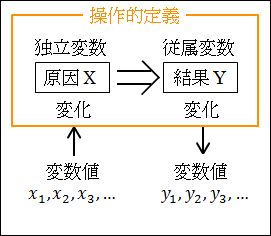
そして、実際に調べられる具体的なデータは、操作的定義たる変数に入れられる具体的な値です。
つまり、具体的なデータは、まさに変数値です。
図25.7.変数と変数値 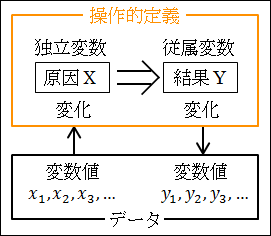
このように、操作的定義によって、変数として何を具体的に調べればいいのかが分かり、変数がどのように変わっているかを示す変数値はデータとして現れます。
したがって、実際に観察するのはデータになります。
以上のように、操作的定義が変数であり、具体的なデータが変数値だということが分かりました。
例えば、(25.1)の「ボールの速さは、加える力の大きさに依存する」という仮説に戻って考えます。この仮説とそれから導かれた予言のいずれが、概念的定義で、操作的定義なのかを考えます。
| (25.3)(25.1)の仮説と、その仮説を正しいと証明するために結果たる予言において、概念的定義と操作的定義がどれかを指摘せよ。また、操作的定義において、独立変数と従属変数が何かを指摘せよ [仮説] ボールの速さは、加える力の大きさに依存する <予言> ボールに与える力が大きいときには、ボールの速さは速い <予言> ボールに与える力が小さいときには、ボールの速さは遅い |
今回はこの仮説がそのまま概念的定義になります。
この仮説の予言は、「ボールに与える力が大きいときには、ボールの速さは速い」ことと「ボールに与える力が小さいときには、ボールの速さは遅い」でした。
この2つ予言が操作的定義となりす。
| (25.3)(25.1)の仮説と、その仮説を正しいと証明するために結果たる予言において、概念的定義と操作的定義がどれかを指摘せよ。また、操作的定義において、独立変数と従属変数が何かを指摘せよ [仮説] ボールの速さは、加える力の大きさに依存する(=概念的定義) <予言> ボールに与える力が大きいときには、ボールの速さは速い(=操作的定義) <予言> ボールに与える力が小さいときには、ボールの速さは遅い(=操作的定義) |
そして、この2つの予言は、2つの同じ変数によって説明できることに気付きます。
原因である独立変数X が、ボールも与える力とします。
結果である従属変数Y が、ボールの速さとします。
図25.8.変数と変数値の例
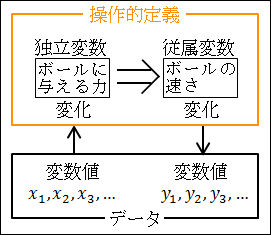
そして、原因である独立変数X・ボールも与える力の変数値は、実験で実際にボールに与える力の大きさになります。
結果である従属変数Y・ボールの速さの変数値は、実験で実際に記録されるボールの速さになります。
原因である独立変数X の変数値、すなわち、ボールに与える力の大きさを変えて、何度も実験を試みて、その都度、結果である従属変数Y の変数値、すなわち、ボールの速さを記録します。
このように、2つの予言である「ボールに与える力が大きいときには、ボールの速さは速い」ことと「ボールに与える力が小さいときには、ボールの速さは遅い」ことは、1つの操作的定義の形式「ボールに与える力の変化⇒ボールの速さの変化」にまとめることができました。
| (25.3)(25.1)の仮説と、その仮説を正しいと証明するために結果たる予言において、概念的定義と操作的定義がどれかを指摘せよ。また、操作的定義において、独立変数と従属変数が何かを指摘せよ [仮説] ボールの速さは、加える力の大きさに依存する(=概念的定義) <予言> ボールに与える力が大きいときには、ボールの速さは速い(=操作的定義) <予言> ボールに与える力が小さいときには、ボールの速さは遅い(=操作的定義) 独立変数:ボールに与える力 従属変数:ボールの速さ ボールに与える力の変化⇒ボールの速さの変化 |
この例からも、操作的定義が変数の集まりであることが分かったかと思います。
なお、対照実験でも説明しましたが、独立変数X と従属変数Y の関係だけに注目していることから、独立変数X の変数値以外の条件は一切変えないのが原則になります。
つまり、原則として、1回の実験で、変数の中で変えてもよいのは独立変数X の1つのみです。
図10.4.対照実験
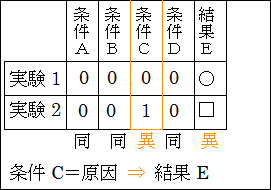
仮に他の変数Z も一緒に変わっていたとしたら、変数X と Z のどちらが、Y の変化をもたらしたか分からなくなってしまうからです。
変えていいのは、注目している独立変数X だけだということを肝に銘じておいてください。
ですから、実験やデータの収集ができるように、上手く変数を制御 control できるような定義や環境を整える必要があります。
そして、いわゆる理系の学問では、実験室等で条件を制御して厳密に実験できることが多いのに対して、いわゆる文系の学問では、そうはいかないことが多いです。
社会の状況を1つの変数以外すべて同じにすることなど到底できません。まったく同じ状況は2度とは現れません。
何か経済理論の仮説を形成できたとして、それが本当に正しいのかを自然科学並みに変数を制御して検証するための実験はできません。そんなことができるとしたら、私達の社会の自由は徹底的に統制されてしまいます。さらに失敗した場合に、どれほどの影響がでるかも未知数です。実験の結果、とんでもない悲惨な状態になり得ることもあるわけです。
以上のために、社会科学の仮説検証は厳密には困難で、理論やモデルを自然科学の法則のように考えてはいけなません。
これが、人間の文化や精神性や歴史の解明とかになると、もっと難しいことが容易に想像できます。
人間は経験と共に変化します。その変化は不可逆的、つまり、二度と前の状態には戻れません。一度経験したことを忘れて、同じ経験をしたら、どうなるのかは試しようがありません。
また、歴史でも、史料や遺跡等が残っているので、何かがあったことは分かります。変数値がそうした史料や遺跡等にあたります。そうした「事実」を積み重ねて歴史を明らかにしていきます。しかし、歴史を再現しようにも、時代背景も価値観も、生きている人もあまりにも違い過ぎます。したがって、実験ができるかと言ったときには、まず無理です。「もし~だったら、どうなっていただろうか」や「もし~でなかったら、どうなっていただろうか」といったことは、変数を制御して実験のしようがないので、本当にそうだったのかは検証のしようがありません。想像の域を出ません。
このように、自然科学に比べて社会科学や人文科学は、有効な仮説検証ができないことは、しっかりと理解しておいてください。
最後に補足として付け加えておくと、独立変数のことを説明変数、従属変数のことを被説明変数と呼んだりすることもあります。
説明変数(独立変数)が被説明変数(従属変数)を「説明する」ためです。
また、独立変数が直接、従属変数に影響を与えるのではなく、その間に異なる変数が入っていることもあります。
このとき、独立変数と従属変数の間を繋ぐ変数のことを媒介変数と言います。
「媒介」が「両方の間に立って、仲立ち・仲介すること」という意味です。
| 独立変数⇒媒介変数⇒…⇒従属変数 |
独立変数と従属変数の間を繋ぐ変数である媒介変数が1つとは限らず、独立変数と従属変数の間を複数の媒介変数が介在することもあります。
そうすると、因果関係がどんどん伸びてい行くことになるので、論理的に本当に繋がっているのかについて、いつも以上にしっかりと確かめないといけません(第20章 論理ピラミッド 5 注意点参照)。
なお、媒介変数は、英語では parameters と言います。日本語でも媒介変数ではなく、カタカナでパラメータと言ったりすることが多いです。
6 まとめ
以上で科学的方法について学びました。長くなったので、重要事項をまとめておきます。
科学的方法は、観察―仮説形成―仮説検証の循環をグルグルと回りながら行われました。
図25.9.科学的方法と理論 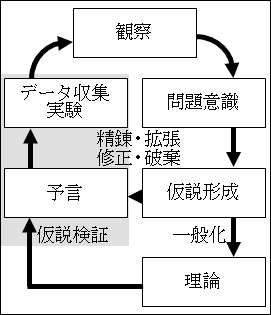
まず、対象を観察します。
そうすると、どうしてこうなっているのだろうか等といった問題意識を持ちます。
そこで、その問題意識に対しての合理的な説明である仮説を形成します。
仮説が形成できたら、その仮説が正しいかどうかを確かめるために検証します。
仮説が正しいとしたら、結果としてどうなるか、という予言をします。
その予言が実際に観察できるか、データ収集をしたり実験をします。
予言の通り観察できれば、仮説は正しいと言えます。予言の通りに観察できなければ、仮説は正しくないことになります。
そして、また観察に戻ります。データや実験の結果などを観察したことから、新たに問題意識を持ち、仮説を精錬・拡張、修正・破棄していきます。
仮説が証明されて、色々と分かってきたら、物事を法則的・統一的に論理的に説明するために、理論を作ります。
つまり、1つまたは複数の仮説を一般化します。こうして形成された理論も、仮説なので、実際に正しいか仮説検証して正しいことを証明する必要があります。
このような手続きの循環が科学的方法の大枠となります。
この手続きを踏むことが、学問的である・科学的であるということを意味します。
それでは、前章と合わせて、学問と科学の定義を改めて確認しておきます。
学問と科学の定義は、「一定の目的と方法の下に行われる、様々な事象の研究活動であり、その研究活動によって得られる知」でした。
そして、「一定の目的」は「真理の追究」を意味しました。したがって、具体的には、
| 学問・科学とは 今現在における、より正しいとされる物事・事柄・筋道を明らかにするために、一定の方法の下に行われる、様々な事象の研究活動、および、その研究活動の成果として得られる知識、その知識の体系や理論 |
となりました。
そして、今回学んだ学問的方法あるいは科学的方法が、「一定の方法」でした。したがって、「一定の方法」とは、「観察―仮説形成―仮説検証という科学的方法の手順に則る」と言えます。これを踏まえると、
| 学問・科学とは 今現在における、より正しいとされる物事・事柄・筋道を明らかにするために、観察―仮説形成―仮説検証という科学的方法の手順に則って行われる、様々な事象の研究活動、および、その研究活動の成果として得られる知識、その知識の体系や理論 |
と定義できます。
そして、科学的方法の手続きに則って仮説や理論を形成する場合、モデルで考えることが大切になります。いわゆるモデル思考です。
図25.10.モデル(理論)思考 画像クリックで拡大
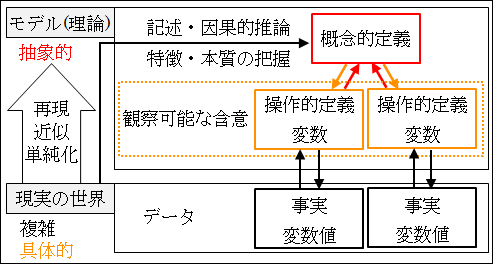
現実の世界の事象は、複雑で理解するのが難しいです。
そこで、複雑で理解困難な対象を理解するために、その本質や特徴を単純化して近似して再現したモデルを作ります。
そして、モデルを作るとき、概念的定義と操作的定義を明確にすることが大切になります。
まず、現実の世界にある対象の特徴と本質を記述します。この事物の本質や特徴を明確に言語化した定義が、概念的定義になります。
このとき、対象を論理的に推論しながら、本質や特徴を記述しないといけません。また、因果関係が見つかりそうな場合は、その因果関係も論理的に推論します。
しかし、概念的定義は、本質や特徴を抜き出しているので、非常に抽象的です。つまり、モデルから導かれる仮説が抽象的になり、具体的に何を観察して検証すればいいのかが曖昧になります。
そこで、概念的定義を操作的定義に具体化してあげます。操作的定義とは、直接測定できない対象を測定できる形式に変形した定義でした。
この操作的定義が観察されれば、概念的定義が観察できたという解釈できます。
ですから、操作的定義は観察可能な含意と言えます。
また、操作的定義が概念的定義を具体化したものであり、事物の本質や特徴を明確に言語化した定義を測定できる形式に変形して具体化した定義を意味することから、操作的定義は、対象の本質や性質に関係づけられた論理の集まりと言えます。
これが測定できるものだから、変数と考えることができます。
そして、変数は、そのより具体的な値として変数値を持ちます。
変数値が変わると、変数の結果も変わります。
何にも影響を受けず独立に変化する変数を独立変数、その独立変数の変化に従って変化する変数を従属変数と言いました。独立変数は説明変数、従属変数は被説明変数と呼ばれることもあります。
また、独立変数と従属変数との間に変数が介在する場合は、その間にある変数を媒介変数と呼びました。
変数値は、変数の具体的な値ですから、変数である操作的定義よりもさらに具体的なもの、つまり、データになります。
したがって、実験や情報収集はこのデータたる事実を変数値として扱うことになります。
変数値であるデータを観察することで、変数である操作的定義の具体的な内容が決定され、そこから概念的定義が実際にどうなっているのかが明らかになります。
このようにしてモデルを組み立てて使うことで、理解困難な現実を近似して理解することができます。
論理的思考を用いて意見を主張したり問題を解決をするとき、結論を導くための根拠たる前提に科学的知識を正しいものとして使える理由は、このような科学的方法によって証明されていることに求められます。
「何でか分からないけど、学校でそう習ったし正しいのだろう」という認識ではなく、こうした手続きを経て正しいものとして認められるようになったことをしっかりと意識してください。
そして、この手続きが科学的方法であるため、この科学的方法による正しいことの証明には弱点あるいは欠点があります。これを次の章で学びましょう。
前頁:第24章 学問と科学の定義と目的
ページトップへ:第25章 科学的方法
次頁:第26章 定性的研究と定量的研究