前頁 |▼| 次頁
第31章 教養と学問
長かった講義の最後として、教養と学問の関係をおさらいします。学問の専門分化を前提にしつつも、教養 liberal arts を養成し、自然と人間を総合的に理解することの重要性と、その方法の一端を説明します。
| 目次 |
| 1 専門の概観 2 自然の総合的理解 3 人間の総合的理解 4 まとめ テキストのダウンロード[詳細] 通常版 既述版 配布資料 |
| ADs |
1 専門の概観
現代の学問状況は、分野によって細かく専門 disciplines に分かれており、それを身に付けた人が専門家 specialist でした。
同時に、専門を横断して考える、つまり、学際的 interdisciplinary に考えることも重要になっています。
そして、専門分野でもなくとも各分野を総合的に考える基礎能力が教養 liberal arts であり、総合家 generalist です。
では、講義の最後として、総合家 generalist として、身に付けるべき教養 liberal arts を概観しましょう。
まず前回の復習ですが、学問の研究の対象は、世の中のことほぼすべてです。そして、人間を取り囲む世界の種類に応じて、学問の専門も5つの分野に大きく分けられました。
図30.1.世界―人間―学問 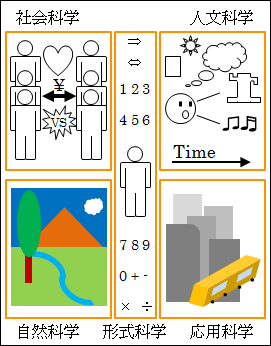
人間存在の根源である自然を研究する専門分野が、自然科学 natural sciences です。
人間存在の基盤である技術や制度等の文明を研究する専門分野が、応用科学 applied sciences です。
人間の存在と関係性である社会を研究する専門分野が、社会科学 social sciences です。
人間存在そのものと精神を表す文化を研究する専門分野が、人文科学あるいは人文学 humanities です。
人間が抽象化した論理と数を研究する専門分野が、形式科学 formal sciences です。
この5つ専門分野 humanities and sciences は、さらに、細かく専門分野に分けることができました。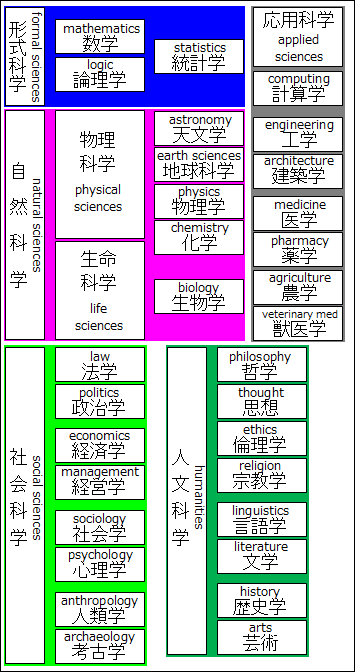
教養 liberal arts を身に付けた教養人あるいは総合家 generalist は、こうした多様な専門分野 disciplines を幅広く自分の頭で考えることができます。
では、各専門分野 disciplines を総合的に考えるためにも、全体として捉えてみましょう。
2 自然の総合的理解
まずは、自然を大きく把握しましょう。
自然と言っても、その対象は、種類も大きさも非常に幅広いです。
普段生活していて、私達に馴染みのあるものは、動物や植物、私達人間の身体といったものがあります。
より大きなものに目を向けると、山脈や大河、海等、そして地球というものがあります。この辺になると、写真とかを使わずに全体像を把握することは難しくなって行きますね。
さらには、地球を飛び出して宇宙になると、大きくなり過ぎて、通常の感覚で捉えることが難しくなってきます。
逆に、より小さいものに目を向けてみると、細菌や細胞といった肉眼では見えない大きさのものもあります。それでも、学校の顕微鏡程度の実験器具でも見ることはできます。
でも、さらに小さいものである分子・原子になると、小さくなり過ぎて、通常の感覚で捉えることが難しくなってきます。
つまり、規模が大きくなっても小さくなっても、私達の感覚でも理性でも捉えるのが難しくなります。
おそらくですが、理科が苦手な人は、規模が大きすぎたり小さすぎたりして、具体的に想起(イメージ)することができなくて、何が何だか分からないということになっているのではないでしょうか。
他にも理科が苦手な理由には、数学が苦手で、自然界を支配している法則を数式で処理できないという場合もあるでしょう。
しかし、数学をそこまで利用しない中学時代に理科嫌いが多く出て来ることを考えると、そもそも想起(イメージ)できないから、というのが大きいかと思います。
でも、自然科学 natural sciences の研究対象は、現実に確かに物質として存在しているものがほとんどです。実は、非常に物質的で観察ができる分かり易い学問なのです。
このことを分かってもらうためにも、自然科学 natural sciences の研究対象を規模の面から総合的に捉えます。1.累乗
そのために、まず仕込みとして、10の累乗という考え方を学びます。
10の累乗は、10の右上に数字を乗せて表記します。10x のように表記して、「10のx乗」と言います。
そして、10xが意味する所は、10をx回掛けるということです。
| 103=10×10×10=1,000 102=10×10=100 101=10 |
10xの乗数xの数だけ、同じ数字10が掛けられているのが分かります。
なお、100は10×0と考えて0とする人がいますが、違います。
100は1と定義されているので注意してください。
| 103=10×10×10=1,000 102=10×10=100 101=10 100=1 |
乗数が0より小さくなって負の数になると、分数・小数になります。
10-1は1/10あるいは0.1となります。
| 103=10×10×10=1,000 102=10×10=100 101=10 100=1 10-1=1/10(=0.1) 10-2=(1/10)×(1/10)=1/100(=0.01) 10-3=(1/10)×(1/10)×(1/10)=1/1000(=0.001) |
こうして見ると、10xは、0がx個続くことを表しているのが分かります。
なお、「累乗」という日本語を見ても意味が把握できます。
「累」は「重ねる」という意味です。「乗」は、掛け算のことです。
したがって、「累乗」は、「重ねて掛け合わせる」ことだという意味が、字から想像できます。
英語では、「累乗」のことを powers と言います。
ですから10xは、the xth power of ten となります。102なら、the second power of ten です。先に10の方を言いたい場合は、ten (raised) to the second power とも言えます。
それで、なぜ10xという数え方を採用するかと言えば、ちゃんと理由があります。
それは、宇宙規模の大きさから原子規模の小ささまで表記するとき、10xを使えば、どれだけ規模が違うのかが分かり易くなるからです。
私達が日常使っているような15mや1500kmなどという表記では不便で、宇宙規模や原子規模の大きさの違いが分かり難くなります。
例えば、地球から月までの距離を皆さんは知っていますか?
地球から月までの距離は、約38万(380,000)kmです。
mに直せば、38に0が7つ続きます(380,000,000m)。
数字が大きくて、どれくらいの距離なのかが何だか分かり難いです。
それでは、地球から太陽までの距離はどれくらいですか?
これは、約1億5千万(150,000,000)kmです。
mに直せば15に0が10個続きます(150,000,000,000m)。数字が大きくなり過ぎて、もう何がなんだか分かりません。
また、白血球の大きさを知っていますか?
種類とかでばらつきがありますが、ここでは約7μmとします。
1μm(マイクロメートル)は、1mの前に0が6つ続く単位なので、0.000001mとなります。
よって、7μmは、0.000007mです。
mに直せば、7の後に0が6個続きます。小さ過ぎて分かり難いです。
宇宙規模になっても細胞規模になっても、0が何個もついて桁が増えすぎて、私達の理解を妨げます。
38万と1億5千万を比べたとき、どれくらいの大きさに違いがあるのか理解するのに少し時間を要します。
下手をすると、大きさの違いが具体的に思い浮かばず、理解できないこともあります。
しかし、ここで、0の数を10x とまとめれば、規模がどれだけ違うのかが分かり易くなります。
0の数を10xとまとめているということは、10xの乗数xが桁数となります。
10xはx+1桁になります。
101なら、1+1=2桁になります。確かに、101=10なので2桁になっています。
なお、乗数xが負の場合は、絶対値を取って|x|+1桁になります。
地球と月の距離は、3.8×108mと表せます。8+1=9桁です。
地球と太陽の距離は、1.5×1011mと表せます。11+1=12桁です。
白血球の大きさは、7×10-6mと表せます。6+1=7桁です。
なお、掛けられている数の3.8や1.5が小数点で表記されているのは、10xだけで桁数を表すようにしたいからです。
ですから、地球と月の距離は、38×107ではなく、3.8×108と表しています。
地球と太陽の距離も、15×1010mではなくて、1.5×1011mと表しています。
仮に38×107のままで、7×10-6と比べると、10xを見ただけでは、桁数がどれだけ違うのかが把握できません。
それでは、桁数を表す10xの部分に注目してみましょう。3.8や1.5、7の部分は一旦無視してください。
地球と月の距離は、108。
地球と太陽の距離は、1011。
白血球の大きさは、10-6。
地球と月の距離(108)を基準にすると、地球と太陽の距離(1011)は、地球と月の距離の1,000倍大きいことが分かります。
計算式は、乗数の差が11-8=3ですから、103=1,000倍です。
地球と月の距離が1,000個分で地球と太陽の距離になることが分かります。
地球と月の距離(108)を基準にすると、白血球の大きさ(10-6)は、地球と月の距離の100兆分の1の小ささだと分かります。
計算式は、乗数の差が-6-8=-14ですから、10-14=1/100 000 000 000 000(=0.000 000 000 00001)倍です。
0が14個もあるので、ちょっと分かり難いですかね。とりあえず、白血球を100兆個一列に並べると地球と月の距離になります。
馬鹿デカい規模のもの、アホ程小さい規模のもの、どちらを比べるにしても、10x以外の部分は、些末な違いでしかないことに気付きます。
3.8とか1.5とか7とかの数は、0が何十個と続く桁の中では、消し飛んでしまうほどの小さな違いでしかないということです。
ちょっと桁数がデカすぎて想起(イメージ)し難かったかもしれませんね。日常生活に照らして言ってみましょう。
身長180cmと160cmの20cmの違いは、人間として見たとき、大きな違いに感じられます。180cmの人のと160cmの人から受ける威圧感は全然違いますしね。
でも、富士山つまり3000m級の山と比べるとき、身長180cmと160cmの違いなんて無いに等しいものとして扱いますよね。
人間大の大きさだけではありません。3階建の建物か2階建の建物であろうとも、富士山の前では、あまり違いがありません。
このように、10x という形で表すとき、桁数が大きくなると、3.8×108の3.8とか、1.5×1011の1.5とかの数字は小さな違いであり、108や1011の桁数を表す部分が中心になるのが理解できます。
もちろん、実際に、各専門分野で研究するときは、そのような些細な違いが大切になることも多いですが、今は、教養として自然を大きく捉えようとしているので、気にしないでください。
2.自然の大きさ
以上のように、10xという捉え方で、自然科学 natural sciences を規模の大きさから見て行きます。なお、今から見せる絵は、Charles Eames Jr の映画 powers of ten
また、専門と科学の分類は、物理学界の超有名学者 Feynman 氏の The Feynman Lectures on Physics
さて、まずは私達人間に最も馴染みのある規模である100(=1)mの世界です。

この人は某大学の建物の前の芝生で寝ています。本も転がっていますね。
この100(=1)mの世界で、私達の日常生活は営まれています。食べたり寝たりも、この100(=1)mで行われています。
範囲を10倍してみましょう。101(=10)mの世界です。

人の全身が見えます。本は、少し小さくなり過ぎて判断し難くなっています。
101(=10)mは、100(=1)mの世界に比べて、かなり大きな世界になりますが、まだ日常に馴染みのあるものです。
ここには建物は見えてませんが、家などもこの101(=10)mの世界に収まります。学校にある体育館などもこの規模に収まりまることがほとんどでしょう。大きな動物や植物もこの世界に収まります。クジラもこの辺の大きさに属しますね。
ちょっと歩けばすぐに移動できるような規模です。
さらに10倍して範囲を広げた102(=100)mの世界に行きましょう。
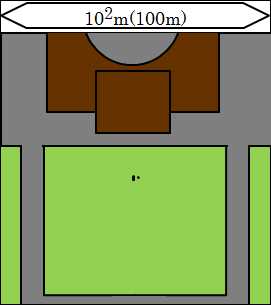
人が点のように見えます。と言うか、「これは人です」と言われないと、分からないようになってしまいました。小さな講堂やビルなら全体が見えるような大きさです。102(=100)mは、101(=10)mのよりもずいぶん大きな世界です。
それでも、まだ日常生活に馴染みがあります。
講堂や学校は日頃から使っていますからね。他にも、ジャンボジェット機や新幹線・電車などもこの辺の大きさになります。陸上競技である100m走もまだ直線で行われています。全力で走れば10秒前後で移動できます。しかし、200mとか400mとかになってくると、話は変わってくる程度の大きさです。
自然も山や川の大きさの規模になってきます。
森ではなく山と認識できるようになります。湖ではなく川だというのが分かるようになります。
このように、102(=100)mは、人間は見えなくなりますが、人間がつくった建物などは見えるので、技術と文明の世界に焦点が当たってきます。
さらに10倍して範囲を広げた103(=1km)の世界に行きましょう。
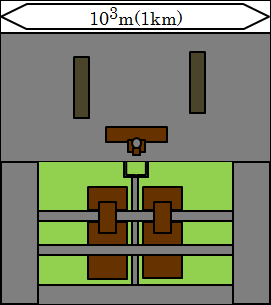
人間は、もう気配すら感じられなくなり、まったく見えません。建物は見えますね。103mは、1000mなので1kmとなります。
103(=1000m=1km)の世界は、人間の技術と文明の世界がよく分かるものになります。これは、お城や超高層ビルの全体も余裕で見える程度の規模です。なお、1kmは鍛えた人なら3分程度で走ることができます。一般人でも5分程度くらいで走れます。
ここには映っていませんが、山が収まる程度の規模になってきます。富士山は3,766mですね。
さらに10倍して範囲を広げた104(=10km)の世界に行きましょう。
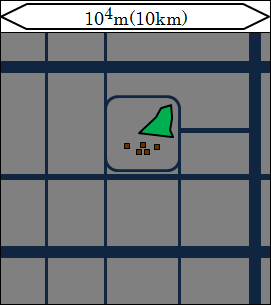
街が形成されているのが見えてきます。かなり大きい建物なら、人間がつくった建物だとまだ認識できます。しかし、小さな建物なら個々の建物の存在が希薄になってきます。
短い川なら、104(=10km)の規模におさまるものも増えてきます。山は山脈としても認識できるようになります。
ちなみにイギリスとフランスの間にあるドーバー海峡は約34kmです。対馬と朝鮮半島の海峡は約50kmです。短い海峡なら、この104(=10km)の規模に収まることが分かります。
運動選手が104(=10万m=10km)を走ったら、30分未満程度になります。
さらに10倍して範囲を広げた105(=100km)の世界に行きましょう。
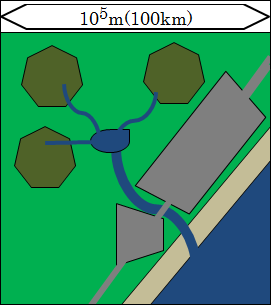
105(=100km)の世界では、街全体の姿が見えます。もう個々の建物が消えてしまいます。1つ1つの建物が、どのような形をしているのかということは分からなくなります。でも、まだ人間がつくった建物が存在しているのは何となく分かり、文明が確認できます。
山や川の全体像がいくつか見えてきます。日本一長い川である信濃川が約367kmです。日本最長の奥羽山脈は約500kmです。
鍛えた人間なら、105(=100km)を12時間くらいで走れるでしょうか。毎年夏にある某テレビの特別番組では24時間かけているので、それくらいかかるのかもしれません。基本的には、車や電車で移動する距離になりますね。車や電車なら2時間前後かかる距離になってきます。
さらに10倍して範囲を広げた106(=1000km)の世界に行きましょう。
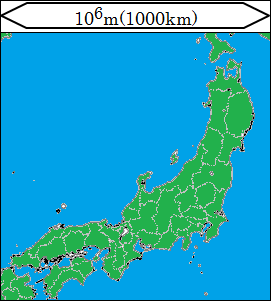
本州が見えています。この図では分かりませんが、目を凝らして、人間がつくったものはないかと探せば、何か発見できるかもしれません。しかし、もうほとんど人間の生きている形跡は見えてこなくなってしまいます。
その代りに浮き上がってくるのが、島や海、山脈や湖・河川などといった地球の構造です。
こうしたものが複数同時に確認できるようになり、地質学的な構造がハッキリと見え始めます。
東京から福岡に移動すれば、1000km以上の移動になります。
ヨーロッパで流れるライン川が約1233kmです。アルプス山脈が約1200kmです。
南米のブラジルを流れる世界最長の川であるアマゾン川が約7025kmです。南米の世界最長のアンデス山脈が約7500kmです。
このように、106(=1000km)は地質学的な構造が見えてきます。
さらに10倍して範囲を広げた107(=1万km)の世界に行きましょう。

地球のほぼ全体が見えます。夜に都市の灯りで照らされている場合を除けば、人間の文明は、もう肉眼では確認できません。
つまり、ほぼ完全に人間の規模ではなくなってしまいます。
ちなみに、地球の直径は、12,700kmですから、1.27×107mと表せます。
このように、107は地球全体の規模、そして宇宙の世界になってき行きます。
この辺の大きさになると、もうひたすらデカいとしか感じずに、具体的に思い浮かばなくなり始める人が増えてきます。
次は、102(=100)倍して範囲を広げた109(=100万km)の世界に行きましょう。

地球は点のように見え、広大な宇宙という背景に埋もれて行きます。
黄色の楕円は月の軌道になります。
そして、地球と月の距離は、38万(380,000)kmでしたから、3.8×108mと表せました。
月が地球を1周する軌道がまるまる収まっても余裕がある大きさです。
109(=100万km)という規模は、ちょっと普通の感覚では、捉えられないですね。
さっきの地球全体と言われれば、地球に住んでいる分、「大きいなぁ」と感じられたかもしれません。しかし、月は、夜に遠くの空に見えるだけです。その月が、地球を1周するのよりも大きいと言われても、何だか分かり難いです。
さらに10倍して範囲を広げた1010(=1000万km)の世界に行きましょう。
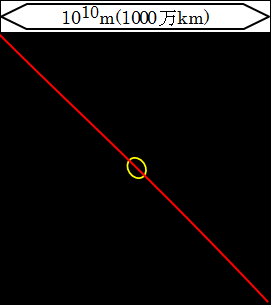
もう地球は小さすぎて見えませんね。地球の周りを回る月の軌道も小さな楕円にしか見えません。
図の赤色は、地球が太陽の周りを回る軌道、つまり、公転軌道の一部です。
1010(=1000万km)の世界は、もう十分に大き過ぎて、私達の通常の感覚で理解するのが、ますます難しくなってきます。
ここで、ちょっと思い出してほしいのですが、地球から太陽の距離は、約1億5千万(150,000,000)kmなので、1.5×1011mでした。
したがって、地球と太陽の距離は、1010m(=1000万km)よりも、もう1桁多い1011m(=1億km)です。
そうすると、図の赤線部分において、地球が赤線の端から端まで移動しても、私達はたったの4日分しか過ごしたことになりません。
1010m(=1000万km)とは、地球の移動距離にしたら、たったの僅か4日分。想像しにくい規模の数字になってますが、宇宙の大きさの凄まじさは分かって来ます。
次は、ちょっと多めに倍率を上げて、103(=1,000)倍して範囲を広げた1013(=100億km)の世界に行きましょう。
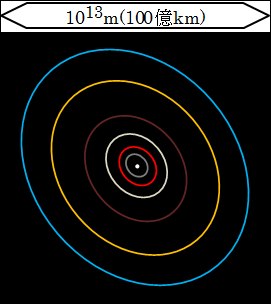
太陽系全体がスッポリと入る大きさになっています。
太陽は、図の中心で宇宙の中に白く光る点にしか見えません。もう10倍して1014(=1000億km)の世界に行くと、完全に点になって太陽だって分からなくなります。
図の青色の楕円は、海王星の公転軌道です。黄色は、天王星の公転軌道です。茶色は土星の公転軌道、薄い灰色は木星の公転軌道、赤色は火星の公転軌道、濃い灰色は地球の公転軌道です。金星と水星の公転軌道は、地球よりも小さいのでゴチャゴチャし過ぎになるので図に描きこんでいません。
このように、1013(=100億km)の世界では、太陽の周りを公転する惑星すべてを目にすることができるわけです。
いやはや、とてつもない限りです。現在のところ、人類が人工衛星を送り込めている範囲でもあります。
まだまだ行きましょう。また、103(=1,000)倍して範囲を広げた1016(=10兆km)の世界です。

1016(=10兆km)の大きさになると、ついに光年という単位が出てきます。
1光年は、1年に光が進む距離を意味します。
2光年なら、光が1年に進む距離の2つ分になります。
たまに、光年を時間の長さと勘違いしている人がいますが、違うので気を付けてください。光年は、kmやmと一緒で距離の単位です。
1光年=9.5兆m=9.5×1015mなので、ほぼ10兆km(=1016m)となります。
光の速度は、約3億m/sです。1秒に3億m(=3万km)進むってのもちょっと理解し難いですね。
でも、その光の速さで1年進むと約10兆kmとなります。これが1光年です。
いやはや果てしないです。この1光年という単位が普通に使われるくらい、宇宙は大きいのです。
講義の時間の関係のため倍率を一気に上げます。また、105(=100,000=10万)倍して範囲を広げた1021(=10万光年)の世界に行きましょう。

渦巻銀河が見えます。
中心で光っているのが、銀河の中心部分です。ここに太陽のような自ら光を放つ恒星がいっぱい集まっています。そこを中心にガスが渦巻いてます。
これが私達の住む地球が属する太陽系が属する銀河である天の川銀河になります。
この図は、銀河の外から銀河を見ていることになります。逆に、この銀河を私達の住んでいる地球から見ると、天の川として観測することができます。
銀河は、私達のいる天の川銀河だけでなく他にもたくさんあって、宇宙に散らばって移動しています。
40~50億年後には、最大のアンドロメダ銀河と衝突すると予測されています。でも、安心してください。ガスが取り巻いているといったように、銀河内はスカスカなので、銀河同士がぶつかっても、だいたいはすり抜けるはずだと予測されています。
102(=100)倍して範囲を広げた1023(=1000万光年)の世界に行きましょう。

あれだけ大きく見えた銀河も102(=100)倍すると、点が光っているようにしか見えません。銀河が複数あるのが分かります。
銀河が50個程度集まったものを銀河群と呼ばれます。
それ以上の数になると銀河団と呼ばれるようになります。
銀河群や銀河団は、銀河同士が重力によって互いに引き合いながらまとまって移動している集まりです。
太陽系では、太陽に引っ張られて移動する惑星の集まりを太陽系とまとめたように、銀河も銀河同士で引っ張り合いながら、ある種の集まりのようになっています。
さらに、10倍して1024(=1億光年)の世界になると、超銀河団となります。
銀河団同士が集まったもので、宇宙最大の結合物です。
そして、1026(=100億光年)の世界になると、現在私達が観測できる最大の距離にして大きさなります。
もう少し細かく言うと約130億光年が観測可能な宇宙になります。これは半径なので、直径にすると、約260億光年分の宇宙が観測できることになります。
どうでしょうか。自然科学が対象とする規模の大きさが想像できたでしょうか。
それでは続いて微小な世界の方について見て行きます。もう一度100(=1)mの世界に戻りましょう。

人間の大きさになるとなんだか安心します。ここから次は10-1(=1/10=0.1)倍していきます。
範囲を1/10倍してみましょう。10-1(=10cm)の世界です。

寝ていた人の肌ですね。あとは、今君達が勉強してノートに色々書いていますが、これも、10-1(=10cm)の世界での出来事ですね。リンゴとかが、この規模の大きさになります。日常に馴染みのある大きさです。
さらに範囲を1/10倍してみましょう。10-2(=1cm)の世界です。

肌のしわが鮮明になります。こうやって肌にしわが入ることで伸びたり縮んだりと柔軟性があるわけです。
しかし、いきなりこれを見せられると、人間だとは、分からないかもしれません。
人間という性質が希薄化しています。
また、消しゴムなどが5cm程度の大きさになります。まだ日常に馴染みのある大きさだち言えそうです。
さらに範囲を1/10倍してみましょう。10-3(=1mm)の世界です。
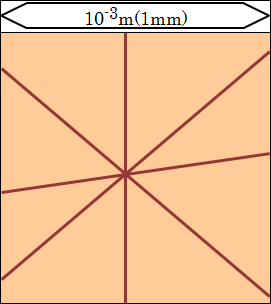
先程の肌のしわに焦点が当たっています。こうなるともう人間だとは分かりません。
10-3(=1mm)の世界は、1粒の砂、つまり、砂粒程度の大きさになってきます。私達の日常に馴染みのある大きさからは、ちょっと離れて来ているのが分かります。
さらに範囲を1/10倍してみましょう。10-4(=0.1mm)の世界です。
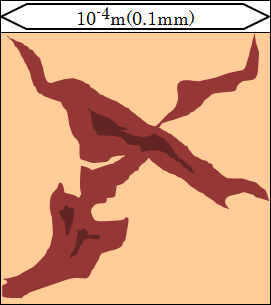
肌のしわが細胞によって構成されているのが見えてきます。個々の細胞が確認できる大きさです。
微生物で言えば、アメーバ等がこの大きさにあたります。
10-4(=0.1mm)の世界は、もう肉眼では観察することが、ほとんどできないはずです。日常の感覚からも、かけ離れた大きさになっています。ただ、学校の授業で顕微鏡などを使ったことがあるはずなので、まだ具体的な印象(イメージ)を持つことができるかもしれません。
さらに範囲を1/10倍してみましょう。10-5(=0.01mm)の世界です。
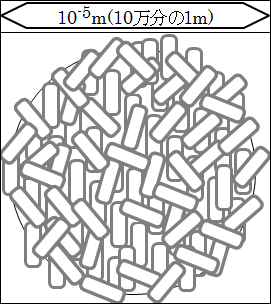
10-5(=0.01mm)、つまり、10万分の1mの世界になると、1つの細胞の大きさになります。
図は1個の白血球です。細胞を観察するのに適した規模だと分かります。
10-5(=0.01mm)の世界は、日常の生活では使うことがまずないような小ささで、理解するのが難しくなってきます。
さらに範囲を1/10倍してみましょう。10-6(=0.001mm)の世界です。
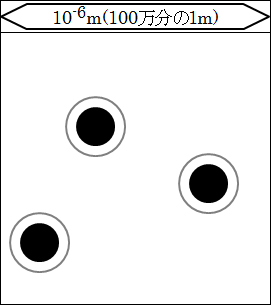
10-6(=0.001mm)、つまり、100万分の1mの世界になると、新しい単位μが使われるようになります。
1μ=10-6を意味します。
そして、1個の細胞の表面を覆っている細胞膜を突き抜けて、中心部分である細胞核が見えるようになります。この細胞核には遺伝子情報DNAが入っています。
また、細菌などもこの大きさになります。
小さすぎて、理解が非常に難しいです。でも、まだ存在していると言われれば、何となくそうなのかなと納得できる範囲かもしれません。
さらに範囲を1/10倍してみましょう。10-7(=0.1μm)の世界です。

10-7(=0.1μm)、つまり、1000万分の1mの世界です。
DNAの二重螺旋構造が見えるようになります。
このDNAが集まって染色体となります。
そして、DNAは、私達の身体的特徴を決定する情報です。こんな小さなものによって髪や肌、目の色、二重であるとか鼻が低いとかが決まっているのです。
また、ウィルスもこの大きさになります。
10-7(=0.1μm)の世界は、あまりにも微小な世界になっていますが、頑張って付いて来てください。
さらに倍率を下げて、範囲を10-2(1/100)倍してみましょう。10-9(=0.001μm)の世界です。

10-9(=0.001μm)は、10億分の1mであり、1000万分の1mmの世界になります。
ここで、新しい単位nが使われるようになります。
1n=10-9を意味します。
ですから、1nm=10-9=0.001μm(=10-6×10-3)=0.000 000 1mm(=10-7×10-2)=0.000 000 001m(=10-9×100)となります。
個々の分子が見えてきます。
分子は原子が結合することで形成されているので、そういう意味では、原子も見えているということにもなりそうですが、主に分子が見えています。
ナノの世界は小さ過ぎて、もう具体的には想像できないかと思いますが、分子が観察できる世界です。
さらに範囲を1/10倍してみましょう。10-10(=0.1nm)の世界です。

100億分の1mの世界では、原子が見えます。
原子が見えると言っても、原子の中は、空っぽに近くスカスカなので、原子に接触しようとしても簡単ではありません。中心部分にまで行かないと何もありません。
図では、原子の中心部分が濃い灰色になっています。その周りの薄い灰色全体で原子となります。
こうなると、10-10(=0.1nm)の世界は、説明されただけでは、「そうなっているのですね」としか言いようがありません。
宇宙が果てしなく大きくて想像し難かったのとは逆に、小さ過ぎて想像し難くなっています。
さらに倍率を下げて、範囲を10-3(1/1000)倍してみましょう。10-13(=0.0001nm)の世界です。

10兆分の1mの世界では、原子の中心部分である原子核が見えます。
この原子核の周りを電子が飛び回っています。ただし、電子は小さ過ぎて10兆分の1mでも見えません。
10-13(=0.0001nm)の世界は、このように、もうがっつり観察するのが難しくなってきます。ですから、話を聴いても、理論上、そうなっているくらいにしか感じられなくなります。
さらに範囲を1/10倍してみましょう。10-14(=0.00001nm)の世界です。
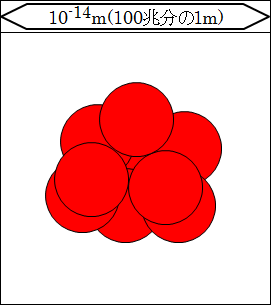
100兆分の1mになると、原子核を構成している陽子と中性子が見えてきます。
陽子と中性子の数によって、原子がどのような性質を持つかが決まります。
この陽子と中性子の組み合わせで、水素やヘリウムといった原子ができあがります。
私達人間の大きさ100=1mを基準に考えると、太陽系全体が1013mだったので、10-14=100兆分の1mは、太陽系全体よりも大きいものを考えるのと同程度に小さいものについて考えていることになります。それだけ私達の日常の感覚から離れたものになっています。
さらに範囲を1/10倍してみましょう。10-15(=0.000 001nm)の世界です。

1000兆分の1mの世界では、原子核を構成していた陽子や中性子の1つ1つが見えます。
つまり、個々の陽子が見えてきます。
そして、陽子が更に小さい物で構成されているのが分かります。その物質の最小単位を素粒子と言います。
素粒子は、クォークとレプトンという2種類あることが分かっています。
複数のクォークによって中性子と陽子が形成されます。
レプトンは電子とニュートリノになります。
こうして、要素還元主義で、どんどん小さく具体的で基礎的な要素に分解して行くと、1000兆分の1mの世界にまで戻すことができるのです。
そして、この素粒子によって原子をつくり出し、その原子の配列を変えれば、すべての物質を作り出すことできます。まぁ、これは理論上の話で、その理論を実践する技術は、開発中で現在まだ存在していません。
ただし、10-15=1000兆分の1mの世界でも十分に0に近いと言えそうですが、素粒子の大きさは限りなく0に近いものと考えられており、どれだけ小さいかは具体的には未だ不明ですが、10-31という考えがあります。
以上、駆け足気味でしたが、私達人間の大きさ100=1mを始点として、宇宙へ向けての大きい方向1026mと素粒子に向けて小さい方向10-15mの両方面を見て行きました。
図31.1.自然界の規模 画像クリックで拡大

10の累乗によって考えることで、大きさの違いが把握できたでしょうか。
乗数が大きくなるにしろ小さくなるにしろ、どこかの値を境に、とにかく大きい、とにかく小さいとしか感じなくなった人も多いかと思います。
最初の内は、それで構いません。
今見てきた規模の違いを頭に入れておけば、理論上のお遊び・空想をしているのではなく、確かに存在する物質を考察しているということが分かるはずです。そうすれば、理科に対して拒絶反応が出ることなく、色々と考えることができるようになるかと思います。
また、学問が専門分野 disciplines に分かれているとしても、科学の分野が切れ目なく繋がっていることも理解できます。
この世のすべての物質は、素粒子によって構築されています。
素粒子によって陽子・中性子が形成されます。
陽子・中性子等によって原子が形成されます。
原子によって分子が形成されます。
分子によって DNA が形成されます。
DNA と分子によって細胞が形成されます。
細胞によって人間や動植物が形成されます。
動植物によって生態環境が出来上がります。
また、分子は生物だけではなく、鉱物なども形成します。
こうして、動植物や鉱物などによって、地球の自然環境ができあがっています。
その地球も宇宙の中で太陽の影響を受けて存在しています。
その太陽も銀河の中の1つでしかありません。
その銀河も銀河団の集まりでしかありません。
最小単位の素粒子から最大の銀河団まで切れ目なく繋がっています。専門 disciplines はの繋がりに切れ目を入れて、分割したものであるのが分かります。
また、こうした素粒子から様々なものが形成されていく過程には、運動法則によって決定されます。
風や海の流れもそうした運動法則の延長線上にあります。
そして、この物理学に代表される自然科学は、数学によって支えられています。
実際、物理学では、数と論理の抽象的な世界の数学の理論によって予測されてきたものが、実在することを観測して発展する場合が何回もありました。
このように、数学は、物質や事象が現実に存在しているのではないかという予想を提供してくれます。それを手掛かりにして、実験をすることで新たな事実が発見できる可能性があります。数学は、世の中の現象の法則を数式化して予測可能にするだけではないのです。
このように、現実に存在する物質は、私達の抽象的思考からも繋がっており、すべては切れ目なく繋がっているのが確認できます。
そして、皆さんの中でも、次のような言説を耳にしたことがある人がいるかと思います。
高校の各教科を大学で専門的に勉強しようとすると、研究分野がより基礎的なものになるという言説です。
| 生物→化学→物理→数学→哲学 |
生物を勉強するなら、化学を勉強することになる。
化学を勉強するなら、物理を勉強することになる。
物理を勉強するなら、数学を勉強することになる。
数学を勉強するなら、哲学を勉強することになる。
こうした言説をそのまま真に受けるのはいかがなものかと思いますが、それでも、一面の真理をついてはいます。
先に見た自然界の大きさと学問の専門分野の関係を考えると、各分野をよく知るには、その専門分野を構成している基礎的なもの、もう1段階下の大きさのものを、よく知っておく必要があるというごく普通の考えに基づいているからです。
そうすると、理科系の人の多くが理科を物理と化学を選択するのも納得がいきます。
物理と化学をやっておけば、上にずれて生物を研究することになっても化学をやっているので助かります。
また、下にずれて数学よりになっても、物理学をやっているので助かります。
結構、物理と化学という2科目の選択は、応用範囲が広い理科の選択になっているわけです。もちろん、本当は理科4科目すべてをやるべきなのでしょうが、時間的にも厳しいから2科目に絞るのも仕方ないという留保つきですが。
さて、今、微小な世界から積み上げて巨大な世界へと繋げ、逆に、巨大な世界を分割して微小な世界へと繋げました。
しかし、微小な世界からいきなり巨大な世界へとも繋がるのが、自然科学の不思議なところであり、面白いところでもあります。
まず、観測可能な宇宙の世界は、私達の通常の感覚では捉えることが難しい程の1026mという広大さです。
しかし、その広大な宇宙の起源を知るために、超微小であり物質の最小構成単位である素粒子の世界10-15mを調べているのです。
と言うのも、素粒子は、宇宙を構成する最小単位であると同時に、宇宙の誕生と関わっているからです。
宇宙中に散らばって漂っている素粒子を観測することで、宇宙の歴史が分かります。
宇宙の始まりは、ビックバンと言われています。
今現在宇宙に散在している物質のすべては、このビックバンの前に1か所に存在しており、ビックバンと同時に拡散して行ったと考えられます。
また、宇宙が始まった頃には、重力、原子や分子を結合させている力や電磁力等、今では別々の力と考えられているすべての力が、1つの力に統一されていたという大統一理論も考えられています。
ビックバンも大統一も理論仮説であり実証できていませんが、こうしたことが、10-15の世界を通じて、1026の世界を解明できるわけです。
これは10-15の世界から直接的に1026の世界を見ていることになります。素粒子を観測しているだけで、原子や分子、細胞と積み上げていません。
そうすると、図31.1.自然界の規模では、10-15から1026までの世界は1直線上に並べられていますが、これは円状で理解する方が適切だと言えます。
図31.2.自然科学の循環 画像クリックで拡大
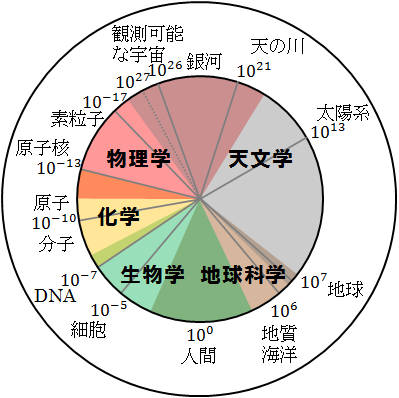
こう見ると、ますます専門分野の境界とか分類が、あまり意味をなさないことが分かります。
一直線上に専門分野を分類する図(31.1)で考えると、宇宙を対象とする天文学から下に行けば行くほど、素粒子から積み上げていく物理学に還元できることが分かります。
物事の始まりが物理学で、それから積み上げたら宇宙になるという印象が得られます。これは自然科学の対象の多様性を知るのに便利です。
図31.1.自然界の規模

こう見ると、教養 liberal arts が、専門 disciplines を修めるための基礎的な能力であるとしたら、「物理学を身に付ければいいのか!」と思いがちです。
しかし、そんな単純に物事は分けられないことが、円形並べると分かります。
対象の大きさを円形に並べると、専門分野のどこから始めても、一周回って元に戻って来ます。
自然科学が全体として繋がっており、専門分野に分けられていても、「ここからここまで」とはならないことが分かります。
図31.2.自然科学の循環
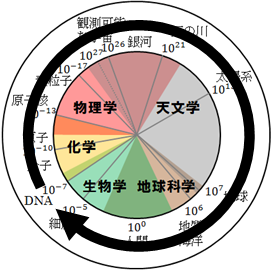
最も基礎的な物質を研究する物理学だけではなく、自然を総合的に把握することの重要性が分かります。したがって、こうした自然を総合的に理解するのが、教養 liberal arts の第一歩になります。
そして、専門 disciplines は、全体が繋がっているものの一部分だけ便宜的に切り抜いているだけにしか過ぎないことを理解しておかないといけません。
これを踏まえて、改めて円形に並べられた対象と専門分野の対応を整理しておきます。
まず、自然科学は物理科学と生命科学と分けることができました。
物理科学は、天文学・地球科学・物理学・化学でした。
生命科学は、生物学でした。
もちろん、この分け方は、現代の学問が学際的になっているので、強固なものではなく、分野横断的なものも重要になっています。
自然科学の背景には、数学や論理学である形式科学があります。この形式科学によって、自然科学は統一的・体系的なものにできます。
図31.3.自然の総合的な理解 画像クリックで拡大

そして、自然科学の知を利用して、技術を開発し文明を築く応用科学へと繋がって行きます。
ちなみに、学問が科学として専門分化する前の、哲学・自然哲学・博物学(自然史学)のときには、以下のような大まかな分け方をされていました。
図31.4.学問未分化時の関係 画像クリックで拡大
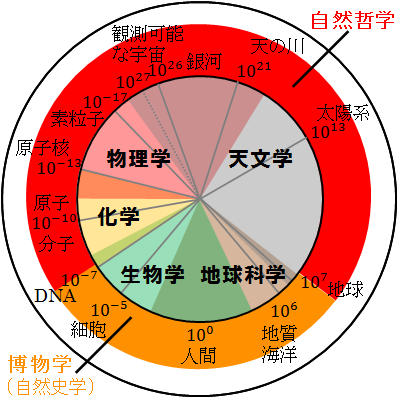
以上が、教養 liberal arts として、自然を総合的に捉える試みの第一歩でした。
こうした自然に囲まれて、私達人間は文明を築き生活をしています。
それでは、次に、自然に制約を受けながらも生活している人間について総合的に見ます。
自然科学の知で言えば、10-2(=1cm)から106(=1000km)が中心になります。
図31.5.自然と人間の関係
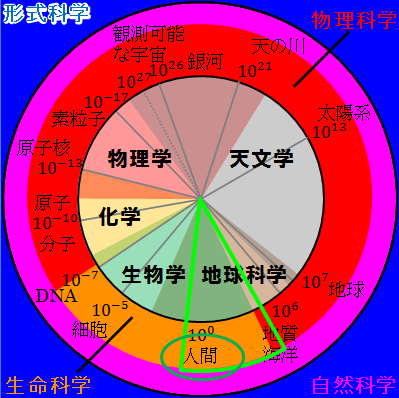
生物学の一部と地球科学の一部が、人間を制約する中心です。
ただし、生物学と地球科学は物理学・化学・天文学と相互に関連していることは言うまでもありません。
また、現代のグローバル化(国際化・地球規模化)した世の中では、107(=1万km)まで広がっていますし、宇宙開発も考えれば、それ以上になります。
そして、自然科学に基づく応用科学による技術と文明の発展は、人間の在り方や生活に多大な影響を与えていることも覚えておいてください。
3 人間の総合的理解
次は、自然の中に生きる人間について、総合的に考えましょう。
日本に住んでいると、文明の発展がすざまじく、いわゆる森の中・山の中といった、人間の手が余り入っていないという意味での「純粋な自然」の中で生きるということを経験しなくなりました。
しかし、人間の祖先はサルと近く、自然の中で生きていました。
そして、サルから進化したのが今の私達である人間です。
二足歩行すれば人間なのか、道具を使えば人間なのか、言語を操れば人間なのか、「人間」という言葉1つとっても色々な考え方があります。が、ここでは細かいことは抜きにして、とりあえず現代の我々の原型となったものが、人間としておきましょう。
とりあえず、最初の人類はアフリカで発生します。
そして、アフリカから全世界に移動をして、各地域の自然環境に適応して、黒人や白人、黄色人種などに枝分かれして行きます。
さて、原始的な人間は、独りではなく、群れをなして狩猟採集生活をしていました。
石を打ち砕いて鋭利にした石器は、狩りを行うのを楽にしました。また、火を使うことで、食糧の加工の仕方が大幅に広がり、食べられる物が飛躍的に増えます。さらに火は、寒さにも耐えられるようになります。
このように、道具を使うことは、現代の文明を支えている技術の始まりと考えることができます。
道具は、人間にとって都合の良いように自然環境を変形させることが可能になります。道具や技術を使うことで、人間は生存確率を飛躍的に上げることができます。
人間は、単なる鳴き声だけではなく、言葉を話すことで複雑な意思疎通(コミュニケーション)ができるようになります。
喜怒哀楽は涙を流す、目を吊り上げる、叫ぶ、うつむく、笑うなど身体で表すことができます。しかし、言葉を使えばそうした感情をもっと詳しく説明できます。さらに、言葉は、狩りに必要な緻密な作戦なども立てられるようになります。
また、言葉は人間の文化や考え方などを保存して後世に伝えられるようになります。
言葉を使うことで、色々な事象を定義して、知識として伝えられる量が爆発的に増えます。言語の使用によって、人間は複雑な思考ができるようになりました。
言葉によって、様々な事柄を考えることができるようになると、人間は色々なことを「何故だろう?」と疑問を持つようになります。
哲学の始まりです。色々と考えて、自分なりに答えを見つけ出して説明しようとします。
そうした考えが蓄積されると、思想が形成されます。色々な考え方をまとめるようになります。
また、知識や思想がたまってくると、人一人では記憶できなくなります。また、記憶は容易に忘れ去られてしまいます。そこで、文字に残して文章として伝えられるようになります。
文字の発明です。
現代では、文章は物語の他に論文や説明文も多いですが、最初期は、物語が多かったかと思われます。
自分の思想や考えかたを伝えるとき、物語形式で述べる方が伝わりやすいからだったと考えられます。文字が発明される前は、すべて口頭伝承だったので、単なる説明は抽象的になりやすく、中々覚えにくいものです。
そこで、物語形式ならば、具体的な出来事と結びつけるので想像しやすく、言いたいことを伝わりやすかったと考えられています。小さな子供に物事や道徳を教えるときに、昔話や説話を読み聞かせるのと同じです。ですから、文字が発明され、文章が残され始めたとき、物語形式が多かったのだろうと予想されます。
文学の誕生です。
こうして、文字に残されることで、言葉で知識を伝達できる量がさらに飛躍的に増大します。また、記録として残ることになるので、人間の歴史がより詳細に分かって来るようになります。
また、哲学や思想が発達すると、それを言葉以外にも表現しようとするのも、人間の性です。
芸術の誕生です。
美術や彫刻、音楽などで色々な考えを表現します。こうして人間は単に食って寝て殖えるだけではなく、人間らしさ・自然との関係性を捉える精神性の発露たる文化を発達させるようになっていきます。
こうした思想や文学や芸術といった精神と文化は宗教としても現れます。
宗教は、神や霊的な存在を用いて、未知の事柄に説明を与えてくれます。
こうして、人間は分からないという不安から解放されます。
また、そうした宗教は、文化的な結実でもありますから、人間の生活と社会を規律します。
これは道徳や倫理と深い関係を持ちます。
何が正しいことで、何をやってはいけないのか、といったことを精神的な面から規律します。そのため、同じ宗教を信じる人同士では、共通の見解ができ、意見の対立が少なくなるので、共同生活が容易になります。
さて、宗教や文化が共通している人は共同生活がしやすいと述べましたが、これは人間がある程度の人数が固まって集団で生活していることを意味します。
狩猟採集生活のときも、もちろん、そうでしたが、農業を始めると余計に集団での生活が大切になってきます。つまり、人間は社会を形成していることになります。
したがって、社会は、文化と文明を基礎として出来上がっています。
そして、社会の中で、人間関係を構築しながら、色々な活動が行われます。
人間は、社会の中で様々な感情を抱き、考えを持ちます。色んな人と出会い、出来事に触れることで、共感したり対立します。物事をどう捉えるかも多様です。このように、人間は、社会の中・人間関係の中で、様々な心理状態となります。こうして、私達は社会の中で生きていくことになります。
また、社会の中では、個々の人間は役割分担をしています。
ある人は農業に従事して食糧を生産したり、工業に従事して衣服や住居をつくったり、商業に従事して物流を円滑化させたりと、各人は様々な役割を担っています。
個人個人が、社会の中で役割分担をしていれば、余分に持っている物もあれば、足りない物もあります。ですから、余分な物を不足している物と交換します。
これが経済活動です。
原始的な状態では、物と物同士の交換である物々交換でしたが、現代では、お金を媒介させて物を交換するようになっています。
また、社会で生活していると、色々な意見の対立が生じます。
同じ利益を共有している人同士が結びついて、利益集団を形成します。そして、対立する利益集団と争います。
これが政治です。
こうして互いに争いながら色々な約束事を決めて行きます。ある時は、特定の利益集団の意見が大幅に採用され、またある時は、社会全体の公平性を上げるような取り決めができたりします。
意見対立や調整は、口約束だけでは、「言った、言っていない」の争いになりかねません。争いが再度誘発されかねません。
そこで、取り決められた約束を法律として文字に起こして文章で残します。
これで口約束だけではなく、物的証拠として約束事が残るので、口約束による争いはなくなります。
また、法律があることで、何をやって良いのか、ダメなのかが明確になりますので、社会生活が送りやすくもなります。そして、何か意見対立が起きても、既に制定されている法律に基づいて処理すれば、後だしジャンケンではないので、公平です。もし法律がなければ、「これやったら後で罰則を受けるのではないか」と思うと委縮してしまいますが、法律が存在していれば、そういったことがなくなります。
ただし、法律に規定されていないなら、何をやっても良いということを推奨しているわけではありませんからね。
経済にしろ政治にしろ、一人で何かするわけではありません。社会の中で、人間はさらに小さな集団をつくって活動をすることが多いです。利益集団も集団の一例です。
集団の中で人間がバラバラに動くと、収拾がつかなくなります。そこで、組織を整備して命令系統を明確にして管理するようになります。
何かを行うときには先導者や統率者を頂点として集団が形成されるのが普通です。もちろん、皆が平等であり対等だという理念もありますが、数人程度ならそういった平等意識の徹底も可能でしょう。が、多数の人で活動するときにそんなことをしたら、十中八九は上手く行かずに崩壊します。
組織化と管理は避けては通れません。
こうして、社会の中に、複数の集団が形成され、それをまとめるように、国家が形成されます。
国家はかなり抽象的な概念になります。
社会と言えば、私達が実際に日常生活を営み、経済活動をしている場なので、ある程度は漠然としていますが身近に感じます。
しかし、国家になると、複数の社会をまとめたものになるので、距離が開きます。
国家が複数の社会をまとめるものであるという点では、自分が所属する社会にも関係するので、国家と関わっています。
他方で、国家が複数の社会をまとめているため、自分が所属しない社会のために動くことを意味します。そうすると、日常生活では自分とは関係のないことや重要ではないこと、自分の利益と相反することを国家が働くこともあります。
したがって、国家が自分とは関係のないものに思えたり、敵対的に見えたりすることが多いです。ですから、広い視野で全体で見て、国家とは何なのかということを考える必要があります。
そして、世界中で国家が形成されています。
複数の国家 nation states が、世界規模で相互に関係し合っています。まさに、国同士が接し合っているので、国際的 international な状況です。
国家は、時には争い、時には協調し、政治や経済を動かし、民族問題や環境問題に取り組んでいます。その最たる例が、国際連合 United Nations になります。
なお、最近はグローバル化(国際化・地球規模化)によって、国家の概念を崩す動きも出ています。「国家の枠に囚われるのは古い。国から飛び出せ」と煽る人もいますからね。
左翼的な言い方をすれば、世界市民主義(コスモポリタニズム)と言えるでしょう。
右翼的な言い方をすれば、新自由主義(ネオリベラリズム)となるでしょうか。
世界市民主議(コスモポリタニズム)は、地球に住む一個人として、国家に囚われることなく協調して結びつこうという考え方です。「人類皆兄弟」の精神です。
だいたい、この精神は、歴史的に見て失敗することの方が多いです。まぁ、難しいでよね。だって日本のことですら、他人に対して無関心だったり、対立する人に対して過度な批判をするのに、国家という規制装置なしに、外国の人とまで上手く行くなんてのが無理難題ってもんです。
それでも、失敗しながらも少しずつ前進しているからいいではないか、と言う人もいますが。
新自由主義(ネオリベラリズム)は、主に経済活動の分野で言うことが多いですが、国家の役割を最小限に留めて、自由な市場経済を目指しています。ほぼ完全な自由市場を世界でつくろうと試みます。民族の共同体を重んじるはずの右翼なのに、新自由主義(ネオリベラリズム)という国家の枠にとらわれない経済活動ってのもなんだか奇妙ですが、それだけ現代の世界と思想は複雑怪奇になっているのでしょう。
この新自由主義の理念は、経済の自由を謳っており、国家の枠組みを残している考えに見えますが、行き着く先では実質的に国家の解体をしています。国家の役割を警察とかの最小限にしていけば、次第に国家が存在する意味がなくなってきます。世界のどこでも同じように活動できるのなら、日本に拘る必要もありませんからね。
左右いずれに振れるのかは分かりませんが、果たして国家なしに個人として存在することが耐えられるのかどうか皆さんも一度色々と考えて見るといいでしょう。教養 liberal arts が「自由人のための技芸」だと強調して説明してきましたが、果たして、自由主義者 liberal が言うような、何にも縛られない完全に独立自尊した個人など本当に存在し得るのか、それで世の中は回り、自分も生存できるのか、考えてみください。
さて、一言に「人間」と言っても、人間の精神や文化に注目したり、人間の活動と関係が織り成す社会に注目したり、どこに注目するかによって、「人間」自体をどう理解するのかも変わって来るのが分かります。人間とは、かくも多様な存在なのです。
図31.6.人間の総合的な理解 画像クリックで拡大 
したがって、学問の専門 disciplines は、人間の精神や活動の一部に注目して研究していることになります。
そういう意味では、人文科学や社会科学が「人間」について研究しているのは間違いありませんが、その専門研究は、「人間」全体ではなく一部であることに注意しておかないといけません。
ですから、文学者、哲学者、思想家、社会学者、政治学者、経済学者、法学者、といった各専門家の発言は、一面的なものでしかないのが分かります。専門分野 disciplines は、「人間」に対する部分的で側面的な理解になります。
自分の頭の中が、ある専門の考えに縛られていると、他分野の専門家の意見が何だか的外れな発言に聞こえたりしやすいです。
例えば、社会的動物の面に注目して社会学的に考えると、経済的動物である経済学の視点が抜け落ちたり、政治に対してやたら攻撃的になる等します。
しかも、「人間」が、同時に様々な活動を行うので、1つ1つの専門分野 disciplines を綺麗に「ここからここまでは、~学」と分類できないことも分かります。
社会的な活動を行うだけで生きている人間なんていません。地域社会で活動すると共に、企業で経済活動をしているものです。どの一側面だけに注目しても、他の側面の要素が流れ込んできます。
図(31.6.人間の総合的な理解)では、便宜的に専門を丸で囲んでいますが、これはあくまで理解しやすいように表しているだけです。
実際には、哲学を中心に、色々な専門が派生しており、専門の境界は曖昧です。
言語、思想や文化は、社会状況や時代によって移り変わるものです。
社会も経済活動に支えられています。
政治的な決定は、国家を通じて社会の隅々にまで行き渡ります。
その国家も、鎖国をしていないので、国家同士の関係なしにはもう考えられません。
専門として、一部を切り抜いても、結局「人間」の精神や活動を研究している限り、他の専門分野を完全に無視して考えることが難しくなってきます。
このように、専門分野 disciplines は、典型的で特徴的な「人間」のある部分に注目しているたけで、各専門の境界線は曖昧になっています。
したがって、必然的に学際的 interdisciplinary な研究になりやすいです。
このことは、具体的な人間一人について、一部を切り抜いて捉えようとしても、その人を全体として理解できないことからも分かるかと思います。
人を評する方法・視点は様々です。
「外見」を評する場合には、「美人」とか「不美人」とか。
「性格」を評する場合には、「優しい人」とか「意地の悪い人」とか。
「頭脳」を評する場合には、「聡明」とか「暗愚」とか。
「身体能力」を評する場合には、「運動神経が良い」とか「運動神経が悪い」とか。
どれも一面的な個人の捉え方です。
例えば、ある人A は、「美人」で「意地が悪い人」で「暗愚」で「運動神経が悪い」人がいたとします。
このとき、その人A についての評価は専門家によって異なります。
「外見」を重視する人にとって、その人A は非常に素晴らしい人だと評価を下すでしょう。何たって「美人」ですからね。
しかし、「性格」を重視する人にとっては、その人A に対する評価は低くなります。「意地が悪い人」は「性格」に難がありますからね。
他にも「頭脳」を重視する人や「身体能力」を重視する人も A に対する評価は低くなります。
このように、どの部分に注目するかによって評価が変わって来ますが、どの部分に注目して捉えても、ある人A 全体を理解したことにならないことが分かります。
「外見」を重視する人は、ある人A の「美しさ」を肯定的に評価しているのだから、それを深めて行こうとすると、どうしても身体の筋肉量と脂肪量の均衡が気になり始めます。そして、それは、「身体能力」への理解が必要なことを意味します。
このように、専門1つとっても、その境界は曖昧になっていきます。
結局、ある人A を理解するには、部分に分解して捉えるのではなく、全体として捉えることが大切だと分かります。
つまり、総合的に考えることが大切であり、だからこそ、教養 liberal arts の重要なのです。
このように、専門 disciplines とは、多様な人間の精神や活動の一部分に焦点を当てて理解しようという試みです。
そして、そうした各専門によって部分的に理解できたものを総合的に考えるのが教養 liberal arts です。
何かの専門 disciplines に長けていても、それは部分だけを知っているだけです。部分以上のことは分かりません。世の中を幅広い視野で捉えて考えるには、教養 liberal arts が重要なのです。
以上のように、こうした多様な存在である「人間」を様々な視点から考えて分析でき、かつ、総合的に考えることが、教養 liberal arts だと理解できました。
教養 liberal arts が、専門 disciplines を修めるための基礎的な能力であるので、1つの専門に囚われることなく、どの専門分野の基礎を身に付けておくことが大切になります。そうではないと、「人間」を総合的に考えることができません。
4 まとめ
以上で、自然科学、形式科学、応用科学、社会科学、人文科学という専門分野 disciplines を総合的に理解するために、専門分野に囚われることなく、自然と人間を俯瞰(全体を眺めることを)しました。
細かく分類された専門 disciplines ではなく、総合的に考えるための基礎的な能力が教養 liberal arts です。
実際に、教養 liberal arts を身に付けることは大変です。
幅広い知識が必要ですし、論理的な思考力が必要となります。
知識は、実際に体験したり、学校の勉強や本を読んだりして仕入れることができます。このとき、自分の興味のある分野の知識を伸ばすことも大切ですが、少々難儀であっても、自分の苦手分野や興味の薄い分野の知識も積極的に学ぶように心掛けることが大切です。
要は、人口に膾炙した言葉、あるいは、耳に胼胝ができる言葉で言えば、「何事にも興味関心を持て」ということです。
そして、その知識を自由に扱うために、必要な論理的な思考の方法と道具は、第 I 部 論理的思考、第 II 部 論理的な問題解決で学びました。この2つの部で、基礎的な論理的思考とそれを実践的に扱うための道具の扱い方を説明しました。
このとき、で専門的な知識を使って結論ありきで説明することを可能な限り避けました。少々長く回りくどくなっても、できるだけ手元の知識を1から積み上げて考えることを重視しました。
これは、教養 liberal arts の練習であり、「自分の頭で考える」過程をじっくりと学んで欲しかったからです。
もちろん、専門分野 disciplines で結論が出ていること、これを当たり前のことと受け入れて既存の知識として使えば、簡単に答えが出せます。
しかし、そういった知識は、諸刃の剣です。知識は素晴らしいものですが、その知識がどのように生み出され、使えるのかということを学ばないと片手落ちどころか害悪になる可能性もあります。
知識に頼ることの害悪の1つが、知識による思考機会の剥奪の可能性です。
知識は、問いに対する答えであるので、非常に便利です。しかし、実は既存の知識を問題に当てはめているだけで、考える機会を奪ってしまうことも多くあります。考える癖がなくなると、「知っていることに対しては答えることができるが、知らないことに対しては何も答えられない」という状況が生じやすいです。
そして、思考機会の剥奪は、知識の濫用の危険も生じさせます。
論理的に考える癖がないと、未知のことに出会ったとき、既存の知識を濫用して、本来は適用できない事柄に対して知識を適用して、答えが導けた気になりやすいです。
何も知らないと、お手上げになって終わりです。が、知っている事柄と似たものに出会うと、観念連合が起きやすいので、ついつい知識を勝手に当てはめてしまいます。それでも、論理的に考えれば、何かおかしいぞと感じ、誤りに気付けます。しかし、考える癖がついていないと、論理的思考ではなく、知識を単に当てはめているだけなので、正しい保証は考えていない場合と変わらないことになります。しかし、知識の正しさに自信を持っている分、当てはめ方に疑問を抱かず、そのまま通してしまう危険が高くなります。
さらに、これは知識への過信にも繋がります。
知識があると、人間色々なことを理解していると思いやすいです。そして、それが自分の判断の正しさに対する自信となりやすいです。ですから、考えることを飛ばして既存の知識に頼っていると、先程のような間違った答えに気付けなかったり、他者からの指摘を受け入れ難くなります。
こうした思考の重要性と知識の危うさを理解してもらうために、この講義では、可能な限り知識を使わずに、1から論理的に積み重ねて行く練習をしました。
知識を大量に仕入れるのも大切ですが、仕入れた知識を実際に使って分析する練習をしてください。それが教養 liberal arts に繋がります。
そして、そうした論理的な思考によって得られた結論に対しても、一歩退いた姿勢でいることが大切です。
なぜならば、論理的に考えて行く過程で、結論に関係のなさそうに見えることは、切り捨てて抽象化しているからです。または、抽象的な物を理解可能な形にするために、都合の良い部分のみを残して具体化しているからです。
既存の知識や枠組みを使うにしても、それは限られた場合に都合の良い結論が得られるだけであり、すべての中で唯一の答えではありません。
想像力を働かせて、物事を断定的ではなく疑いながら、総合的に考えるのが、教養 liberal arts であり、学問的態度です。
まとめましょう。
答えが何か分からないという不安の中で、多様な物事を自由に考えることができるのが、教養 liberal arts です。
「自由」とは、自分の頭で考えることができ、自分のことを自分で決定できることでした。それが、「自由人になるための技芸」です。
また、自分のことを自分で決定できるという意味での「自由」は、1つの考えに縛られることなく、物事を多面的に総合的に考えることができることを意味しています。
1つしか選べなければ、それしか選べないので自由ではありません。
しかし、選択肢が複数あれば、自分で選ぶことができます。
これが自由です。「自らに由って」考えた結果です。
この教養 liberal arts があるからこそ、特定の専門 a discipline を身に付ける意味が増します。
もし専門 a discipline しか知らなければ、その専門の範囲でしか考えることができません。これは非常に、狭い範囲で物事を考えていることになります。これでは、専門に縛られて「自由」ではなくなっています。自分の頭で考えて、自分のことを自分で決定したのではなく、専門 a discipline を選ぶしかなく、専門によって決定しただけなのです。
また、特定分野のみに偏ると、分野を横断する学際的 interdisciplinary な研究についても支障が出ます。教養 liberal arts によって、多様な物事を考える能力が必要になっています。
| かつて小さな講演会で話した「教養 liberal arts について」を掲載しておく。 以下、テキストと同文なので、テキストをダウンロードしている者はそちらを読めばよい。これを読めば、今まで説明して来た「教養 liberal arts が『自由人のための技芸』である」という意味の理解が深まるはずである。 なお、講演の中では一人称に「僕」、人称に「君」を使っているが、これは吉田松陰の考えに基づくものであり、不遜の態度の表れではない。つまり、「下僕」でも「主君」でもなく、どちらが「下」で、どちらが「主」だという概念はない。対等な関係であることを「君」と「僕」という言葉で表している。 「教養 liberal arts について」 今日は、教養について話したいと思います。ここにいる皆さんの多くは、大学への進学を希望していると思いますが、大学へ何をしに行くのでしょうか。 専門知識を身に付けていい会社に入り、いい生活ができるようにするためでしょうか。 それとも、有名大学へ入ることで、自分の頭の良さを誇示するためでしょうか。はたまた、皆が行くから何となく自分も、ということでしょうか。 こうしたものは本来の目的から外れている。大学とは知を希求するところである、といった高尚な志からでしょうか。 大学に何を求めるかは、ひとそれぞれで、何か1つの理想的な目的があると言うのは、現代社会では難しいのかもしれません。しかし、こうした多様な個人個人の思いがあることを考慮したとしても、敢えて大胆に目的を設定したいと思います。 大学へ行く目的とは、教養の修得だと。大学では何よりも教養を身に付けるために行くところだということです。 その理由は、教養が経済的な価値や社会的な価値を超えた真の価値を持つからです。 では、君達に問いたいと思います。教養とは何でしょうか。 教養とは何かと言われても、すぐにこうだとは言えないでしょうから、教養がある人を思い浮かべてみます。 物知りな人を教養がある人だと言う場面を見たことがあるのではないでしょうか。それでは、博識であることが、教養があることなのでしょうか。しかし、物事を色々知っている人でも、何だか馬鹿に思えてしまう人は多くいます。 だとすると、博識だけでは教養があるとは言えないような気がしてきます。 色々な事を知っているのは当然として、様々な事を考えることができる人を見ると、教養のある人だと思えます。なるほど、教養があるとは、知識を単にため込むことではなく、「自分の頭で考える」ことができるということが言えそうです。 教養が「自分の頭で考える」ことである。 これ自体は、なるほどそうだとうなずける定義だと思います。現代社会では既存の知識では対処しきれない問題が多く、考える力が必要だ、とか煩く言われていますし、「自分の頭で考える」ことの大切さは、君達の頭にも刷り込まれていると思います。 では、「自分の頭で考える」とは何なのでしょうか。 皆誰しもが何かしらを考えているものです。全く何も考えていない人というのは、中々いないのではないかと思います。浅はかな行動をする人がいたとしても、その人に聞けば、一応は「自分の頭で考える」ことをした結果の行動だと答えるはずです。そういった状況を指して、考えることが足りなかっただけだと言って終わらしてしまうのは簡単ですが、「自分の頭で考える」という言葉をもう少し丁寧に解釈する必要があるかと思います。 次の高校野球の試合の話を聞いて君達は「自分の頭で考える」ことについて何を思うでしょうか。 今、9回裏2アウト、3対0であなたの高校は負けています。 バッターは1番です。ヒットで出塁しました。2番はフォアボールで出塁できました。2アウト2塁1塁です。3番は打ち上げてしまいますが、フラフラっと上がったボールがポテンと落ちて何とかヒットで続きます。 何と3対0で負けていますが、9回裏2アウト満塁です。 しかも4番バッター。この4番が満塁サヨナラホームランを打ち、まさかの逆転勝利。 奇跡のようなお話です。 そこで、勝利した高校の生徒で観戦していたフミさんとカズ君が話しています。 フミさんは、「皆が頑張ってきたのを神様が見ていてくれたんだ。神様が起こしてくれた奇跡だわ。こんな奇跡的な場面が見れて感動したわ」と泣きながら言いました。 カズ君は、そんなフミさんに対して、「2アウトとはいえ、1番からの連続出塁とホームランの確率を考えれば、滅多に起きないとしても、一応起き得ると言える。これを奇跡と表現するなら奇跡でもいいけど、数字上は起こり得ることなのに、そんなに興奮するなよ」と言います。 フミさんは、「まるで物語のような奇跡が起きたのに、水をささないで」と怒ります。 カズ君はやや呆れながら、「だから、確率上は低いけど、高校野球という身体も技術も成熟していないことを考えれば、まだ有り得る話なのだから、そこまで大げさに言わなくてもいいだろ」と返します。 二人の意見は、平行線のまま交わりませんでした。 この小話は、フミさんが神様を信じる信心深い人である、または、何にでも何かしらのたいそうな価値を見出そうとする文学少女である、といったことや、カズ君は、数字が大好きで何から何まで計算して冷静に判断しようとする合理的な人である、または、女には持てない冴えない奴である、といったことを言いたいのではありません。 この話では、フミさんもカズ君も「自分の頭で考える」ということをしているように見えます。どちらが間違っており、どちらが正しいということはありません。「自分の頭で考える」ことをした結果、二人の意見はぶつかり合い、感動を共有できず、むしろ険悪になってしまっています。 「自分の頭で考える」ことは人と壁をつくることになるのでしょうか。 もちろん違います。これは、本当の意味で「自分の頭で考える」ことができていないからです。 どういうことかと言えば、「自分の頭で考える」とは、「考えるべき対象をどう考えるかを自分で選ぶ」ことだからです。 フミさんもカズ君も「考えるべき対象をどう考えるかを自分で選ぶ」ことができているとは言えません。フミさんは、確率上滅多に起きないことを感動的な奇跡としか考えられていません。カズ君は、感動的で奇跡のようなことを確率上の滅多に起きないこととしか考えられていません。お互いに、別の見方ができることを受け入れていません。 「考えるべき対象をどう考えるかを自分で選ぶ」ことができれば、相手の異なる考えにも共感が示せるはずなのです。 しかし、フミさんもカズ君も、自分の考えに対する盲目的な確信に縛られており、視野が狭くなっていることに気付いていないのです。 これでは「自分の頭で考える」ということができていません。 自動的に正しいと信じて来たことをそのまま適用しているだけです。 反射と変わりません。 食べ物を見ればよだれが出る。痛ければ叫ぶ、泣く。自分の信念に合うように、物事を解釈する。 こうした性質は、おそらく人間の「初期状態」と言えると思います。 人間とは、幸か不幸か、すべてを認識し解釈する意識も、すべてを感覚する肉体も、常に「自分」を中心に働きます。どうしても「自分」が先ず何よりも最初に在って、「自分」を第一に思ってしまうものなのです。 人間の「初期状態」とは、「自分」を中心に考えることで、盲信と偏見の下にすべてを考えてしまうことです。 こうした自分中心的な「初期状態」でも一応は考えているとも言えます。しかし、「自分の頭で考える」ことはできていません。ただ「初期状態」の命令に従っているだけです。 「自分」の感情と欲求が、物事の順序を決定しています。 このことから分かる通り、この「初期状態」は、僕達を支配します。 フミさんは、合理的に「自分の頭で考える」ことができないので、感動さえできれば何でもよしとして、高い壺を買ったり、よく分からない教えを聞いて実践して幸せを感じるかもしれません。傍から見れば、それは偽りの幸せとしか言えないような状態でも彼女は幸せなのです。 一方、カズ君は、物事を感動的に「自分の頭で考える」ことができないので、何でもかんでも数字上は有り得る、これは無駄だからやらない、感動話では腹はふくれないと言い続けるかもしれません。物質的に豊かな生活を送れて、その意味では幸せになれるでしょうが、心を揺さぶるような出来事の素晴らしさが分からずに、不幸とも言えます。 他にも「初期状態」では、お金持ちになりたいという欲求に支配されれば、お金を稼ぐこと以外に目が行かなくなります。 有名になりたい、尊敬されたいという欲求に支配されれば、敬意を表されるかどうかが気になって仕方なくなります。 「自分の頭で考える」ことができず、「初期状態」のままだと、いくら稼いでも、いくら尊敬されても満足できずに、もっともっと、足りない足りないと欲求は膨れ上がって行きます。 そして、いつまでも充たされた気持ちになれず、辛く感じることになります。僕の人生はこんなのでいいのだろうかと。 「初期状態」とは、刹那的に自分に幸福をもたらすことができても、最終的には不幸へと誘うものの可能性もあることが分かります。 それでは、どのようにして「初期状態」から脱することができるのでしょうか。 もう分かりますね。 「自分の頭で考える」ことです。 つまり、「考えるべき対象をどう考えるか自分で選ぶ」ことです。 でも、なるほど確かに「自分の頭で考える」ことは大切だ、と分かったところで、どのようにすれば「自分の頭で考える」ことができるようになるのかが分からないと意味がありません。 「自分の頭で考える」ことができるようになるには、盲信と偏見から脱しないといけません。 これを可能にするのは、「知識」です。 僕達は、「自分の頭で考える」ことができるように、この確かな「知識」を日々勉強しているのです。 学校のお勉強はつまらない、学問の「知識」は専門的過ぎて実社会で何の役に立つかよく分からない。こうした声はよく聞きますが、「知識」は、僕たちを盲信や偏見から解放し、物事を「自分の頭で考える」ことができるようにしてくれているのです。 「知識」は、「初期状態」から「自由」になり「自分の頭で考える」のに必要不可欠なものです。 でも、話を思い返すと、「知識」を多く持っていること、博識であることは、教養があることまでを意味していませんでした。 そうです、「知識」があるだけでは、「自分の頭で考える」ことにはならないのです。 「知識」が増えるにつれて、そして、「知識」が持つ正確さや問題解決の力を経験するにつれて、「知識」に魅了され、その「知識」を以って物事を考えるようになります。 学術的に分析して、抽象的な議論をして、僕達は、無批判にAだからBという定理や法則を何でも適用して分かった気になりがちです。 目の前に確かに存在する現実に注意を払わずに、多様な世界を論理でぶった切って型にはめてしまいます。 特に自分の得意な専門的な「知識」を基準にしてしまいます。 これでは、「自分の頭で考える」のではなく、感情や欲求が知識に変わっただけで「初期状態」へと再度戻ってしまっているのと同じです。 それでは、「自分の頭で考える」ためには、「知識」だけでは駄目なのだとしたら、どうすればよいのか、と思うかもしれません。 精神論に聞こえるかもしれませんが、心の余裕と自制心です。 「自分」の感情や欲求によって物事の価値や順序を自動的に決めるのではなく、「考えるべき対象をどう考えるかを自分で選ぶ」という心の余裕があれば、「知識」を基にして、物事を違った視点から見ることができます。物事が異なるように見えれば、自分にとってその物事の位置付けも変わります。 そうした多面的な見方をすることで、自分にとって、その物事の真の価値が見えてくるものです。 こうした心の余裕は、常にあるとは限りません。 僕達は常に盲信と偏見のあの「初期状態」に戻るようになっているからです。 人間、易きに流れるものです。 「自分の頭で考える」ことの辛さに負けて、「初期状態」に戻って、感情や欲求によって物事の序列が自動的に決まる楽な状態につい戻ってしまうことだってあります。 「初期状態」は、何もかもが勝手に決まる楽な状態なのです。だから、自制心をもって、楽な「初期状態」ではなく、辛いかもしれないが「自分の頭で考える」ことを心掛け、物事の価値を見極めて行かないといけません。 もし確かな「知識」を持っており、なおかつ、心の余裕と自制心があれば、「自分の頭で考える」ことができます。 そうすれば、何に意味があって価値があるのか、何に意味がなく価値がないのかが、自動的に決まるのではなく、「自分」で選ぶことができます。 これが「自由」です。 「自分」で自分のことは決めるという「自らに由る」ことです。 そして、「初期状態」は決して「自由」ではありません。自分で選んだ気がしますが、盲信と偏見によって、自分の判断基準を狭くして自動的に決まっているだけで、「自分」で選んでいません。 「自由」を得ることは、非常に難しいのです。 でも、「自由」はとても価値のあるものです。「自分」で自分のことが決められるからです。 このような真の意味での「自由」は、お金では買えませんし、偉くなったからといって得られるものでもありません。 「自分の頭で考える」こと、つまり、「知識」を利用しつつも「考えるべき対象をどう考えるか自分で選ぶ」ことでのみ獲得できるものです。 そして、これが、教養と呼ばれるものです。 教養があれば、孤独で偏狭な自分だけの世界から「自由」になり、異なる他者を理解できます。 また、色々な物事に価値を見いだせて、人生を豊かにしてくれます。 これが、最初に述べた教養が経済的価値や社会的価値を超えた真の価値を持つ所以です。 もちろん、大学に行けば、皆が皆、教養を修得できるわけではありませんし、大学だけで教養を完全に修得できるわけでもありません。 人生ずっと教養を磨くことになります。 でも、大学は、教養を、少なくともその基礎を身に付けることができる環境を用意してくれています。 それを上手く利用できるかどうかは、「自分」次第です。 フミさんのように世界を感動的な奇跡として捉えることも、カズ君のように世界を合理的な方法で処理していくことも、「自分」で決めることができ、状況に応じて変えることができます。そして、どちらにしても「自分」以外の他者への共感を持てるようになってください。 それが教養です。 |
5 おわりに
以上で、31章、序章も入れれば全32章にわたる講義を終えます。
第 I 部 論理的思考の基礎を学びました。正しく考えるための基礎的な能力になります。
第 II 部 論理的な問題解決では、論理的思考に基づいた実践方法を学びました。
第 III 部 教養と学問・科学では、論理的思考に基づいた学問的・科学的研究が何故正しいと認められるのかということを学びました。そして、学問の専門分化と教養の関係性についても学びました。
教養 liberal arts を身に付けるための思考訓練の方法は、第 I 部と第 II 部が参考になるはずです。
これは、基本的な思考方法と問題分析の方法です。専門分野 disciplines の研究になっても、この思考方法が基礎となります。そして、この基礎的な思考法に各専門の規則を加えていくことになります。
また、第 III 部では、論理的思考に基づく学問的・科学的思考の原則を学びました。
教養 liberal arts と専門 disciplines の関係を見たので、日頃の勉強が全体の学問の中でどういった位置づけにあるのかが、大まかにですがつかめたはずです。
講義で学んで来た論理的思考とその実践、科学的・学問的思考に基づいて、日々の疑問や勉強で教養 liberal arts を深めて行ってください。
そして、教養 liberal arts を身に付けることが、高校生や大学生に先ず課された使命です。
高校生の皆さんは、文科系・理科系の分類や入試科目に絞った勉学ではなく、幅広く学ぶようにしてもらいたいです。
また、大学生でも、自分の専門分野だけではなく教養を大切にすることを願っています。
この教養の養成は、社会人になって働き始めても、周囲の人と上手くやっていくのに非常に役立ちますし、何よりも、あなたの人生を「豊かに」してくれるはずです。
ご清聴ありがとうございました。
前頁:第30章 学問の専門分化
ページトップへ:第31章 教養と学問
次頁:引用・参考文献