前頁 |▼| 次頁
第20章 論理ピラミッドの基本
論理ピラミッドは、「現象型」の問題を分析するための道具です。
論理ツリーは「困ったこと」と原因が1対1で対応しやすい「発生型」の問題に対して、因果関係図は連続的に現れる「困ったこと」の因果関係が絡み合う「構造型」の問題に対して、それぞれ有効な道具でした。
最後に、「発生型」の問題のような「困ったこと」と原因が1対1に対応するような問題とは異なり、複数の「困ったこと」が連続的に現れるという点では「構造型」の問題と共通するが、因果関係が明確にあるような構造になっていないような問題があります。
こうした「現象型」の問題の本質的原因をどのように分析するときに活躍するのが、論理ピラミッドです。これから3章に渡って論理ピラミッドについて学びます。
まずは、論理ピラミッドが一体何なのかを理解することから始めます。
| 目次 |
| 1 論理ピラミッドとは 2 トップダウン(逆算)方式 3 ボトムアップ(積み上げ)方式 4 論理ピラミッドの作り方 5 注意点 6 まとめ テキストのダウンロード[詳細] 通常版 既述版 配布資料 |
| ADs |
1 論理ピラミッドとは
論理ピラミッド、または、ピラミッドストラクチャーとは、問題の分析の他にも、論理的な文章や発表を組み立てるのに役に立つ道具です。具体的な事実や客観的な事柄をまとめて抽象的な次元まで積み上げることが主な使い方になります。英語では、pyramid structure と言われます。
「ピラミッド」という言葉から、エジプトにある四面体のピラミッドを思い浮かべる人が多いでしょう。その名の通り、論理ピラミッドは、ピラミッドを正面から見たような、三角形の構造をとります。
論理ピラミッドについては、既に少し触れています。第12章 目的と手段 4 まとめ 論理的主張と目的 ― 手段で、論理的な主張において、結論と前提の関係が明確で、目的と手段が提示されていることが大切だと説明しました。
実はこのとき、論理ピラミッドのような図で表していました。
図12.4.論理的な主張と目的と手段 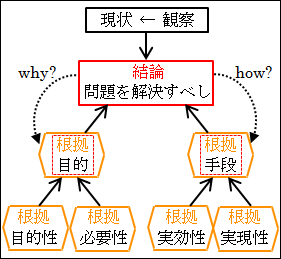
このように、頂点が細く下に行くほど広くなっていく形から、論理がピラミッドのように構築されているように見えるため、論理ピラミッドと言います。
他にも、第13章 演繹法と帰納法の絡み 1 絡み合いでは、実例を使って、論理ピラミッドを作りました。
図13.1.演繹法と帰納法の絡み 画像クリックで拡大 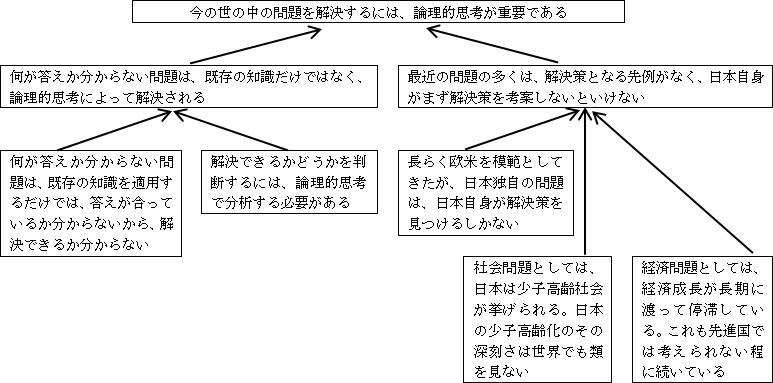
このように、論理ピラミッドは、上から下に行くほど枝分かれしていくように描きます。
これは、論理ツリーが右から左に枝分かれするのに似ていますね。
図からも分かる通り、一番上、頂点にある箱は基本的には1つです。
ここには、最も抽象的・一般的・普遍的な命題が置かれます。
これを主命題とか、メイン・メッセージや主メッセージなどと呼びます。あるいは、最上位命題とも言います。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 
そして、その最上位命題の下側に、その命題をより具体的な構成要素に分けます。
これを副命題やサブ命題、サブ・メッセージと呼びます。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 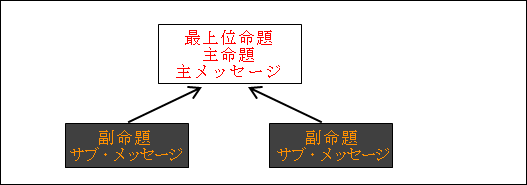
命題をいくつの要素に分解できるかは、それぞれの命題で異なります。
副命題から主命題へと矢印(→)を伸ばします。これは必ずしも因果関係を表しているわけではなく、論理関係があることを表しています。
下側に分解された命題や概念をさらに下側に分解していきます。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 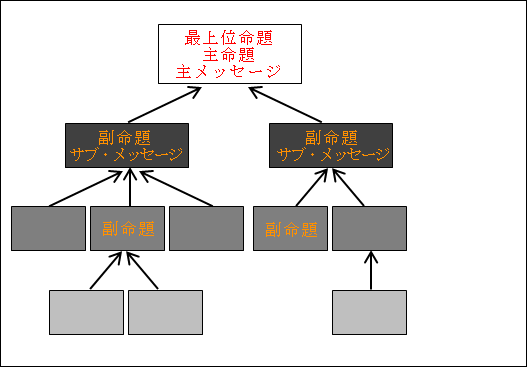
命題を分解してい行くことを何度か繰り返していきます。何回繰り返せばよいかも命題によって異なります。
そうすると、一番上が最も一般的・抽象的・普遍的な命題であり、下に行くに従って、個別的・具体的・特殊的なな命題になって行きます。
そして、普通、論理的な主張では、抽象的な命題が結論として現れ、具体的な命題が前提として現れることになります。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 
一番下にある命題は最下位命題と呼びます。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 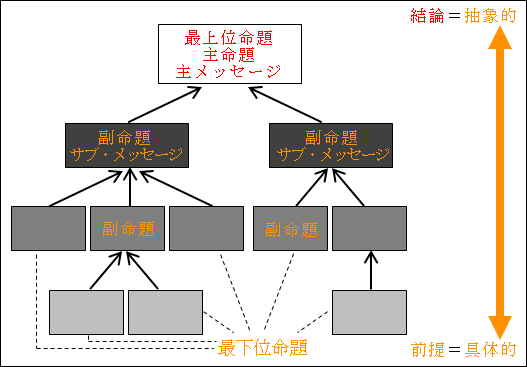
最下位命題が一番下にあることから分かる通り、最も具体的になります。
ですから、この最下位命題には、単なる事実や誰が見ても「そうだ」と言えるような客観的な事柄が来ることが多いです。
この最下位命題が、論理の出発点であり、最初の前提であり、誰もが認める事実や根拠になります。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 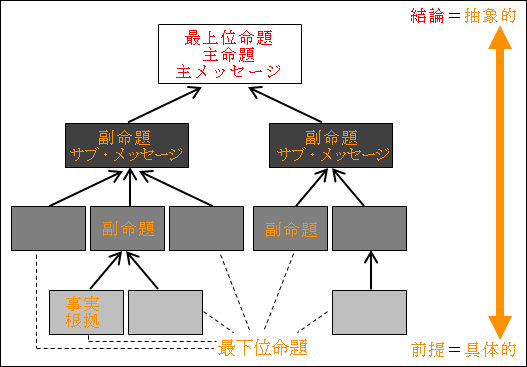
なお、下位命題が同じ抽象度であっても、上位命題から枝分かれして、異なる深さの階層に置かれることになっても構いません。
そして、各行には名前がついており、上から順に第1階層、第2階層、第3階層、第4階層…と呼ばれます。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 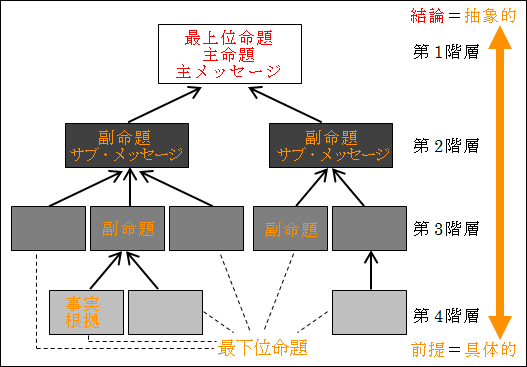
矢印の上側を上位命題、下側を下位命題と呼びます。これは相対的な捉え方になります。
第1階層から見れば、最上位命題でもある第1階層のみが上位命題で、他はすべて下位命題となります。
第2階層から見れば、第1階層は、上位命題になり、第2階層は下位命題となります。
しかし、第3階層と比べれば、上位命題は第2階層になり、第3階層が下位命題になります。
このようにして、具体的な要素から、本質的な原因や問題を抽象化して総合することで、総合的論理ピラミッドは構築されています。
論理ピラミッドを見れば、主張の結論とその根拠が何なのか、どのような論理展開や論理構造になっているのか、といったことが視覚的に分かります。
そして、結論が正しいか否かは、最下位命題から出発して、各階層が正しく繋がっているかを確認することで確かめることができます。
このように、論理の繋がりや構造が一目でわかる論理ピラミッドは、「現象型」の問題の分析、論理的な主張や文章の作成、その発表、などなど様々なことに役立ちます。
以上のことを踏まえると、論理ピラミッドの特徴が分かります。
まず、最上位命題は、最も一般的・抽象的な命題で、下位階層に行くほど、個別的・具体的な命題になります。
このことから、論理ピラミッドの原理として、最上位命題は、最下位命題を含むすべての下位階層の命題を内包しているのが分かります。
そして、最下位命題は最も個別的・具体的な命題になります。よって、論理の出発点となり、根拠たる前提として、誰もが認める事実や客観的な事柄が置かれることになります。
論理ピラミッドの特徴
|
論理ピラミッドが一体何なのかが分かったところで、論理ツリーと非常に良く似ていることに気付きます。
論理ピラミッドは縦に下に伸ばしていくのに対して、論理ツリーは横に右に伸ばしている点で異なりますが、上位階層と下位階層の関係は非常に似ています。
実際、論理ツリーの作り方にボトムアップ方式とトップダウン方式という2通りあったように、論理ピラミッドを作るときにも、ボトムアップ方式とトップダウン方式の2通りあります。
逆に、似ていないところもあります。
論理ツリーを作る際には、枠組み(フレームワーク)と MECE(ダブりなくモレなく)という二本柱がありましたが、論理ピラミッドでは、枠組みと MECE という柱は、そこまで重要になってきません。
そして、論理ツリーも論理ピラミッドも、ボトムアップ(積み上げ)方式とトップダウン(逆算)方式の2通りあるという点では共通しても、向き不向きの点で異なります。特に問題を分析する際に、その向き不向きが顕著になります。
論理ツリーは、トップダウン方式が適していました。
「発生型」の問題は、単発的に現れる「困ったこと」と原因が1対1に対応していることが多く、それを上手く分析するためには、ダブりなくモレなく(MECE)分解して原因を特定することが必要でした。
したがって、個別的で具体的な事実を積み重ねて行くよりも、適切な枠組みを一般的で抽象的な命題に適用して MECE に個別的で具体的な要素に分解する方が適切になりました。
個別的で具体的な事実を積み重ねて行くと、どうしてもモレが生じたり、ダブりが生じたりすることが多くなるからでした。
これに対して、論理ピラミッドで問題を分析する際には、ボトムアップ方式が適しています。
複数の「困ったこと」が現れるため、トップダウン方式で逆算して行くのが困難になります。トップダウン方式では、一般的・抽象的な命題が定まっており、そこから逆算して個別的・具体的な事実へと掘り下げます。これでは、複数の「困ったこと」が存在していることが分かっているだけでは足りず、全体として何に困っているのかが明確ではないと問題と原因が明らかにできません。
つまり、トップダウン方式では、複数の「困ったこと」が引き起こしている本質的な問題や原因が分かっている必要があるということになります。これでは、本末転倒です。本質的な問題や原因が分からないから、問題を分析しようとしているのに、それが分からないと分析ができないという状況になってしまいます。
ですから、論理ピラミッドで問題を分析する際には、複数の「困ったこと」から積み上げて、一体何が最も「困ったこと」であり、原因なのかを抽象化して行く方が適していることになります。
と言っても、論理ツリーならトップダウン方式だけ、論理ピラミッドならボトムアップ方式だけという必ず守らなければならない縛りではありません。論理ツリーなのにボトムアップ方式で、論理ピラミッドなのにトップダウン方式で、問題を分析できる場合もあります。また、問題を分析している最中は、どちらか一方だけではなく、トップダウンとボトムアップの両方を適宜使うことも多いです。
向き不向きの傾向を述べただけなので、問題の種類や持っている情報によって臨機応変に切り替えてください。
ボトムアップ方式とトップダウン方式という話題が出た所で、論理ピラミッドにおけるトップダウン方式とボトムアップ方式の使い方を見てましょう。
2 トップダウン(逆算)方式
ボトムアップ(積み上げ)方式での論理ピラミッドの作成方法については、次章の「現象型」の問題でゆっくりじっくりと説明します。ですから、先ずは、トップダウン(逆算)方式による論理ピラミッドの作り方を説明します。
確認ですが、トップダウン方式、つまり、逆算方式は、一般的・抽象的な事柄から個別的・具体的な事柄を考えて行く方法でした。
このトップダウン方式を論理ピラミッドに適用すると、いわゆる「始めに結論ありき」の論理構築になりやすいです。
なぜならば、一般的・抽象的な事柄から論理を開始するためです。
図20.1.論理ピラミッドの概念図を観てください。
図20.1.論理ピラミッドの概念図 画像クリックで拡大 
論理ピラミッドの最上位階層にある命題は結論でした。
トップダウン方式ということは、この最も一般的・抽象的な最上位階層の結論から論理を構築していくことになります。
もちろん、結論だけでは論理的な主張にはなりません。論理的な主張と言うためには、結論を支える根拠たる前提が必要でした。ですから、トップダウン方式では、結論を上手く支えるような前提になってくれる事実や事柄を探して行くことになります。
このことを踏まえると、トップダウン方式で論理ピラミッドを作る場合は、最初から結論が明確であり、確固たる根拠がある程度存在しているときに向いていることが分かります。
それでは、実際にトップダウン方式で論理ピラミッドを作ってみましょう。
(20.1)を見てください。これは(13.1)のAの主張を結論と前提にバラしたものです(第13章 演繹法と帰納法の絡み合い 1 推論の絡み合い参照)。再現するだけですから、論理ピラミッドを簡単に作れるかと思います。
(20.1)以下の情報から、「今の世の中の問題を解決するには、論理的思考が重要である」という主張を構成する論理ピラミッドを構築せよ。
|
結論として「今の世の中の問題を解決するには、論理的思考が重要である」という主張を論理構築したい場合、前提として何が必要になるでしょうか。
演繹法の定言三段論法で考えます。
| 定言三段論法 <大前提> M - P <小前提> S - M [結論] よって、S - P |
大前提「M ならば、論理的思考が重要である」ことと小前提「今の世の中の問題を解決するには、M である」ことが必要になります。
Mは、大前提と小前提を繋ぐのに必要な共通概念ですが、まだ分からないので、便宜上 M と置いています。
図20.2.演繹法による結論の導出
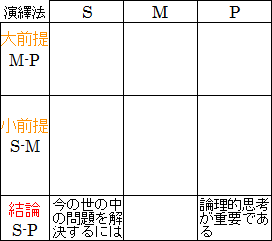
もし帰納法で考えると、「今の世の中の問題を解決するには、論理的思考が重要である」と言える具体的な事例を集めることが必要になります。
さて、(20.1)から、持っている情報を見ると、大前提の後件「論理的思考が重要である」ことに関係しそうなものは、
| (1) | 何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される |
| (2) | 何が答えか分からない問題は、既存の知識を適用するだけでは、答えが合っているかどうか分からないから、解決できるか分からない |
| (3) | 解決できるかどうかを判断するには、論理的思考で分析する必要がある |
さらに、小前提の中の概念「今の世の中の問題」に関係しそうなものは、
| (4) | 最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない |
| (5) | 社会問題としては、日本は少子高齢社会が挙げられる。日本の少子高齢化のその深刻さは世界でも類を見ない |
| (6) | 経済問題としては、経済成長が長期に渡って停滞している。これも先進国では考えられない程に続いている |
| (7) | 長らく欧米を模範としてきたが、日本独自の問題は、日本自身が解決策を見つけるしかない |
共通概念である M となりそうなものを、(4)~(7)のグループと、(1)~(3)のグループの中から見つけます。
共通概念である M を見つけたいのだから、似たことを述べている命題を見つけ出せばいいです。
そこで、
| (1) | 何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される |
| (4) | 最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない |
(1)の「何が答えか分からない問題は、既存の知識だけではなく」の部分と、
(4)の「解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」の部分は、
表現こそ違いますが、非常に似たことを言っています。
つまり、「何が答えか分からない」ことは、「解決策となる先例がな」いことと言い換えられます。
また、「既存の知識だけではなく」ということは、「日本自身がまず解決策を考案しないといけない」ことと同じ意味になります。
これが共通概念 M だと考えれば、定言三段論法にしっかりと当てはめることができます。
したがって、結論「今の世の中の問題を解決するには、論理的思考が重要である」を導くための前提に、大前提(1)「何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される」、小前提(4)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」が置かれることが分かりました。
図20.2.演繹法による結論の導出
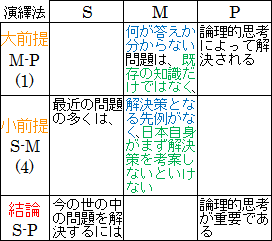
論理的な推論では、「S - M」と記号で表してまったく同じものが出てきますが、日常における実践では、このように名詞や文構造が微妙に異なるものになることが多いです。ですが、表面上の違いに惑わされずに、意味する内容を理解して、しっかりと論理を見極められるようにならないといけません。
それでは、大前提(1)「何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される」ことを述べるには、前提として何が必要でしょうか。
演繹法の定言三段論法で考えると、大前提「M は、既存の知識だけではなく、論理的思考によって解決される」と、小前提「何が答えか分からない問題は、M である」ことが必要になります。
帰納法で考えると、(1)「何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される」ことの具体例が必要になります。
図20.3.帰納法による大前提の導出
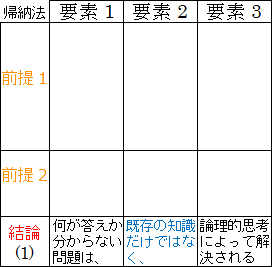
もう(4)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」は使っているので、残りの(2)~(3)、(5)~(7)から適当な命題を探します。
(2)と(3)を見てみると、
| (2) | 何が答えか分からない問題は、既存の知識を適用するだけでは、答えが合っているかどうか分からないから、解決できるか分からない |
| (3) | 解決できるかどうかを判断するには、論理的思考で分析する必要がある |
この2つの命題を併せた帰納法による推論を行えば、(1)「何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される」ことを導けると判断できます。
なお、(2)の「既存の知識を適用するだけでは、答えが合っているかどうか分からないから、解決できるか分からない」の部分と、
(3)の「解決できるかどうかを判断するには」の部分は、
表現が違いますが、(1)では「既存の知識だけではなく」と要約されています。
図20.3.帰納法による大前提の導出
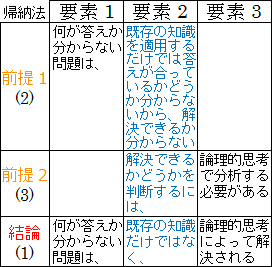
次に、小前提(4)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」ことを述べるには、前提として何が必要でしょうか。
演繹法の定言三段論法で考えると、大前提「M は、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」と、小前提「最近の問題の多くは、M である」ことが必要になります。
図20.4.演繹法による小前提の導出
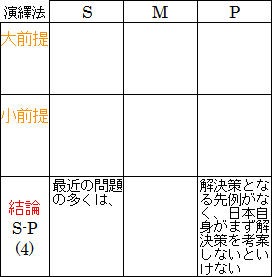
帰納法で考えると、(4)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」ことの具体例が必要になります。
(1)~(3)は使ってしまったので、(5)~(7)の中から適切な命題を探し出して前提とすることになります。そこで、(5)~(7)の3つを見てみると、
| (7) | 長らく欧米を模範としてきたが、日本独自の問題は、日本自身が解決策を見つけるしかない |
図20.4.演繹法による小前提の導出

しかし、肝心の小前提「最近の問題の多くは、M である」に当てはまるものがありません。
つまり、共通概念 M として「長らく欧米を模範としてきたが、日本独自の問題」と似たものが必要なのに、それが見当たらないことになります。
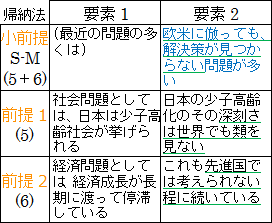
ここで、「長らく欧米を模範としてきたが、日本独自の問題」は、(5)「社会問題」と(6)「経済問題」を帰納法的に抽象化した概念と言えることに気付きます。
| (5) | 社会問題としては、日本は少子高齢社会が挙げられる。日本の少子高齢化のその深刻さは世界でも類を見ない |
| (6) | 経済問題としては、経済成長が長期に渡って停滞している。これも先進国では考えられない程に続いている |
表現をこなれた日本語にすると、「欧米に倣っても、解決策が見つからない問題が多い」となります。
図20.5.帰納法による小前提の前提の導出
これは、問題文に与えられた事実そのものではなく、自分で推論して補足したものになりますが、これを導くために新たな事実や事柄を勝手に持ってきたわけではないので良しとします。
このようにして、小前提(4)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」ことが導けました。
図20.4.演繹法による小前提の導出
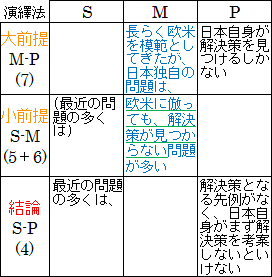
このように、トップダウン方式で論理ピラミッドを作る場合、結論から始めて、それに合う事実や事柄を前提に配置できないかを考えながら、探していくことになります。
図20.6.トップダウン方式による論理構築 画像クリックで拡大

ただし、最上位命題の結論から根拠たる前提を探すと述べたことから分かる通り、最初から都合よく必要十分な根拠が揃っているとは限りません。
そのときには、足りない根拠を再度探して来るか、または、手持ちの根拠だけで最上位命題たる結論になるように修正する必要があります。
でも、この結論に合わせて根拠を不足なく揃えることや、結論を根拠に合わせて修正することって結構難しいんですね。
こうした誤りを犯しやすいことは、第11章(補講) 論理的思考の誤謬で触れたことです。
「結論ありき」ということから分かる通り、最初から結論があります。その結論に引っ張られて、都合の良い事実や事柄ばかり集めてしまい、都合の悪い事実を無視してしまう確率が高くなります。人間、「これだ!」と思い込むと、それに向かって突っ走ってしまいがちです。
さらに酷いことになるときもあります。
最初に考え付いた結論が自分の信念から来るものだった場合、「結論を修正したくない、何とかこの結論に導きたい」という思いが出てきます。そうすると、論理的な主張と言うには明らかに根拠が不足しているのに、結論を修正せずに最初に抱いた結論に無理矢理繋げたりすることがあります。これでは、屁理屈にしか聞こえない主張になります。また、先程は都合の悪い事実を無視してしまうことが、不注意や思い込みで結論に引っ張られてしまったために起きていましたが、結論に無理矢理繋げるために意図的に無視したりする場合もあります。こうなると、議論しているときに手が負えなくなる確率が高いです。「結論ありき」な上に、その結論を死守したいがために、そういうことを意図的にしているのだから、こちらが論理的に相手の論理の欠陥を指摘しても、相手は訂正せずに、強弁しがちになります。
これは結構見かけますね。
ニュースを見ていても政府の説明が何だか質問に答えていなかったりすることがありますが、「結論ありき」で話を進めているからと言えます。政府批判だけではフェアではありません。新聞や報道番組の話も、最初から「結論ありき」で考慮すべき事実を無視したり、耳に心地よい言葉で誤魔化して無理矢理結論を導いたりしていることがあります。
何事も、根拠たる前提になっている単なる事実だけではなく、明示されないが確かに結論を支える前提の1つとなっている思想や依拠する権利団体・利益集団が何なのかという隠れた前提を考慮する必要があります。そうしたことを総合的に考慮して、相手の主張が是なのか非なのかを判断する必要があります。
皆さんがトップダウン方式で論理ピラミッドを作るときには、このような状況に陥らないように気を付けてください。
以上、論理ピラミッドをトップダウン方式で作る場合について見ました。
「始めに結論ありき」ということからも分かるように、確固たる根拠がある程度あり、直観的にも「結論はこれだ」と思えることができる主張を論理的に組み立てるときに効果的です。
3 ボトムアップ(積み上げ)方式
トップダウン(逆算)方式が一般的・抽象的な事柄から個別的・具体的な事柄を考えて行く方法だったのに対して、ボトムアップ(積み上げ)方式は、個別的・具体的な複数の事柄をまとめて一般化・抽象化して行く方法です。
先程のトップダウン方式で論理ピラミッドを構築するときは、「始めに結論ありき」のように、一般的・抽象的な結論から、必要な個別的・具体的な根拠たる前提を配置して行きました。
その逆の方法であるボトムアップ方式で論理ピラミッドを構築するときは、個別的・具体的な事実や事柄を前提として、その根拠たる前提から一般的・抽象的な結論を導くことになります。
2 トップダウン(逆算)方式では、「結論ありき」で「今の世の中の問題を解決するには、論理的思考が重要である」という結論を導くために、必要な事実や事柄を根拠たる前提となるように、上手く配置していきました。
今回は、ボトムアップ(積み上げ)方式で「今の世の中の問題を解決するには、論理的思考が重要である」という結論を導く過程を見てみます。
なお、(20.1)と同じ事実や事柄なので、答えが分かっておりそれこそ「結論ありき」でボトムアップ方式をしているように感じるかもしれませんが、次の章で、ボトムアップ方式による「現象型」の問題の分析を行うので、とりあえずここでは、ボトムアップ方式をどのように行うかを確認することに集中してください。
(20.2)以下の情報から、導かれる結論は何か。論理ピラミッドを構築して考えよ。
|
ボトムアップ方式では、個別的・具体的な情報から何かしらの結論を導くわけですから、共通点や関連性に注目して、いくつかのまとまりに分類します。これをグルーピングと言います。英語の group が「集団にする」という意味があることからも分かりやすいかと思います。
(20.2)の(1)~(7)をグルーピングすると、次の2つのまとまりに分けられます。
まず、(1)~(3)は、「何が答えか分からない問題」に対して、「どのように解決できるのか」について述べています。
そして、その鍵となるのが「論理的思考」だと述べています。
このことから、(1)~(3)は、(A)「論理的思考の重要性」について述べたものとして括れます。
図20.7.グルーピング
|
続いて、(4)~(7)は、「日本の問題がどういったものなのか」について述べています。
いろいろな具体例が挙げられています。
このことから、(4)~(7)は、(B)「最近の日本の事情と問題」について述べているものとして括れます。
図20.7.グルーピング
|
なお、1つの命題だけで、1つのグループになっても構いません。
また、グループ内で上位命題と下位命題の関係になっている場合もあるので、各グループの抽象度が同じなのか、違うのかも意識しておく必要があります。
それぞれのグループの各命題に注目して、抽象化します。
つまり、グループの各命題を下位命題として、上位命題を抽象化して導きます。
その際には、グループの中にさらにグループができることになります。
それでは、(A)「論理的思考の重要性」について細かく見てみましょう。
(1)は、(2)と(3)を併せた命題だと分かります。
つまり、(1)は、一般性や抽象度について、(2)と(3)よりも高いと判断できます。
そして、(2)と(3)から帰納法的に導いたものが(1)だと判断できます。
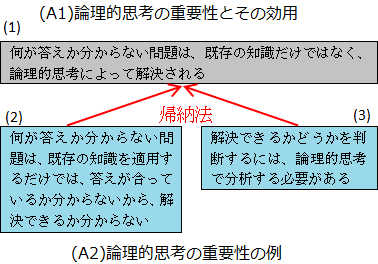
(1)「何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される」ことから、(A1)「論理的思考の重要性とその効用」というグループ名をつけておきます。
(2)と(3)を、(A2)「論理的思考の重要性の例」というグループ名をつけておきます。
図20.7.グルーピング
|
(B)「最近の日本の事情と問題」についても細かく見ましょう。
(4)は、(5)~(7)よりも一般性や抽象度が高いです。
そうすると、(4)と(5)~(7)で別の枠組みに分けられます。
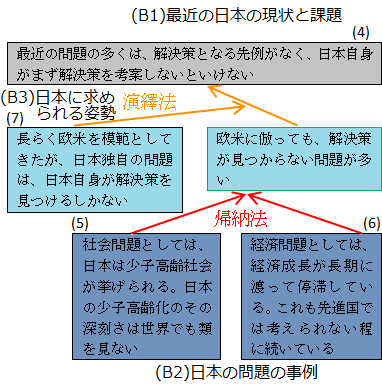
(4)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」ことから、(B1)「最近の日本の現状と課題」というグループ名をつけておきます。
次に、(5)と(6)は、かなり個別的あるいは具体的な事例について述べているのが分かります。
したがって、(5)と(6)をまとめて、(B2)「日本の問題の事例」というグループ名をつけておきます。
最後に、余った(7)「長らく欧米を模範としてきたが、日本独自の問題は、日本自身が解決策を見つけるしかない」ことから、(B3)「日本に求められる姿勢」というグループ名をつけておきます。
図20.7.グルーピング
|
グループ化ができたので、抽象化されたグループ名を命題化します。
命題の定義が、「主語と述語で表され真偽が判定できるもの」なので、命題化は、「主語と述語で表し真偽が判定できる形にすること」になります。
今回は、グループ名が名詞なので、この名詞を命題化することになります。
ただし、グループの中に1つの命題しか存在しない場合は、その命題をそのまま流用することも可能なことが多いです。
まず、(A)「論理的思考の重要性」から考えます。
(A1)「論理的思考の重要性とその効用」は、(A2)「論理的思考の重要性の例」よりも一般性・抽象性の高いものでした。
したがって、(A1)を上位命題(結論)として(A2)を下位命題(前提)として、そのまま帰納法によって導けます。
図20.8.ボトムアップ方式による論理構築 画像クリックで拡大
次に、(B)「最近の日本の事情と問題」について考えます。
(B1)「最近の日本の現状と課題」は、(B2)「日本の問題の事例」と(B3)「日本に求められる姿勢」よりも一般性・抽象性の高いものでした。
(B1)を導くために、(B2)と(B3)が使えそうです。
また、(B1)「最近の日本の現状と課題」は、(4)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」ことのみで構成されているので、(4)をそのまま上位命題として使います。
(B3)「日本に求められる姿勢」も、(7)「長らく欧米を模範としてきたが、日本独自の問題は、日本自身が解決策を見つけるしかない」ことのみで構成されているので、(7)をそのまま下位命題として使います。
(B2)「日本の問題の事例」は、2つの命題(5)「社会問題としては、日本は少子高齢社会が挙げられる。日本の少子高齢化のその深刻さは世界でも類を見ない」ことと、(6)「経済問題としては、経済成長が長期に渡って停滞している。これも先進国では考えられない程に続いている」ことで構成されています。
したがって、(B2)は、(5)と(6)を言い表した命題にしてやる必要があります。
加えて、その(B2)の命題化は、(B3)と合わさって、(B1)を導けるような表現であることが望ましいです。
そうすると、(B2')「欧米に倣っても解決策が見つからない問題が多い」という表現で命題化できます。
以上から、(B1)という結論は、(B2)を小前提、(B3)を大前提とした演繹法によって導かれます。
図20.8.ボトムアップ方式による論理構築 画像クリックで拡大
(A1)かつ(1)である「何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される」と、(B1)かつ(4)である「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」という2つの命題がそろいました。
この2つの命題から、何が言えるでしょうか。
それは、(4=B1)「最近の問題の多くは、解決策となる先例がなく、日本自身がまず解決策を考案しないといけない」ことから、「最近の問題の多くは、何が答えか分からない問題」であることが分かります。
したがって、(1=A1)「何が答えか分からない問題は、既存の知識だけではなく、論理的思考によって解決される」ことから、「最近の問題は、既存の知識だけではなく、論理的思考によって解決される」ことだと言えます。
これでは冗長なので、短く簡潔にしてやると、結論として「今の世の中の問題を解決するには、論理的思考が重要である」ということが導けます。これは(1=A1)が大前提、(4=B1)が小前提の演繹法によって導けます。
図20.8.ボトムアップ方式による論理構築 画像クリックで拡大
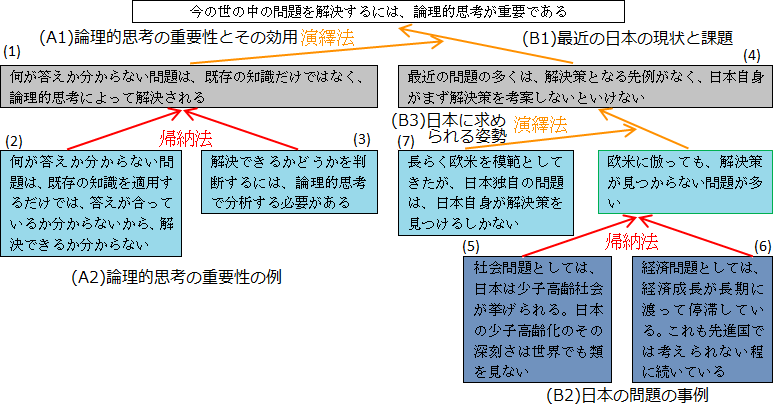
このように、ボトムアップ方式で論理ピラミッドを作る場合、情報を収集して、事実や事柄が集まり、それらを前提にして、結論を導くことになります。漠然とした問題意識を抱いた最初の段階では、結論がどうなるのか分かっていません。
もちろん、あらかじめ確かな事実や事柄などの関連する情報がいくつも存在している場合もあります。
そのような場合には、存在する情報の確かな根拠に基づいて、ボトムアップ方式で結論を導くことができます。
しかし、ボトムアップ方式で結論が導けても、その結論が満足いくものではないかもしれません。
論理の構成が十分に具体的ではなく、結論が本質的でなかったりして、どこか曖昧なとき、「もう少し明確にならないか」と感じることがあります。その際には不足している根拠を考えて情報を収集することになります。これはトップダウン方式のような思考の流れが含まれることになります。そうすることで、より妥当性の高い結論を導くことができます。
なお、実際に複雑な問題を分析するときに、グルーピングを試みれば、まとめ方は十人十色となります。
人によって、どこに共通点を見出すか等は異なりますし、また何を重要だと考えるかも異なるからです。確かに、明らかに突拍子もなく非論理的なまとめ方はダメですが、人によってまとめ方が異なること自体はまったく問題ありません。
4 論理ピラミッドの作り方
トップダウン(逆算)方式とボトムアップ(積み上げ)方式の2つの方法で、論理ピラミッドを実際に作りました。
ここで、論理ピラミッドのボトムアップ(積み上げ)方式で論理ピラミッドの作り方をまとめておきます。
論理ピラミッドの作り方
|
命題を主語と述語で表すのが原則です。
名詞だけでは、何がその名詞に何をしたのか、あるいは、名詞が何に何をしたのか、といったことが曖昧になり分かり難くなるからです。
ただし、最下位命題くらいまで具体的な階層になると、純粋に名詞だけになる可能性もあります。このように、どうしても主語と述語で表すことができない場合は、そのまま名詞だけでも構いません。
グルーピングは十人十色と述べましたが、このグルーピングは個人個人の物の捉え方、まとめかたで変わってきます。
グルーピングは、複数の対象をまとめる、整理する、分類する、といったことをしているので、論理ツリーで利用した枠組み(フレームワーク)が使えそうだと考える人もいるでしょう。もちろん、そのような場合は、既存の枠組み(フレームワーク)を用いて、事実や事柄をグルーピングしても構いません。
ただし、既存の枠組みを使う場合には、その枠組みが本当に使える場面なのか、といったことに注意が必要です。
最後に、上位命題と下位命題の整合性を確認するには、論理ツリーのときと同様に、so what? と why so? が使えます。詳しくは、第16章 論理ツリー - why ツリー - 6 why ツリーの応用で説明したので、上位階層と下位階層の基本的な関係を確認だけしておきます。
トップダウン方式で考えている場合には、「上位階層から見て下位階層は論理的に整合的か」と考えていることになるので、why so? が便利です。
why so? とは、日本語で言うところの「何故そうなのか?」です。
抽象から具体へ、あるいは、結論から前提へという流れになります。
上位階層の命題や概念に対して、「それって、何故そうなのか?」と尋ねれたとき、その原因や理由を答えたり、具体的な事例を挙げたりして答えることになります。
図16.6.why so?
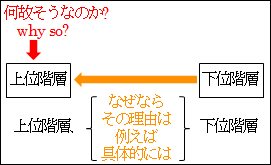
接続的な表現で言えば、「なぜならば」や「その理由は」、「例えば」や「具体的には」といった表現で上位階層と下位階層が繋がるかを確認することになります。
ボトムアップ方式で考えている場合には、「下位階層から見て上位階層は論理的に整合的か」と考えていることになります。このときは、so what? が便利です。
so what? とは、日本語で言うところの「だから何?」です。
具体から抽象へ、あるいは、前提から結論へという流れになります。
上位階層と下位階層を比較して、一般性や抽象度が高いのは上位階層なのは変わりません。下位階層は具体的な命題や概念であり、そこから上位階層に抽象的な命題や概念を導きます。
具体的な事実や事例を示すだけでは、根拠を示せても、何が言いたいのかや何を主張したいのかがよく分かりません。そこで、下位階層の命題や概念に対して「だから何?」と尋ねられたとき、導ける結論やより高次の命題や概念を挙げて答えることになります。
図16.8.so what?
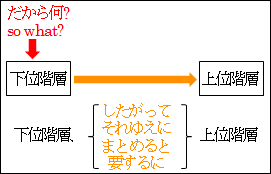
接続的な表現で言えば、「したがって」や「それゆえに」、「まとめると」や「要するに」といった表現で下位階層と上位階層が繋がるかを確認することになります。
5 注意点
続いて、論理ピラミッドを作るときの注意点に触れておきます。
まず、論理の繋がりの確率に気を付けなければなりません。
論理の繋がり、あるいは、因果関係の繋がりが長くなってくると、有り得るには有り得ることなのだが、現実問題としてその確率が非常に低くなって非現実的になることがあります。
この論理の繋がりの弱さを表すのに適した例に、諺である「風が吹けば桶屋が儲かる」を挙げることができます。
| (20.3)「風が吹けば桶屋が儲かる」という諺は、以下のような論理の繋がりになっている。この諺の論理の問題点を確率の観点から考えよ。 (1)(大)風が吹く ↓ (2)埃が舞い上がる ↓ (3)埃が目に入る ↓ (4)盲人が増える ↓ (5)盲人は三味線を買う ↓ (6)三味線には猫の皮が必要だから、猫が殺され数が減る ↓ (7)ネズミが増える ↓ (8)ネズミは桶をかじり、桶屋の需要が増える ↓ (9)桶屋が儲かる |
これは、「意外なところからに影響が出ることの喩え」、または、「当てにならない期待をすることの喩え」として使われる諺です。
一見すると「風が吹く」ことと「桶屋が儲かる」ことに繋がりがないように思えますが、
(1)(大)風が吹く
↓
(2)埃が舞い上がる
↓
(3)埃が目に入る
↓
(4)盲人が増える
↓
(5)盲人は三味線を買う
↓
(6)三味線には猫の皮が必要だから、猫が殺され数が減る
↓
(7)ネズミが増える
↓
(8)ネズミは桶をかじり、桶屋の需要が増える
↓
(9)桶屋が儲かる
という論理あるいは因果関係をたどって「風が吹く」ことと「桶屋が儲かる」ことを結び付けて、突拍子もない主張を作っています。
この諺は江戸時代にできたと言われています。
江戸時代ですら笑い話でしたから、いわんや現代をやです。
道はアスファルトで舗装され、医療も発達し、公衆衛生も改善され、材料も豊富にそろっている現代社会では、この一連の因果関係の繋がりは余計に認めがたいものに感じます。
過去の話を、現代の価値基準や状況から短絡的に一刀両断してしまうのは禁じ手なので、江戸時代に則って確率を考えてみましょう。ただし、この確率は適当で、しかも、多めに見積もります。
(1)「(大)風が吹く」ならば(2)「埃が舞い上がる」は、道がすべて石畳なわけでもないですし、確率的に90%くらいはありそうです。
(2)「埃が舞い上がる」ならば(3)「埃が目に入る」は、目を瞑るのが遅かったりして運悪く目に入ることもあるでしょうから、確率的に40%くらいとしましょう。
(3)「埃が目に入る」ならば(4)「盲人が増える」は、江戸時代でも埃が目に入って失明するというのは中々想像しにくいですが、医療も発達していないですし運が悪いと失明するかもしれないと一応認めましょう。20人に1人は、失明するかなと考えて、確率的に5%ととします。
(4)「盲人が増える」ならば(5)「盲人は三味線を買う」は、『平家物語』の「祇園精舎の鐘の声」の琵琶法師で有名なように、昔は盲人は三味線を弾きながら語り歩くことで、お金を得ていたので、商売道具の楽器三味線を買うことが多いでしょう。盲人の皆が皆三味線を買うわけではないですが、その数は多いでしょうから、確率的に70%ととします。
(5)「盲人は三味線を買う」ならば(6)「三味線には猫の皮が必要だから、猫が殺され数が減る」は、その通りでしょう。三味線を作るのに、猫の皮がいるので、三味線が売れれば、捕えられる猫の数も当然に増えます。確率的には、90%くらいあるのでしょうか。
(6)「三味線には猫の皮が必要だから、猫が殺され数が減る」ならば(7)「ネズミが増える」は、天敵の猫が減れば、ネズミの天下と言えそうです。ただちょっと安直な気もしますが、公衆衛生が悪く、ネズミが繁殖しやすかったことも踏まえて、確率的に30%とします。
(7)「ネズミが増える」ならば(8)「ネズミが桶をかじり、桶屋の需要が増える」は、ありそうですが、ネズミが桶をかじるのがどの程度のものなのか想像しにくいです。でも、桶は、ネズミにかじられ穴が空いてしまうと、使い物にならないので、買い替えようと考えるでしょう。確率的に60%とします。
(7)「ネズミは桶をかじり、桶屋の需要が増える」ならば(9)「桶屋が儲かる」は、その通りです。買い替えようと考えた人のほとんどが買うとします。確率的に80%とします。
さて、(1)~(9)までの因果関係の確率が順に90、40、5、70、90、30、60、80%となりました。と言うことは、(1)「風が吹く」ことから(9)「桶屋が儲かる」ことが起きる確率は、
| 0.9×0.4×0.05×0.7×0.9×0.3×0.6×0.8 =0.00163296≒約0.16% |
約0.16%。1%を余裕で切っています。625,000回に1回の確率です。
埃が舞い上がるほどの風が1日何回吹くかは定かではありませんが、625,000回それが起きてやっと1回起きる程度のことです。しかも、これは確率を多く見積もっての値です。
この確率を世間の人が聞けば、普通は、論理的な主張と言うには無理があると感じるのではないでしょうか。
| [解答] 論理の繋がり方が1つの命題から1つの命題を導くことを繰り返しているため、1つの1つの命題同士の繋がりがあることが妥当だとしても、全体で見たとき、最初の命題と最後の命題の繋がりが確率的に非常に低いものとなっている。 |
このように、1つの根拠だけを元にして結論を導く場合、その妥当性に注意を払う必要があります。
1つの上位命題と下位命題の繋がりの論理は十分に妥当であるのに、それが一本道でいくつも繋がって伸びて行くと、妥当性がどんどん薄まって行くことがあります。
たとえ、どの命題の繋がりも80%の確率だとしても、5個の因果関係で繋がると、0.85×100=約33%まで下がります。
もし10個の因果関係で繋がると、0.810×100=約11%まで下がってしまいます。
ですから、1つの根拠だけを元にして結論を導く場合、根拠と結論の間の繋がりの強さを十分に考えておき、安易につながないようにしておく必要があります。
ここで思い出してもらいたいのが、論理学の規則とその実践です。
まず、条件法「ならば(⇒)」の機能です。
「P ならば Q(P ⇒ Q)」といったとき、論理学の規則を厳密に守れば、「P であるとき、必ず Q である」ということになります。
「下位命題⇒上位命題」と表されるとき、確率的には100%です。
集合関係で言えば、下位命題は上位命題の部分になります。つまり、上位命題が下位命題を内包していることになります。
日常的な表現で言えば、「上位命題の典型的な事例は、下位命題である」、「上位命題の主たる根拠は、下位命題である」といったものになります。
また、上位命題が下位命題から100%の確率で導かれ、かつ、下位命題が上位命題から100%の確率で導かれる場合は、「P ⇔ Q」で表される関係もありました。
つまり、上位命題と下位命題が「同値」である関係です。
日常的な表現で言えば、「上位命題=下位命題」、「上位命題は下位命題と同等である」、「上位命題と下位命題は同意である」、「上位命題は下位命題と換言される」といったものです。
こうした論理学の⇒や⇔で命題が繋がっているのならば、どんなに階層が長くなっても、常に100%の確率で最下位命題から最上位命題まで繋がります。
しかし、論理学を厳密に守ると、現実の問題の分析をしたりするときに、不便が生じることになります。
日常の出来事は、常に100%の確率で起きるとは限りません。100%でないことの方が多いです。そうすると、論理学の⇒は使えなくなってしまいます。
ですから、論理的思考を実践するにあたって、確率的に十分高い場合や、そう考えることが妥当であると言える場合には、条件法「ならば」を使えるように、論理学の規則を緩めました。
規則を緩めたからには、その弊害も当然出てきます。論理学が持つ推論の正しさが損なわれます。
実際、論理学では「P ⇒ Q」としたら、100%そうなるはずなのに、論理的思考の「論理」では確率的な話が入ってきてしまっているわけです。
このように、論理学の規則を緩めたために、生じている弊害を忘れてはいけません。
1組の上位命題と下位命題の関係ならば、論理的思考における緩めた規則でも妥当であり、大した問題もなく、許容されることも多いでしょう。
しかし、部分的な1組の上位階層と下位階層の命題同士の繋がりの確率の高さに目を奪われて、全体で見たときの確率、因果関係の繋がりの弱さを考慮していないと、現実離れした無茶な主張になり得ることに気を付けてください。
その対策としては、常に最下位命題から最上位命題に繋がる論理の妥当性があるのかを意識しておくことから始めます。
まず、無闇に階層を増やし過ぎないように気を付けることが大切です。
論理の繋がりがどんなに強くても、繋がりが長くなると、次第に繋がりが弱くなっていく傾向があります。特に、主張の重要な部分では、階層を減らすように努めるべきです。
どうしても、論理の繋がりが長くなって階層が増えてしまう場合は、繋がりが妥当なのかの検査をいつも以上に入念にしておくことが必要です。
次の対策は、命題の表現をより適切なものにすることを意識することです。
「風が吹けば桶屋が儲かる」という諺は、「風が吹くならば桶屋が儲かる」ということを言っているので、説得力のないものになっています。そこで、「風が吹くならば、桶屋が儲かることが非常に珍しいことだが有り得る」という表現にすれば、この主張に意味や価値があるのかどうかは置いておくとしても、論理的には一応許容されるようになります。
このように、命題に「~の可能性がある」や「~ということもあり得る」といった表現を加えることで、確率を反映したものにする方法があります。
ただし、こうした表現を用いると、断定するよりも不確実な主張であることを認めていることになります。
そうすると、説得力が落ちるため、相手から不確実性を指摘され、突っ込まれることが多くなります。いつでも断定できるわけではないので、こうした表現を使わざるを得ない場合があるのは確かですが、できるだけこうした表現を多用するのは避けるべきです。
こうした表現を避けるためにも、断定的な表現にできるように、事実に基づいた確実な推論を積み重ねることが大切になります。
そして、一本道の論理の繋がりにしないことも対策となります。つまり、根拠となる前提である下位命題を1つではなく2つ以上にして、上位命題を導くようにする方法です。
上位命題と下位命題が1対1になっていると、「下位命題のとき、必ず上位命題である」ということになるのが基本でした。
そこで、下位命題を新たにもう1つ追加して、「下位命題1 ⇒ 上位命題」かつ「下位命題2 ⇒ 上位命題」とすれば、より説得的な主張になります。
例えば、「風が吹けば、桶屋が儲かる」の特に確率が低かった箇所の、(3)「埃が目に入る」ならば(4)「盲人が増える」を考えてみましょう。
(3)「埃が目に入る」ならば(4)「盲人が増える」は、下位命題が1つで上位命題が1つなので、1対1になっています。
今ここで、下位命題に(3')「埃が網膜を傷つける」を新しく追加してみます。
| (3)埃が目に入る かつ (3')埃が網膜を傷つける ⇒(4)盲人が増える |
そうすると、(3)「埃が目に入る」ならば(4)「盲人が増える」、かつ、(3')「埃が網膜を傷つける」ならば(4)「盲人が増える」となります。
したがって、(3)「埃が目に入る」かつ(3')「埃が網膜を傷つける」ならば(4)「盲人が増える」となります。
つまり、単に(3)「埃が目に入る」だけではなく、同時に(3')「埃が網膜を傷つける」ことがあるとき、必ず(4)「盲人が増える」ことになります。
もし(3)「埃に目が入る」ことが偽、つまり、発生しなければ、当然(4)「盲人が増える」ことは起きません。
また、(3)「埃に目が入る」ことが真であり、発生したとしても、(3')「埃が網膜を傷つける」ことが偽で発生しなければ、(4)「盲人が増える」ことは起きません。
新たな下位命題(3')「埃が網膜を傷つける」が加わることによって、論理の繋がりが一本道ではなくなったために、適切な論理の繋がりだと思えます。
なお、勝手に新しい条件や根拠を加えているため、これでは「風が吹けば桶屋が儲かる」という諺の言いたいことを殺してしまうことにもなります。が、しかし、この諺は、元々論理的思考で検討すると無理のある主張なので、仕方のないことです。
このように、前提となる下位命題が増えることで、結論たる上位命題が成立する条件が厳しく狭くなるということが起きます。
したがって、複数の下位命題によって上位命題が導かれる確率が高くなります。つまり、論理や因果関係の繋がりが、強化されます。
論理の繋がりが一本道になる場合は、本当に下位命題と上位命題の繋がりが一本だけで良いのか、見落としている下位命題はないか、もっと条件や根拠となる下位命題がある方が適切ではないのか、ということを考えてみてください。
以上のように、論理ピラミッドを作る際には、上位階層と下位階層の繋がりが適切かをよく考える必要があります。
| 論理ピラミッド作成の注意点 論理ピラミッドが大きくなったとき論理の繋がりが弱くなりやすい
|
6 まとめ
以上、論理ピラミッドの基本的な特徴と作り方についての解説が終わりました。
論理ピラミッドを用いると、論理的な主張を構築したり、整理したりすることに役立ちつことが分かりました。
論理ピラミッドについてまとめておきましょう。
論理ピラミッドの作り方
論理ピラミッドの特徴
論理ピラミッド作成の注意点 論理ピラミッドが大きくなったとき論理の繋がりが弱くなりやすい
|

論理ピラミッドは、目的達成志向で客観的な事実や事柄をグル―ピングして、抽象化して上位命題を作成していきます。
各命題は、主語と述語で書き表すのが基本となります。
そして、論理ピラミッドを実際に作る段階になると、具体的な命題から抽象的な命題へという流れの下に、下位階層から抽象化していく、ボトムアップ方式・積み上げ方式による総合・統一が主になります。
しかし、トップダウン方式・逆算方式もあり、一般的・抽象的な結論から、個別的・具体的な根拠たる前提へという流れで考える場合もあります。
実際に論理ピラミッドを作るときには、トップダウン方式やボトムアップ方式は、どちらか一方のみしか使わないというわけではなく、部分的に両方とも用いられることも普通にあります。
これが論理ピラミッドの基本的な特徴と作り方です。
これを踏まえて、続いて、論理ピラミッドを用いて、「現象型」の問題を分析する方法を見て行きます。
そして、その後は、論理的な文章作成や読解、発表において、論理ピラミッドをどのように利用するかについて触れたいと思います。
前頁:第19章 因果関係図
ページトップへ:第20章 論理ピラミッドの基本
次頁:第21章 論理ピラミッド -現象型の問題 -