前頁 |▼| 次頁
第10章 論理的思考のまとめ
論理的思考のために論理学の基礎と、それを拡張した演繹法、狭義の帰納法、仮説推論、類比推論、観念連合、弁証法を学んできました。
そこで、今まで学んできたことを一度まとめなおして整理します。
論理的思考を体系化することが目標です。
加えて、類似と対比の考え方と、因果関係と相関関係の考え方を学びます。
| 目次 |
| 1 講義の総括 2 講義の整理 3 類似・対比 4 因果関係と相関関係 テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 講義の総括
今まで論理的思考がどういったものかを学んできました。
第1章では、論理的な主張に必要な要素として、結論と根拠を挙げて、それが論理的であるためには関連性が必要であることを説明しました。
第2章では、正しく推論するための基礎中の基礎として、論理学の観点から前提命題と結論命題、肯定と否定、全称と特称、連言と選言、条件法があることを説明しました。
第3章では、三段論法による基本的な正しい推論の形式を、定言、選言、仮言の3種類に分けて説明しました。
第4章では、三段論法の延長上に演繹法を説明しました。演繹法は一般的・普遍的・抽象的な法則や命題から、個別的・特殊的・具体的な命題を推論するものでした。
第5章では、演繹法と反対である個別から一般への推論である帰納法を説明しました。そこでは正しい推論が正しい結論を導くとは限らないことに注意が必要でした。
第6章では、帰納法に関連して、仮説推論について説明しました。論理的であるためにも、仮説形成だけでなく、仮説検証を行うことが重要でした。
第7章では、さらに帰納法に関連して、類比推論について説明しました。事物の類似性に注目した推論でした。これも検証が重要になってくる推論でした。
第8章では、帰納法のまとめとして、観念連合という考え方について学びました。私達の思考が経験に基づくことを確かめました。
第9章では、弁証法に基づいた統一的理解について説明しました。推論と呼ぶにはかなり乱暴ではあるが、発想の第一歩として非常に有益であることが分かりました。
論理的思考の推論方法に関連して、様々な用語も解説してきました。
第4章では、対となる概念として、一般と個別、普遍と特殊、抽象と具体、これらに加えて相対的と絶対的について学びました。そして、代表して抽象化と具体化を詳しく見ました。
第6章では、定説、通説、多数説、有力説、少数説等、仮説の支持され方に応じて種類があることを学びました。
第7章では、類比推論の言語的な応用として比喩について詳しく見ました。
第8章では、観念・概念・範疇について詳しく見ました。おまけとして表象・形象・心象についても解説しておきました。
第9章では、論理的思考を端的にかつ統一的に理解するために、分析・総合・直観の関係を説明しました。
2 講義の整理
推論方法を整理するために、範疇・カテゴリーに応じて各推論方法を分類していきましょう。範疇の分類は、ある基準の下に概念を振り分けて分類していくことになります。このとき、「A である」か「A ではない」が役に立ちます。
まず、正しい推論を行えば結論が必ず正しくなるかどうか、という基準がありました。これによって、演繹法と広義の帰納法に分けられます。
図10.1.推論のまとめ 画像クリックで拡大 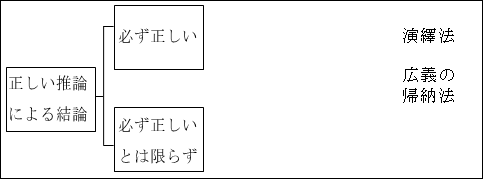
そして、広義の帰納法の中で、さらに分類されます。正しい推論だとしても、必ずしも正しい結論になるとは限らない、という共通点がある中で、各推論によって特徴がそれぞれありました。正しい結論 とは限らないという点からは、すべての帰納法は仮説性のあるものになります。つまり、事象が生じる理由についての合理的な説明で有り得るというものにとどまるということです。
その中で、仮説性が強いモノと弱いモノがありました。仮説性が強いとは、仮説である度合いが強いことですが、他の推論以上に検証をしっかりと行わなければなりません。仮説性が弱ければ、仮説であるとは言え、観たままをそのまま説明しているので、検証も簡単に行えたりします。
複数の個別的・特殊的・具体的前提から、一般的・普遍的・抽象的結論を導くという帰納法の典型的な形式である枚挙的帰納法、つまり、狭義の帰納法は、観察したものを合せただけなので、仮説性が弱かったです。もちろん、結論に反する事例が観察されれば、結論は修正されることになりますが、基本的に観察された事実にのみに基づいているので、仮説性は弱いです。それ以外の帰納法の結論は、思い付き的な発想や、直観的な発想等の面が強く仮説性が強くなりました。
図10.1.推論のまとめ 画像クリックで拡大 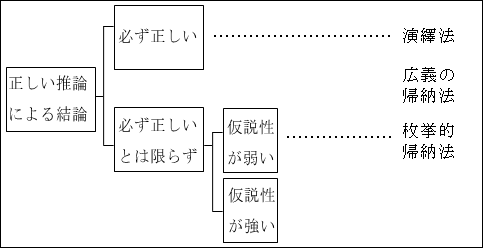
帰納法の中で、さらに仮説性が強いものは、仮説推論となります。ただし、仮説推論の中でも、特に類似性に注目して推論する場合は、類比推論と言われました。
図10.1.推論のまとめ 画像クリックで拡大 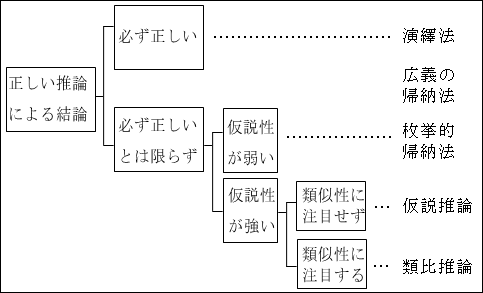
そして、演繹法でも帰納法でもないものに弁証法がありました。しかし、この講義では、推論の結論が正しいとは限らないという点を以って、広義の帰納法に大雑把に分類することにしていました。統一的理解を目指す弁証法も仮説性が強かったです。
図10.1.推論のまとめ 画像クリックで拡大 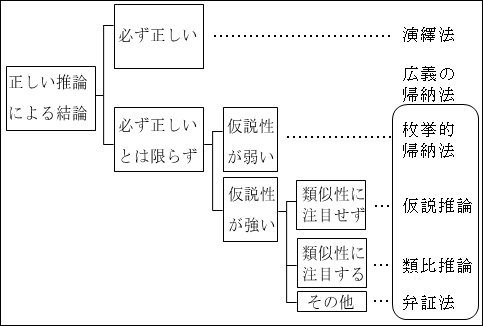
推論の前後における情報量に関して言えば、変わらないか増えるかで演繹法と広義の帰納法とに分けられます。推論後でも情報量が変わらなければ、演繹法です。推論後に情報量が増えれば、広義の帰納法となります。
なお、情報量が変わると必ず増える理由は、推論によって減ることはないからです。減ることがなく変わるのだから、増えるに絞られるわけです。なぜならば、数量の増減とは、「減少・不変・増大」の3種類ですが、「変わる」としたら、「減少・増大」のみになりますが、さらない「減ることはない」という条件が加わっているので、必然的に「増大」のみが残ることになります。
| 数量の増減 減少 ↓変わる=不変を否定 ↓減らない=減少を否定 増大 |
このように正しく推論の形式に則って、根拠たる前提が結論を支えることが、論理的であるために重要でした。
第1章 論理的であるとは
| 論理的であること =正しい推論+正しい知識 (1)形式面 論理的主張 || 結論 (2)内容面 + ← 関連性 根拠 + 隠れた前提の発見 |
各推論方法に則ることが形式面の論理性を支えることになります。各推論の典型的な型を図示すると次のようになりました。
図4.3.演繹法の論理構造
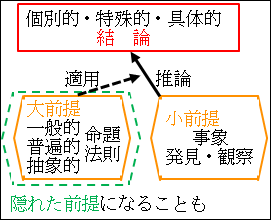
図5.3.帰納法の論理構造
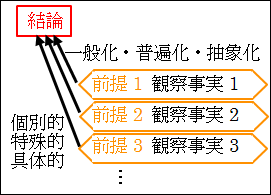
図6.2.仮説推論の構造
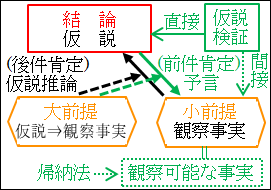
図7.1.類比推論の構造
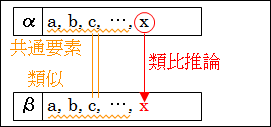
図9.1.弁証法
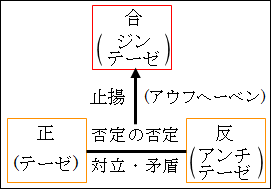
という論理構造になっています。
この形式面の論理性に加えて、内容面から論理性を支えるためには、各命題や事実の中に関連性を見出すことが重要でした。また、論理的に飛躍を感じる場合などは、隠れた前提がある場合が多多かったです。これは形式面と内容面から推測することになります。自分が話している場合は、相手との共有されている認識や知識を探りながら、隠れた前提として明示せずに簡潔に話を進めるかどうかを決めなければなりませんでした。
内容面の論理性を支える関連性を見つけるときには、対象をよく観察する必要があります。
よく観察することを具体的に言うと、対象を分析することが必要です。対象を部分へと分解して明らかにすることで、その構成要素と特徴が理解できます。様々な対象を分析することで、対象の関連性を見つけ出すことができます。分析の結果、関連性が見つけることができれば、それを推論形式に当てはめる等、総合していくことで、論理を構築していくことができます。
また、分析と総合を実行するときには、抽象化と具体化の能力も重要になります。
図4.1.抽象化と具体化
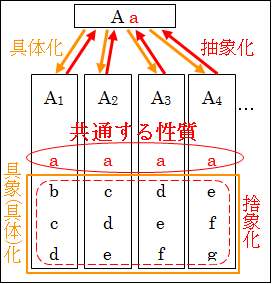
分析していき関連性が分かると、抽象化して一般的・普遍的・抽象的な概念や命題を総合的に構築する。
逆に抽象的な概念を理解するために、何かしらの関連性を手掛かりに、個別的・特殊的・具体的な概念や命題を具体化して分析していく。
図9.4.分析と総合と直観
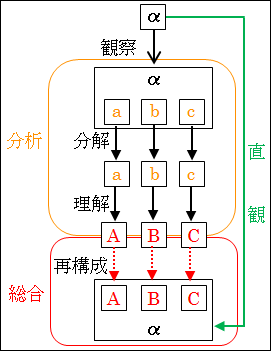
このように、抽象化と具体化は総合と分析にも密接に関わっていることが分かります。
対象の関連性を見出すことに関係して、類似、対比、因果の3つの関係について説明しておきたいと思います。これは、対象の関連性は大きく分けて、類似、対比、因果の3つの関係を見出すことができるためです。
関連性とは、2つの対象の相互の関係性を見つけ出すことにつながります。なぜ2つの対象かと言えば、人間の意識の働きがそのようになっているからです。これは観念連合が関係してきます。観念連合とは、ある対象を知覚したときに、別の観念と結びつくことでした。要するに、対象を分析するとき、2つの観念、つまり、対象についての2つの意識が結びついていることになります。
それでは、2つの観念がどのように結びついて思考することを、類似、対比、因果の3つに関連させながら、見てみることにします。
3 類似・対比
まず対象を分析すると、似ている点が分かります。似ている点は、類比推論に代表されるように、様々な推論を導いていく際に、類似点に注目しているコトが分かるはずです。また、抽象化でも共通要素という類似点を抽出していました。具体化でも、抽象的概念を共通要素を持つ具体的な概念へと導いていました。このように論理的思考では、何かと何かが似ていること、つまり、類似に気付くことが第一歩です。
類似とは、ある対象が、別の対象と同じ要素、または似ている要素をもつことです。英語では、similarity と言います。類義語には、相同、類比、相似等があります。
対象 α と β を分析したとき、α には要素 a、b、c、k があることに気付き、β には要素 a、b、c、l があることに気付きます。
図10.2.類似と対比 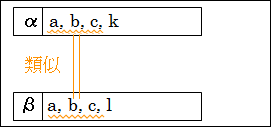
そうすると、α と β は、a、b、c という要素を持っている点で類似していることが分かります。
そして、対象同士が似ていることに気付くと、似ていない点、つまり、異なる点にも気付くことになります。
対比とは、ある対象が、別の対象と異なる要素、または対立する要素をもつことです。英語では、contrast と言います。類義語には、相違、対照等があります。そして、対比は類似の対義語と言えます。
先程の対象 α と β で言えば、類似点として要素 a、b、c がありました。しかし、α の要素 k と、β の要素 l は異なります。
図10.2.類似と対比 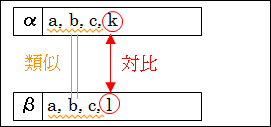
ここに注目すると、α は、要素 k を持っているという点で、β とは異なると言えます。
逆に、α は、要素 l を持たないという点で、β とは異なると言えます。
さらには、α と β は、要素 k と l という点で異なるとも言えます。
このように、対比は、2つの対象が異なる特徴に注目して比べることで、対象の特徴をより鮮明にすることができます。
ただし、対比で注意しなければならないコトは、全く関係のないものは対比しても意味が無いことが多いです。
例えば、犬についてペットとしての本質を掴もうしているとします。ただ犬だけを考えていても中々分からないので、比較対象を持ってきます。
このとき、比較対象として猫を選ぶのは有効です。哺乳類で四足歩行で、大きさも似ており、ペットとしては同じ位人気の猫と犬を対比すれば、似ている点が多い分、犬と猫に違いがあればそれが鮮明になるからです。
しかし、鉛筆と対比した場合はどうでしょうか。鉛筆はペットどころか生き物ですらありません。共通点や類似点もありません。これでは対比しようにも対比できません。無理に対比しても分かるのは、犬と鉛筆はまったく異なるということばかりです。
このように、対比するときとには、何かしら類似点があることが必要になります。類似しているからこそ相違が浮かび上がり対比できると言えます。弁証法を思い出して欲しいのですが、正・テーゼと反・アンチテーゼは、相互に対立・矛盾する関係にありました。しかし、正と反は、互いに共通する要素があるからこそ、相互に結びつき対立・矛盾関係に陥っていました。このように、対比は、何かしらの類似点、共通要素があるからこそ浮かび上がるもだと分かります。
余談ですが、このように、無関係のものを比較することは、だいたい徒労に終わりますが、誰も気付かなかった類似や対比を見つけ出せれば、大発明や大発見につながることもあります。無駄である可能性が高いことを踏まえつつも、あえて比較してみると面白いかもしれません。
4 因果関係と相関関係
類似と対比は2つの対象を比較することで、その特徴を明らかにして関連性を見出すものでした。因果関係は、これと少し毛色が異なります。
因果関係は英語で、the relation of cause and effect と言います。cause が原因で、effect が結果です。因果のみに絞って言えば、causality と言います。
これからも分かるように、因果関係は、その名の通り、原因と結果の関係です。これは、2つの対象 C と E において、原因 C が、結果 E を引き起こすことを意味します。言い換えると、結果 E は、C が原因となって生じるということになります。
| 原因 C ⇒ 結果 E |
例えば、(10.1)の例を見てください。
| (10.1)次の前提から何が分かるか <前提1> 同じ環境のネズミの集団がいる <前提2> その集団を、発ガン性物質を投与したネズミの集団と何もしないネズミの集団に分ける <前提3> 発ガン性物質を投与したネズミの集団はガン発症率が高い <前提4> 何もしないネズミの集団はガン発症率が低い [結論] |
ネズミを使った発ガン原因についての実験を考えます。
まず、同じ環境で飼育したネズミの集団を用意します。同じエサや同じ気温、同じ運動量などすべての要素を同じにするということです。
その集団の中で、発ガン性物質を投与するネズミの集団と、何もしないネズミの集団に分けます。
そして、発ガン性物質を投与したネズミの集団では、ガンを発症するネズミが多く現れたのに対して、何もしないネズミの集団ではガンの発症率が変わらないという結果になったとします。
前提1と前提2から、2つのネズミの集団は、同じ環境で育っているため、「すべて同じ条件で育ったていると言えるが、発ガン性物質を投与するか否かの違いがある」ことが分かります。
| (10.1.1) <前提1> 同じ環境のネズミの集団がいる <前提2> その集団を、発ガン性物質を投与したネズミの集団と何もしないネズミの集団に分ける [結論1] ネズミはすべて同じ条件だが、発ガン性物質の投与があるか否かの違いがある |
前提3と前提4から、「発ガン性物質を投与したネズミの集団は発ガン率が高くなったのに、何もしていないネズミの集団は発ガン率が変わらない」ことが分かります。
| (10.1.2) <前提3> 発ガン性物質を投与したネズミの集団はガン発症率が高い <前提4> 何もしないネズミの集団はガン発症率が低い [結論2] 発ガン性物質を投与したネズミの集団は発ガン率が高くなるが、何もしていないネズミの集団の発ガン率は変わらない |
結論1と結論2を新たな2つの前提として考えると、「発ガン性物質はガンの発症率を高める」、つまり、「発ガン性物質を原因として、ガンの発症という結果を引き起こす」という因果関係があることが分かりました。
| (10.1.3) <結論1=前提> ネズミはすべて同じ条件だが、発ガン性物質の投与があるか否かの違いがある <結論2=前提> 発ガン性物質を投与したネズミの集団は発ガン率が高くなるが、何もしていないネズミの集団の発ガン率は変わらない [結論] 発ガン性物質は、ガンの発症率を高める = 発ガン性物質は、ガンの発症の原因である |
| (10.1)次の前提から何が分かるか <前提1> 同じ環境のネズミの集団がいる <前提2> その集団を、発ガン性物質を投与したネズミの集団と何もしないネズミの集団に分ける <前提3> 発ガン性物質を投与したネズミの集団はガン発症率が高い <前提4> 何もしないネズミの集団はガン発症率が低い [結論] 発ガン性物質は、ガンの発症の原因である |
今の説明を簡潔にすると、次のように表せます。
| (10.1.4) 発ガン性物質を投与する ⇒ ガンを発症する 発ガン性物質を投与しない ⇒ ガンを発症しない ただし、その他の条件はすべて同じ ∴原因は、発ガン性物質 |
なお、このように、1つのみを変えて他のすべてを同じにして比較する実験を対照実験と言います。
英語では、scientific control と言います。条件を1つだけ変える理由は、条件を2つ以上変えると、どの条件が原因となって異なる結果が引き起こされているか特定できないからです。つまり、対照実験は、結果を引き起こす原因を特定するための実験と言えます。
先のネズミの実験で言えば、発ガン性物質を投与する以外にも、不摂生な食事と健康な食事と違いをつけていたとします。
| (10.1.5) 発ガン性物質の投与、かつ、不摂生の食事 ⇒ ガンを発症する 発ガン性物質の不投与、かつ、健康な食事 ⇒ ガンを発症しない 原因は、発ガン性物質か、不摂生の食事か? |
そうすると、発ガン率が高いという結果が出てもその原因が、発がん性物質によるものなか、食事の違いによるものなのか、分からなくなります。
もっと身近な例で言えば、懐中電灯が点かなくなったとします。
| (10.2)懐中電灯が点かない原因の探求 |
この懐中電灯が点かない状態のものを A とします。
そこで、電池を入れ換えてみます。これは、「電池が切れている」ことが原因と予想しています。そして、電池を入れ換えてみたら、懐中電灯が点いたとします。このことから、懐中電灯が点かなくなった結果を引き起こした原因は、「電池切れ」だと分かりました。
| (10.2.1) 電池交換せず ⇒ 電灯点かず 電池交換 ⇒ 電灯点く ∴原因は、電池切れ |
ここで、仮に電池交換しても懐中電灯が点かなかったとします。
次に、電球を入れ換えてみます。これは、「電球が切れている」ことが原因と予想しています。ただし、電池は、最初の状態 A の元の電池に戻しておきます。そして、電球を入れ換えてみたら、懐中電灯が点いたとします。このことから、懐中電灯が点かなくなった結果を引き起こした原因は、「電球切れ」だと分かりました。
| (10.2.2) 電球交換せず ⇒ 電灯点かず 電球交換 ⇒ 電灯点く ∴原因は、電球切れ |
もし電池を状態 A の元の電池に戻さずに電球を交換したとすると、電池交換と電球交換を同時に行ったことになります。そして、この場合に、懐中電灯が再び点いたとします。
| (10.2.3) 電池交換せず、かつ、電球交換せず ⇒ 電灯点かず 電池交換、かつ、電球交換 ⇒ 電灯点く 原因は、電池切れか、電球切れか? |
そうすると、「電池切れ」か、または、「電球切れ」かのどちらかが原因であることは分かりますが、どちらが原因なのかは特定できません。もしかしたら両方が原因かもしれません。このように、条件を1つのみ変える対照実験は、原因を特定するためには必要な実験だということが理解できます。
対照実験が、因果関係の特定に効果的なのことに納得できた所で、対照実験の現実的な問題点を指摘しておきたいと思います。
実際問題として、現代の複雑な社会や複雑な自然現象では、因果関係があると言うことは非常に困難です。懐中電灯の例からも分かる通り、原因と疑われる要素は多数あります。複雑な問題を扱うとき、その複雑さ故に、その1つの条件だけを変えて実験することが難しいです。
特に、社会制度等に関する実験は、一般の人の生活に大きく関わってくるために、おいそれとできません。因果関係が知りたいから赤ん坊を集めて一から実験に適するような環境で育てるなど人権上許されません。したがって、因果関係を特定するのは非常に困難なわけです。そして、実験の条件を揃えて行うことの困難さは、因果関係があるか否かまで言えないことにまでつながる場合もあります。
よく言われる例として、(10.3)「動物を飼ている人は心優しい人である」という言説です。
| (10.3)次の命題の主語を条件として条件法になおし、その真・偽を判定せよ 動物を飼っている人は心優しい人である |
これは、「S は M である」という定言の形式をしていますが、「P ならば Q である」という条件の形式に直せます。
| (10.3)次の命題の主語を条件として条件法になおし、その真・偽を判定せよ 動物を飼っている人は心優しい人である 動物を飼っている人ならば、心優しい人である |
「動物を飼っている人ならば、心優しい人である」という命題は、因果関係を表しているように読めます。つまり、「動物を飼っている」ことが原因として、「心優しい」が結果となります。
確かに、「動物を飼っている人は心優しい人である」場合が多い気がします。何となく正しそうに感じます。実際、「動物を飼っている人は心優しい」という統計調査もあります。でも本当に、「動物を飼うこと」は、「心優しい」ことの原因と言えるのでしょうか。つまり、因果関係があると言ってもいいのかという疑問です。
なぜならば、「心優しい」ことの原因の候補が、「動物を飼う」こと以外にも簡単に想像できて、かつ、多くあり過ぎます。さらに、対照実験を行うことは事実上不可能です。つまり、ちょっと考えれば、多様な生活環境や人生経験の中で、「動物を飼っている」か否かの条件のみが異なる人を比較する実験を行うことは、事実上不可能だということがすぐに分かります。
このような条件の下で、「動物を飼う」ことが「心優しい」ことの原因と本当に言えるのでしょうか。もし因果関係があると言えると仮定するならば、ネズミの実験、懐中電灯の実験の例に則れば、このように言えるはずです。
| (10.3.1)対照実験の成否 動物を飼わず ⇒ 心優しくない 動物を飼う ⇒ 心優しい その他の条件はすべて同じ |
しかし、現実には、その他の条件はすべて同じではありません。
| (10.3.1)対照実験の成否 動物を飼わず ⇒ 心優しくない 動物を飼う ⇒ 心優しい その他の条件はすべて同じではない |
したがって、動物を飼うか否かで集団を分けて調査しても、その他の条件を同じにそろえて調査できていないので、対照実験としては不完全となります。
実際、
動物を飼っていなくても、心優しい人はたくさん居ます。例えば、私がそうです。
反対に、動物を飼っていても、心優しくない人もたくさん居ます。例えば、私の友人がそうです。猫を飼っていますが、性格は傲慢で人を見下すし、他人への態度が悪いです。いわゆるクズです。
こう考えると、「動物を飼う」かどうかは、「心優しい人である」ことには、原因と結果の関係は簡単には見出せないような気がしてきます。このことから、命題「動物を飼っている人ならば、心優しい人である」は偽と言えるんじゃないかと思えてきました。
しかし、統計調査では、「動物を飼っている人は心優しい人」が多いことが言われています。要するに、動物を飼っていない場合よりも、飼っている人の方が心優しいという確率が明らかに高い、という統計があることを意味しています。そういう調査が行われて本当に存在するならば、これは認めるしかありません。そこで、これをどう考えるかが問題になります。
対照実験のように条件が1つだけ異なるとは言えない中で、因果関係を探るには、まず相関関係があるか確かめることになります。
相関関係とは、2つの対象が相互に関連して変化・発生する関係です。つまり、2つの対象 X と Y があり、X が変化・発生するとき、Y も変化・発生する場合のことです。ちなみに、英語では、correlation と言います。
相関関係と因果関係の区別は重要です。
因果関係では、原因 C が結果 E を引き起こすという 原因 C ⇒ 結果 E が明確でした。
しかし、相関関係では、X ⇒ Y とは限りません。単純に X と Y が同時に発生したり変化・発生するという関係にあるだけです。X が Y を引き起こしているかもしれませんし、Y が X を引き起こしているかもしれません。X と Y のどちらが原因でどちらが結果なのかは分かりません。分かっていることは、同時に変化・発生していることのみです。
| 因果関係 原因 C ⇒ 結果 E 相関関係 対象 X が変化・発生 かつ 対象 Y が変化・発生 X ⇒ Y、Y ⇒ X のどちらかは不明 |
もっと詳しく言えば、相関関係は、
対象 X が変化するとき、同時に対象 Y も変化するということは、対象 X が変化しないときには、同時に対象 Y も変化しない、
対象 X が発生するとき、同時に対象 Y も発生するということは、対象 X が発生しないときには、同時に対象 Y も発生しない、
ということが観察されることになります。
こうなる理由は、
対象 X が変化・発生しているときに、対象 Y が変化・発生していないとすると、対象 X と対象 Y が相互に関連して変化・発生していない、
対象 X が変化・発生していないときに、対象 Y が変化・発生しているとすると、対象 X と対象 Y が相互に関連して変化・発生していない、
ということになるからです。これでは、対象 X と対象 Y は別々に変化・発生していることになり、相関関係がないことになります。
したがって、「動物を飼う人は心優しい人である」という統計調査の結果は、因果関係まで示しているかは分からずとも、少なくとも相関関係があることを示していることになります。
つまり、「動物を飼う」ことと「心優しい」ことの両方が観察されていることになります。
そして、「動物を飼っていない」ことと「心優しくない」ことの両方も同時に観察されていることになります。
| (10.3.2)相関関係の発見 動物を飼う かつ 心優しい 動物を飼わず かつ 心優しくない |
この結果が統計調査で得られたことになります。
再度注意を促しますが、ここに相関関係を見出すことはできても、因果関係までは見出せていません。
因果関係ならば、原因 C ⇒ 結果 E という原因・結果の関係の構造があることになりますが、
相関関係では、X ⇒ Y なのか、Y ⇒ X なのか、までは分からず、単純に、X と Y が同時に変化・発生することとが分かるだけだからです。
統計だけでは、相関関係の有無は確認できますが、因果関係までは分かりません。
そこで、因果関係を見つけ出すためには、相関関係を前提として、どちらが原因でどちらが結果なのかを特定しなければなりません。しかしながら、「動物を飼う人は心優しい人である」というのはどちらが原因で、どちらが結果なのか特定するのは非常に難しいです。
確かに、「動物を飼う」ことが原因として、「心優しい」ことが結果になっても良さそうです。つまり、「動物を飼う」ことで、「心優しく」なると考えても良さそうだ、ということです。これならば、「動物を飼う ⇒ 心優しい」という因果関係があると言えることになります。
しかし、「心優しい」ことが原因として、「動物を飼う」という結果になっても良さそうです。つまり、「心優しい人」だから、「動物を飼う」と考えても良さそうだ、ということです。この場合、「心優しい ⇒ 動物を飼う」という因果関係になります。原因と結果が入れ替わってしまいます。
| (10.3.3)因果関係の特定 動物を飼う ⇒ 心優しい 心優しい ⇒ 動物を飼う |
そして、この2つ因果関係のどちらが正しいのかは、人によって生い立ちや環境が複雑過ぎて分かりません。したがって、「動物を飼う人は心優しい人である」という考えは、因果関係ではなく、相関関係があるとまでしか言えないことになります。
このことから、(10.4)「動物を飼う人は心優しい人なのだから、君も動物を飼えば、心優しくなれるよ」といった主張は、論理的に弱点を抱えたものになります。
| (10.4)(10.3)を利用して、次の主張を仮言三段論法に直し問題点を指摘せよ 動物を飼う人は心優しい人なのだから、君も動物を飼えば、心優しくなれるよ |
これは「動物を飼う人ならば、心優しい人である」が大前提、「君も動物を飼う」が小前提になり、「心優しくなれる」が結論となる仮言三段論法の前件肯定規則です。
| (10.4)(10.3)を利用して、次の主張を仮言三段論法に直し問題点を指摘せよ 動物を飼う人は心優しい人なのだから、君も動物を飼えば、心優しくなれるよ <大前提> 動物を飼う人は心優しい人である → 動物を飼う人ならば、心優しい人である <小前提> 君も動物を飼う [結論] 君は心優しくなる |
仮言三段論法の前件肯定規則に当てはまるので、これは推論の形式は正しいです。しかし、大前提の内容面の正しさが問題になります。
「動物を飼う ⇒ 心優しい」という因果関係が明確にあるのなら正しいと言えますが、(10.3)で見た様に、大前提「動物を飼う人ならば、心優しい人である」は真とまでは言えないので、内容面から正しくありません。したがって、結論「心優しくなれる」が正しいとは限らなくなります。
このように、相関関係があることを、因果関係と捉えると誤った推論になる確率が高いです。
仮に「心優しい ⇒ 動物を飼う」であった場合はどうでしょうか。
| (10.4.1) <大前提> 動物を飼う人は心優しい人である → 心優しい人ならば、動物をかっている <小前提> 君も動物を飼う [結論] 君は心優しくなる |
「心優しい ⇒ 動物を飼う」という因果関係だった場合、小前提「動物を飼う」ことは三段論法の後件肯定なので、必ずしも正しい結論を導くとは限りません。
いずれにしろ、正しく主張するために、因果関係があると誤解されないようにしておく方が無難です。
| (10.4.2)相関関係を意識した主張 動物を飼うことと心優しいことには相関関係がある。 したがって、心優しい人が動物を飼っているだけかもしれないが、君も動物を飼えば心優しくなるかもしれない |
「動物を飼うことと心優しいことには相関関係がある。したがって、心優しい人が動物を飼っているだけかもしれないが、君も動物を飼えば心優しくなるかもしれない」と抑え目に表現しておくべきです。
こうした、相関関係があることしか分かっていないのに、まるで因果関係があるかのように主張する人は、日常生活でも見かけることが少なくないです。これは、論理的思考では誤りです。しかも、論理的思考の仮面を被っているだけに、騙されてしまうことも多いです。それ故に、因果関係と相関関係をハッキリと区別しておかなければなりません。「~だから…」「~ゆえに…」と言う場合、本当に因果関係があるのか疑う癖をつけておきましょう。
因果関係と相関関係の区別の重要性が理解できたところで、相関関係があるように見えても、偶々、相関関係があるように見えているだけの可能性もあることに注意が必要です。
これを擬似相関と言います。つまり、実際には別の要因によって引き起こされているが、2つの対象に相関関係があるように見えているだけの関係です。擬似とは、本物によく似ており紛らわらしいコトを意味しますが、「擬似相関」と言うと、「相関関係」に「よく似ているが違うコト」を意味しています。
相関関係では、2つの対象 X と Y が同時に変化・発生しているのが観察されていることでした。しかし、擬似相関では、実は、もう1つの対象 Z が、2つの対象 X と Y を引き起こしているだけで、X と Y には相互に関係がないことになります。
| 因果関係 原因 C ⇒ 結果 E 相関関係 対象 X が変化・発生 かつ 対象 Y が変化・発生 X ⇒ Y、Y ⇒ X のどちらかは不明 擬似相関 対象 Z によって、2つの対象 X と Y が発生・変化する X と Y は関係ない |
この擬似相関の例でよく使われる例が、(10.3)「アイスクリームの売上が増えると、水難事故が増える」というものです。
| (10.5)次の命題に因果関係または相関関係はあるか アイスクリームの売上が増えると、水難事故が増える |
「アイスクリームの売上が増えると、水難事故が増える」というコトからは、「アイスクリームの売上の増加」と「水難事故の増加」に相関関係があるコトが分かります。早まって考える人は、相関関係だけでは終わらせずに因果関係まであると考えて、「アイスクリームの売上が増える ⇒ 水難事故が増える」とまでしてしまいますが、私達は今、相関関係と因果関係とを明確に区別していますから、そんなことはしません。
そこで、因果関係があるのかないのか調べることにします。因果関係があると考えられる場合には、まず相関関係がないといけません。
| (10.5.1)相関関係の発見 アイスクリームの売上が増加 かつ 水難事故の増加 アイスクリームの売上が増加しない かつ 水難事故の増加しない |
相関関係があるのならば、これが確認できるはずです。
で、統計の調査を調べてみると、この事実が確認されているんですね。つまり、相関関係があると言えます。
そこで、相関関係が因果関係なのかを調べる段階に入ります。因果関係があると言えるためには、
| (10.5.2)因果関係の特定 1.アイスクリームの売上の増加 ⇒ 水難事故の増加 2.水難事故の増加 ⇒ アイスクリームの売上の増加 |
の2パターンが考えられますが、こうして見ると、どうもどちらも正しくないような気がします。
「アイスクリームの売上の増加」が原因となって、「水難事故の増加」を結果として引き起こすことはちょっと想像がつきません。
また、「水難事故の増加」が原因となって、「アイスクリームの売上が増加する」という結果を引き起こすというのも常識的に考え難いです。
でも、そういう統計の数字があるのだから調べていくことにします。因果関係を調べるにあたっては、1.の場合なら「アイスクリームの売上の増加」以外の条件を、2.の場合なら「水難事故の増加」以外の条件をできるだけ変えないことが必要です。と言っても、現実の社会で、その他の条件を同じにして、「アイスクリームの売上」や「水難事故」のみを変えることなど無理です。その他の条件も変動するのは仕方ないので、一緒に変動する条件の数字も調べていくことにします。
調べていくと、「アイスクリームの売上が増加する」や「水難事故が増加する」ときに一緒に変化する要因が見つかります。
「アイスクリームの売上が増える」ときというのは、夏で、「気温が高い」ときなことに気付きます。
また、同じように、「水難事故が増加する」ときに一緒に変化する要因が見つかります。それも「気温」です。「水難事故が増える」のも、夏で、「気温が高い」ときであることに気付きます。
そうすると、「気温が高い」ことと「アイスクリームの売上の増加」に相関関係があることが分かります。
また「気温が高い」ことと「水難事故の増加」にも相関関係があることが分かります。
| (10.5.3)擬似相関の発見 アイスクリームの売上が増加 かつ 水難事故の増加 アイスクリームの売上が増加しない かつ 水難事故の増加しない 新しい相関関係の発見 気温が高くなる かつ アイスクリームの売上の増加 気温が高くなる かつ 水難事故の増加 |
夏ならば、「気温が高く」なり、「アイスクリームを買う人が増える」のは納得いきます。
また、夏で「気温が高くなる」と、海や川で遊ぶ人が増えるため、「水に関係する事故が増える」のも納得いきます。
だとすると、「アイスクリームの売上の増加」と「水難事故の増加」には直接的な関係はなく、実は、「気温の高さ」が両方ともに相関していることが分かります。
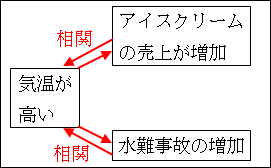
つまり、
「気温が高くなる」ことと「アイスクリームの売上が増加」に相関関係があり、
「気温が高くなる」ことと「水難事故の増加」に相関関係があり、
「アイスクリームの売上増加」と「水難事故の増加」は直接には無関係である、
というのが実際に起きていたことで、
「アイスクリームの売上が増加」と「水難事故の増加」に相関関係があるように見えていただけだということが分かりました。
これが擬似相関です。
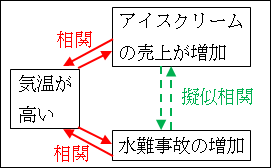
このように、
一見すると2つの対象に相関関係があるように見えるが、実は相関関係がなく、第3の要因によってその相関関係があるように見える事象が生じている
ことがあることに注意が必要です。
この擬似相関を相関関係や因果関係と考えるのは誤りです。
例えば、「アイスクリームの売上の増加」と「水難事故の増加」に相関関係があるから、「アイスクリームの販売を規制すれば、水難事故も減らせる」と考えるのはトンデモな主張になってしまいます。また、「水難事故を増やせば、アイスクリームの売上が上がる」と考えるのもトンデモな主張です。
以上、因果関係と相関関係の話でした。少し細かい所まで見たので、整理しておきます。
因果関係と相関関係の違いから整理します。
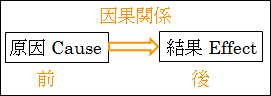
因果関係は、原因 C ⇒ 結果 E の関係です。
これは、原因 C が発生・変化することで、それに従って結果 E も発生・変化することを意味します。
時間的な前後関係から見ると、原因 C が前で、結果 E が後に発生・変化することを意味します。
図10.3.因果・相関・擬似相関
相関関係でも対象 X が発生・変化すると、同時に、対象 Y も発生・変化することを意味します。
このとき時間的前後関係は分かりませんので、X ⇒ Y かもしれないし、Y ⇒ X かもしれません。
図10.3.因果・相関・擬似相関
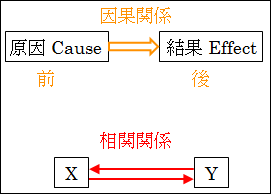
だとすると、因果関係と相関関係の共通点は、ある対象が発生・変化するときに、別の対象も発生・変化することが観察されることです。
そして、因果関係と相関関係の相違点は、時間的前後関係が明確か否かです。
因果関係では、共に発生・変化する2つの対象の時間的前後関係が明確で、原因 C が前に起きて、結果 E が後に起きます。
相関関係では、共に発生・変化する2つの対象の時間的前後関係が明確ではなく、X と Y のどちらが前に起きて後に起きるかが分かりません。
さらに、因果関係において、時間的前後関係が明確であることは、原因 C が結果 E を引き起こす構造が分かっているコトにも繋がります。
原因 C が、結果 E を引き起こしていると言うためには、どのような経路や手順を踏んでそうなっているのか説明する必要があります。とはいえ、この因果関係の構造を解明することは難しいので、時間的前後関係が分かるだけで終わる場合もあります。因果関係の構造が説明できないと因果関係があるとまでは言えないかもしれないが、無駄ということにはなりません。
因果関係と相関関係の区別がついたところで、相関関係と擬似相関の違いを明確にしながら整理します。
相関関係では、対象 X が発生・変化すると、同時に、対象 Y も発生・変化することを意味しました。
擬似相関も、対象 X が発生・変化すると、同時に、対象 Y も発生・変化しているように見えます。しかし、実際には、第3の対象 Z と、2つの X と Y とそれぞれ相関関係にあるだけで、X と Y との間には直接の関係はありません。Z の発生・変化と共に、X が発生・変化し、Y も発生・変化するために、X と Y に相関関係があるように見えていたということになります。
図10.3.因果・相関・擬似相関
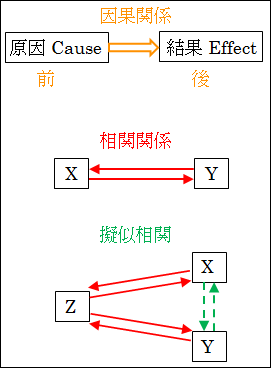
以上から分かることは、相関関係を中心にして因果関係と擬似相関に分かれている、ということです。
相関関係がある2つの対象において、時間的前後関係や構造を特定することで、因果関係となります。
相関関係があるように見える2つの対象が、実は別の要因によって発生・変化している場合は、擬似相関となります。擬似相関は、実際には相関関係がないので、相関関係から除外することになります。
図10.3.因果・相関・擬似相関
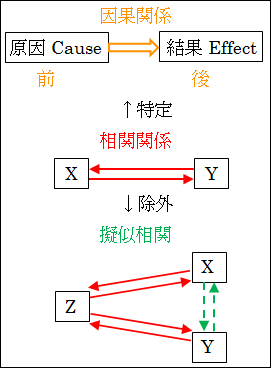
因果関係、相関関係、擬似相関の違いが分かったところで、論理的思考で特に重要な因果関係の特定に入ります。
まず、因果関係を特定する場合、対照実験が効果的でした。
対照実験では、最低2回の実験を行います。それぞれの実験では、1つだけ条件を変えて、それ以外の条件はすべて同じにして行います。1つも条件を変えずにすべて同じ条件で実験を行えば、同じ実験結果が得られるというのは言うまでもありません。そして、条件を1つだけ変えることで、異なる実験結果を得られれば、その変えた条件が原因で、異なる結果を導いたことが分かります。
図10.4.対照実験
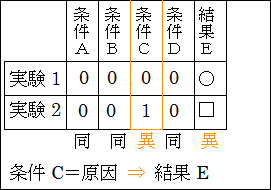
しかし、現実は複雑なために、厳密な対照実験が行える場合は少ないです。そこで、因果関係を特定するために、1歩ずつ手順を踏んでいくことにします。
いずれにしろ、因果関係があると言えるためには、相関関係があることが前提になっていました。ですから、いきなり因果関係を見つけに行くのではなく、まず相関関係から見つけることにします。因果関係は、時間的前後関係や構造等分析しないと分からないのに対して、相関関係なら、2つの対象 X と Y が同時に変化・発生していることさえ見つければ良かったです。要するに、因果関係よりも相関関係を見つける方が簡単なのです。
したがって、相関関係を発見した後に、因果関係がないか確認していくという順番をとります。
手順として大きく分けて、6段階になります。
| 1. 2つの対象に相関関係があるかの確認 2. 他の場合でも相関関係があるかの確認 3. 擬似相関等の除外 4. 時間的前後関係の特定 5. 因果関係の構造の特定 6. 一般的理論・法則と矛盾しないことの確認 |
最初の1~3は相関関係を見つけるものです。次の4~6は相関関係から因果関係を見つけるものです。
図10.5.相関関係から因果関係の特定
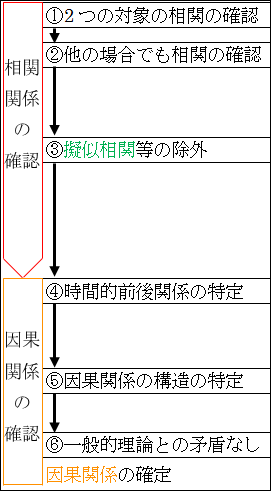
1. 2つの対象に相関関係があるかの確認
したがって、まず最初に、2つの対象に相関関係があることを確認します。
| Xが変化・発生する かつ Yが変化・発生する |
であることを観察します。Xが変化・発生しているとき、Yも変化・発生していることになります。これで、X と Y に相関関係がありそうだ分かります。
2. 他の場合でも相関関係があるかの確認
そもそも、すべての条件をそろえて実験することができないので、因果関係があるかではなく相関関係があるかを調べていたわけです。1つの条件下で調べた場合では、たまたま X と Y に相関関係がある、という結果が得られただけかもしれません。ですから、X と Y が様々な条件の下でも相関を示すことを確認しておかないといけません。
したがって、様々な異なる条件の下でも、
| X が変化・発生しない かつ Y が変化・発生しない |
であることも確認されればいいことになります。
図10.5.相関関係から因果関係の特定

3. 擬似相関等の除外
そして、様々な異なる条件の下に、相関関係があるかを調べているときに、注意しなければならないことがありました。擬似相関の存在です。
相関関係があるように見える場合でも、X と Y が変化・発生しているときに、一緒に変化・発生している対象 Z があると、擬似関係の可能性が高くなります。つまり、X と Y は直接は関係ないにもかかわらず、別の対象 Z によって、見せかけの相関関係が引き起こされているという可能性です。
この場合は、対象 X と Y は擬似相関であることを明確にして、相関関係がある、とは言わないようにしなければなりません。つまり、擬似相関は、相関関係から除外されることになります。また、偶然にも相関していたものも除外するのは言うまでもありません。
図10.5.相関関係から因果関係の特定
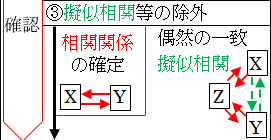
こうして、相関関係があるものに絞ることができます。
4. 時間的前後関係の特定
次に、相関関係があると分かったら、因果関係があるかを確認します。X ⇒ Y なのか、Y ⇒ X なのかを特定するということですが、ここでは、説明の便宜上 X ⇒ Y のみに絞ります。
X ⇒ Y と言えるためには、X と Y の時間的前後関係を明確にしないといけません。つまり、X が先に起きて、それに続いて Y が発生するということです。X と Y に相関関係があることを調べたときに、常に
| X ⇒ Y かつ 「Y ⇒ X」ではない |
であることを確認できれば良いことになります。
そうすると、相関関係にある X と Y の間に、「先に X が変化・発生して、その後に、必ず Y が変化・発生する」ことになります。「先に Y が変化・発生して、その後に、必ず X が変化・発生する」ことはないことも確認しておかないといけません。時間的前後関係が明確か否かがこれで確認できます。
図10.5.相関関係から因果関係の特定
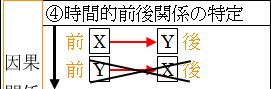
5.因果関係の構造の特定
時間的前後関係が分かったら、いよいよ原因によって結果が発生する構造が想定できるかの分析に移ります。X が原因となって Y という結果を引き起こす機能や構造を特定しないといけません。
図10.5.相関関係から因果関係の特定
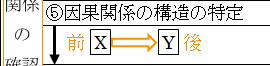
これが因果関係を特定するための一番の鍵です。この構造が掴めないと、相関関係があっても因果関係があるとはハッキリと言えないことになります。どういう経路や手順を踏むことで、原因が結果を引き起こしているのかという構造を分析します。
6.一般的理論・法則と矛盾しないことの確認
最後に、その因果関係が既存の理論や法則が矛盾しないかを確認します。
構造を分析して因果関係が特定できたと思っていても、既にある一般的な理論や法則に矛盾していると、その因果関係は誤っている可能性が高いです。もちろん、既存の理論や法則を修正する大発見の可能性もあるにはありますが、稀です。いずれにしろ、全体を総合した中で、その因果関係が矛盾なく機能するかは考えておかなければなりません。
図10.5.相関関係から因果関係の特定

このようにして、因果関係を特定します。
図10.5.相関関係から因果関係の特定
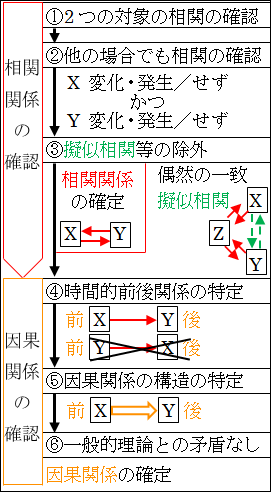
ですが、構造が分からない等の理由で因果関係が特定できない場合は、因果関係があるとは言わずに、相関関係がある、としておかなければなりません。
また、相関関係があると言ってきましたが、これを発見する場合、どれだけ観察すればよいのかとかいう問題は、統計学の範疇に入ってきます。数学を活用して、計算式から相関関係が強いか弱いか等を判断していくことになります。ここでは、統計学の内容に入りませんが、一応、統計学的な裏付けがあることは知っておいてください。統計学は数学を使うと聞くと、理系と思う人もいるみたいですが、いわゆる文系の学問でも必要になります。これは第III部 教養と学問・科学で説明します。
さらに、相関関係を分析して因果関係を特定するとき、実験や事例を多く重ねていることに気付くはずです。
実験や事例の積み重ねということは、経験であり帰納法であることと言えます。したがって、相関関係も因果関係も蓋然性でしかありません。つまり、因果関係がある確率が高いといったものです。これは仮説と同じですね。因果関係が証明されていても、因果関係があると言える確率が高い、というだけのこともあるということです。
ここまでの説明を聞くと、相関関係があっても、論理的主張には余り使えないように感じるかもしれませんが、そんなことはありません。
今まで見て来たように、相関関係の存在は、因果関係を探るためのヒントにはなります。また、因果関係までは特定できなくとも、何か問題 Y が起きる可能性があるとき、決まって X が起きることが分かっていれば、問題 Y に気付くことができなくても、X が発生していることに気付ければ予防策などを立てることができます。
さらに、因果関係がある気がして調べてみると、相関関係すらないことに気付ければ、それはそれで前進です。なぜなら、その因果関係や相関関係があるように思えていたのは、自分の思い込みや勘違いであることが分かるからです。
このように、因果関係と相関関係は、似て非なるもので、私達の論理的主張を誤らせる要因にもなりますが、正しく付き合えば、思考の手掛かりにもなるものです。
5 まとめ
以上、論理的思考の基礎を説明してきました。
論理的であることの形式面を支えるのは、様々な推論方法でした。結論と前提が、正しい推論方法によって展開していることが必要でした。
論理的であることの内容面を支えるのは、命題内部や命題相互の関連性でした。
そして、隠れた前提を補うことで、論理的の飛躍を抑え、その背後にある意図などを読み取るコトできました。
第 I 部 論理的思考の最後として、論理的思考で犯しやすい過ちや、議論の際に相手方が使ってくる詭弁等について次章で簡単に確認して終わりたいともいます。
前頁:第9章 弁証法
ページトップへ:第10章 論理的思考のまとめ
次頁:第11章 論理と誤謬