前頁 |▼| 次頁
第17章 論理ツリー ― how ツリー―
論理(ロジック)ツリーを用いて、課題の解決策の創出方法を学びます。
課題解決策を考えるための論理ツリーは how ツリーと呼ばれます。基本は前々章の what ツリーと変わりませんが、課題を解決するという目的意識の下に how ツリーを組み立てて行くことになります。
| 目次 |
| 1 課題解決と how ツリー 2 how ツリーの作成準備 3 how ツリーの作成 4 仮説設定 5 仮説検証と最適案の決定 6 まとめ テキストのダウンロード[詳細] 通常版 既述版 配布資料 |
| ADs |
1 課題解決策と how ツリー
why ツリーで問題の原因が特定できたら、後は課題化してやれば課題形成段階は終わります。こうして、解決すべき課題が明確になったら、課題を解決するにはどうすればよいかを考える段階、すなわち、解決策立案段階になります。
解決策を考え出して、具体的な方策を組み立てるのに役立つのが、またしても論理ツリーです。
このとき使う論理ツリーは、課題をどうやって解決するのかを考えるので、how ツリーと呼びます。何故 how ツリーと呼ぶのかは、how が「どうやって」や「どのようにして」といった意味であることからも容易に想像できるはずです。
したがって、この解決策を考え出すのが、how ツリーを作る際の目的意識になります。
そして、「どうやって解決するのか」という問いを繰り返しながら、課題の解決策を考えて行くことになります。
why ツリーが「なぜ?」という問いを繰り返していたのに対して、how ツリーは「どうやって?」という問いを繰り返します。
ところで、なぜ論理ツリーが解決策を考え出すのに役に立つのでしょうか。
今、結論ありき的に、論理ツリーが解決策を考え出すのに役立つと説明しましたが、論理ツリーを万能の道具と過信しないためにも、その理由を理解しておく必要があります。
この役立つ理由は結構簡単なことです。
課題に対する解決策は、課題を解決できることが最低限の条件として求められます。
課題が解決できないと、そもそもの意味がなくなってしまいます。
したがって、解決策は、課題の解決に効果的であることが求められます。課題の解決に効果がない策は、そもそも意味がありません。
また、課題に対する解決策に求められることは、ただ課題が解決できるだけではなく、できるだけ安くて速いことが求められます。
効率的ではない策、つまり、無駄の多い策は、たとえ課題を解決できたとしても、大変な時間と費用の無駄を発生させます。
したがって、解決策は、課題の解決に効率的であることが求められます。
この2つの効果と効率という観点を踏まえると、論理ツリーの特性が有効に働くことが分かります。
論理ツリーを作るとき、常に MECE(ダブりなくモレなく)に分解することが意識されています。ですから、論理ツリーによって解決策が導ければ、課題の解決策の候補をダブりなくモレなく検討できます。
したがって、MECE に分解できることで、より効果的で、より効率的な解決策を選ぶことができるのだと分かります。
こうした理由から、課題解決策を考えるのに how ツリーが活躍することが分かります。
2 how ツリーの作成の準備
それでは早速、how ツリーを作ってみましょう。この章で学ぶことが how ツリーであり課題解決策の立案方法なので、今回は問題の原因がほとんど明らかな状態から開始します。実際には、問題の本質的原因を特定する課題形成段階を経ていることを改めて注意喚起をしておきます。(17.1)を見てください。
| (17.1)高校生の太郎は、学校の勉強を真面目にしており、試験の成績も良い。しかし、自分の頭で何かを考えることに苦手意識がある。例えば、教科書に載っているような事柄を問われれば、すぐに答えることができるが、1つに決まる答えがないような問題に対して、自分の意見を論理的に組み立てたり、説得的に述べることができない。そこで、太郎は、論理的思考力を鍛えたいと考えた。考えられる解決策を論理ツリーを用いて示せ。 |
(17.1)の問題文から読み取れることを整理します。
問題だと感じていることは、「太郎は自分の頭で考えることが苦手だ」ということです。
さらに、その原因は、「知識が足りない」ことではなく、「論理的思考が弱いからだ」ということが分かっています。
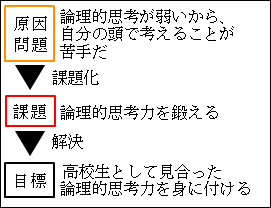
したがって、本質的な原因、あるいは、本質的な問題は、「論理的思考が弱いから、自分の頭で考えることが苦手だ」と分かりました。
図17.1.課題と解決された状態の設定

これを課題化します。
解決すべき課題は、「論理的思考を鍛える」ことだということになります。
図17.1.課題と解決された状態の設定

したがって、「論理的思考を鍛える」という課題をどうすれば解決することができるのかについて考えて行きけばいいことになります。
しかし、課題が分かり、この課題を解決すればいいからといって、いきなり解決策を考え始めるのは早計です。
「課題が解決した」とはどういったことなのかを考えておかないといけません。
課題が解決した状態が分からないと、解決策が効果があるかないかが判断できません。ですから、課題が解決した未来を明確にしておきます。これは、理想の状態を明らかにすることであり、それが目指す目標となります。
それでは、目標たる課題が解決された状態を明確にしておきましょう。
「太郎」は「高校生」です。ですから、最低限の目標として、「高校生として見合った論理的思考力が身につく」ことと設定します。
したがって、「論理的思考を鍛える」という課題が解決されれば、「高校生として見合った論理的思考力が身に付く」という目標が達成されることになります。
図17.1.課題と解決された状態の設定
目標も分かったところで、how ツリーを作ろうと考えてしまいますが、まだ準備は終わっていません。
how ツリーを作る前に、もう少し厳密に前提条件を確認しておきます。
前提条件を確認しておかないと、思考が拡散していくことになり、最悪の場合何でもありになってしまい、収拾がつかないことになるからです。本来は、こうした前提条件は、原因を特定するための課題形成段階である程度に明らかになっているはずですが、今回は問題の説明の便宜上、改めて確認しておくことにします。
「学校の勉強を真面目にしており、試験の成績も良い」こと、「教科書に載っているような事柄を問われれば、すぐに答えることができる」ことから、「知識面は高校生としては問題がなく十分な水準である」ことが分かります。
ですから、「知識の吸収よりも、論理的思考を伸ばす解決策を考える」ことが必要だと分かります。
| <前提条件1> 知識の吸収よりも、論理的思考を伸ばす解決策を考える |
「論理的思考力」が何を意味するかも確認しておきます。課題が「論理的思考力を鍛える」ことなので、「論理的思考」についてしっかりと分かっていないと話が始まりません。
この講義では、ずっと「論理的思考」とそれを使った「問題解決」を目指して説明して来たので、今更な話になります。
「論理的思考」は「正しい推論」と「正しい知識」によって成り立っていました。
そして、「推論」は「前提」から「結論」を導くことでした。
「前提」は「事実」や「科学的な知識」といったものでした。
この「前提」から何かしらの「結論 」を導くことで、1つの論理的な主張となります。
こう考えると、前提条件として「知識の吸収よりも、論理的思考を伸ばす解決策を考える」があるので、「推論」の能力を鍛えることが必要だと分かります。
したがって、前提条件に「推論の能力を上げることに集中する」を付け加えておきます。
| <前提条件1> 知識の吸収よりも、論理的思考を伸ばす解決策を考える <前提条件2> 推論の能力を上げることに集中する |
このように、今回は、「論理的思考力を鍛える」という課題は、主に「推論の能力を鍛える」ことでもあることが分かります。
さて、何が解決すべき課題なのか、課題が解決されたらどうなるのか、解決策を考えるにあたっての前提条件は何かが分かったので、いよいよ実際に解決策を論理ツリーを使って考えてみましょう。
3 how ツリーの作成
目標の明確化と前提条件の確認をしたので、解決策の作成の準備が終わりました。それでは、いよいよ実際に解決策を考えて行きましょう。
論理ツリーの中の how ツリーを使い、「どうやって?」と問いながら論理を構築して解決策を考え出して行きます。
今回で言えば、課題の「論理的思考力を鍛える」って「どうやって?」と問うことになります。
しかし、いきなり「どうやって?」と訊いても、おそらく上手いこといい案が浮かんでこないはずです。何か枠組みが必要です。
だけど、実際にやってみれば分かりますが、最初から適切な枠組みが思い浮かぶことも中々ないでしょう。具体的に何をすべきか未だよく分かりません。
「論理的思考力を鍛える」という抽象的な命題から、具体的な方法を導くための適切な枠組みが上手く思いつかないので、枠組みに囚われるのではなく、具体的なものを考えてみて、適切な枠組みを考え出していくことにします。
つまり、「論理的思考力を鍛える」には「どうやって?」と最上位命題を大きく分解していくトップダウン(逆算)方式で考えるよりも、具体的に「何をするのか?」という積み上げる視点であるボトムアップ(積み上げ)方式で具体的に何があるか少し考えてみることにします。
すぐに思い浮かぶのは、「自分で考えられるようになるために、本を読め」という言葉です。
皆さんも、教師を始めとして多くの大人に「本を使う」ことを勧められたことがあるのではないでしょうか。確かに、本は色々と考える切っ掛けや、考え方の指針を示してくれることがあります。
「本を使う」ことを課題解決の候補の1つとして挙げておきましょう。
| 論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) 本を使う |
他には、最近よく言われているディスカッションやディベートといったものが比較的思いつきやすいのではないでしょうか。要は「議論する」ことです。「議論する」ためには、感情論にならずに論理的に話すことが大切になります。
「議論する」も課題解決のための候補の1つとして挙げられるでしょう。
| 論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) 本を使う 議論する |
こうして具体的な解決策を考えて、即座に、「本を使う」か「議論する」かという枠組みを思いついて当てはめてはいけません。
その理由の1つとして挙げられるのが、「本を使う」か「議論する」かという枠組みが、「論理的思考力を鍛える」手段として必然的な分解方法なのか分からないことです。
加えて、MECE(ダブりなくモレなく)に分解するとき、上位階層に適用する枠組みは、できるだけ一般的・抽象的なものの方が良かったことも理由に挙げられます。
ですから、「本を使う」ことと「議論する」ことが思いついたなら、もう少し一般的・抽象的で MECE に分解できるような枠組みがないか考えてみます。
「本を使う」場合と「議論する」場合を対比して相違点を見つけ出しましょう。
ここで、「本を使う」場合は、自分独りでも実行が可能であり、「議論する」場合は相手が必要となることに気付きます。
つまり、「自分独りで鍛える」か「他人と鍛える」かという枠組みが考えられます。
| 論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) 本を使う → 自分独りで鍛える 議論する → 他人と鍛える |
これなら、「他人と鍛える」が、「自分独りで鍛える以外」つまり「自分独りで鍛えるのではない」の言い換え表現なので、「そのもの」か「それ以外」かの枠組みの変形だから、MECE に分解できていることが分かります。
そして、「自分独りで鍛える」か「他人と鍛える」かという枠組みは、上位階層に適用してもよさそうなくらい、かなり一般的・抽象的です。
「自分独りで鍛える」ことは、「本を使う」以外にも色々と思いつきそうですし、「他人と鍛える」ことも、「議論する」以外にも色々と思いつきそうです。つまり、「自分独りで鍛える」か「他人と鍛える」かは、複数の事柄を含み得る広い命題だと分かります。ですから、かなり一般的・抽象的な枠組みになっています。
これで、最初の枠組みとして、「自分独りで鍛える」か「他人と鍛える」かという枠組みができました。
この「自分独りで鍛える」か「他人と鍛える」かという枠組みを、最上位命題の「論理的思考力を鍛える」に適用します。
つまり、「論理的思考力を鍛える」って「どうやって?」と問いに対して「自分独りで鍛える」ことによって、あるいは、「他人と鍛える」ことによって、と答えを返すことになります。
図17.2.解決策の立案 画像クリックで拡大

「自分独りで鍛える」場合から考えて行きます。
「自分独りで鍛える」場合の現在思いついている典型例が、「本を使う」ことでした。
そのまま「自分独りで鍛える」には「どうやって?」と問い、「本を使う」ことでと答えを返せば、具体化して階層を掘り下げることができます。
ただ、これではわざわざ論理ツリーを作る意味がないでしょう。
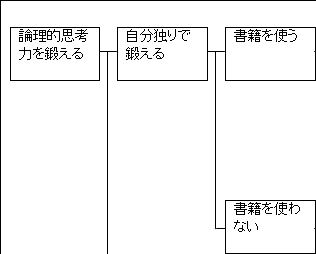
「本を使わない」場合も考えたいところです。ですから、「本を使う」か「本を使わない」かという枠組みで、「本を使わない」場合も後で考えられるようにしておきます。
したがって、「書籍を使う」か「書籍を使わない」かという枠組みを当てはめて考えてみましょう。
なお、もちろん、この枠組みが上手く行くかは分かりません。分解して行って不都合が生じれば、再び考え直すことになります。
図17.2.解決策の立案 画像クリックで拡大
「書籍を使う」場合について考えます。
階層を掘り下げて行っても忘れてはいけないのは、上位階層が下位階層を縛っていることです。
常に最上位命題、かつ、解決すべき課題である「論理的思考力を鍛える」ために、「書籍を使う」って「どうやって?」と考えることです。
また、無暗矢鱈と思考を発散させないように注意しないといけません。
前提条件に、「知識の吸収よりも、論理的思考を伸ばす解決策を考える」ことがあることを意識しておいてください。もし「知識を仕入れたり、覚える」ために「書籍を使う」という方向に思考が引っ張られてしまうと、「推論の能力を上げることに集中する」はずの「論理的思考力を鍛える」という課題の解決から離れてしまうことになります。それは即ち、課題解決に効果的な策から離れて行くことになります。
それでは、「書籍を使う」ことで、どのように「論理的思考力を鍛える」ことができるでしょうか。
「書籍を使う」ことで、「論理的思考力を鍛える」って、「どうやって?」と問います。
「知識の吸収よりも、論理的思考力を伸ばす解決策」として「書籍を使う」場合には、「書籍を読み、その論理を追う」ことになります。
図17.2.解決策の立案 画像クリックで拡大

「書籍を読み、その論理を追う」ことは、要は、前提と結論を明らかにしつつその関連性や隠れた前提を見つけ出しながら読むことになります。教科書に載っていることを天下り的に覚えて来た太郎君にとっては少し骨が折れることでしょうが、一応解決策の1つとして「書籍を読み、その論理を追う」が考え出せました。
なお、「書籍を読み、その論理を追う」という命題は、上位階層である「書籍を使う」を MECE に分解したというよりは、具体化して掘り下げたものになります。
さらに続けて、「書籍を読み、その論理を追う」ことを掘り下げていきましょう。
「書籍を読み、その論理を追う」って「どうやって?」と問います。
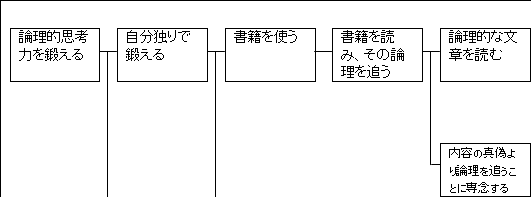
まず一番簡単に思いつくのは、「論理的な文章を読む」ことかと思います。
「論理的思考力を鍛える」のだから、「論理的な文章を読む」ことが必要であるのは想像に難くありません。
また、「書籍を読み、その論理を追う」ためには、「内容の真偽よりも論理を追うことに専念する」ことも必要になります。
図17.2.解決策の立案 画像クリックで拡大
ここで、あることに気付きます。
それは、第5階層が、「どうやって?」つまり how? と訊いているというよりは、「何を?」つまり what? と訊くことで分解されているということです。
具体的な方法や手段を問うことで、how ツリーは作成されます。しかし、具体的な方法や手段を how? と問い続けて行くと、段々その方法や手段を実行するための具体的な作業や手順となっていきます。そうすると、how? という問いは、what? という問いに近くなり区別がつかなくなり、途中で what ツリーに切り替わることがあります。なお、what ツリーは、構造や概念の整理や分析のために使われました。
今、「書籍を読み、その論理を追う」ためには、「どうやって?」と問い、「論理的な文章を読む」と「内容の真偽よりも論理を追うことに専念する」と分解しました。
しかし、注意して考えると、「論理的な文章を読む」ことと「内容の真偽よりも論理を追うことに専念する」ことは、二つで一つです。
つまり、読む対象は「論理的な文章」であり、気を付ける点が「内容の真偽よりも論理を追うことに専念する」ということです。
「論理的な文章を読む」ことを行う場合には、「内容の真偽よりも論理を追うことに専念する」ことをしないということではありません。
その逆の、「内容の真偽よりも論理を追うことに専念する」ことを行う場合に、「論理的な文章を読む」ことをしないこともありません。
「論理的な文章を読む」、かつ、「内容の真偽よりも論理を追うことに専念する」ことを同時に行わないといけなません。
つまり、第5階層の2つの命題は、どうやって「書籍を読み、その論理を追う」のか? ということに答えてはいます。しかし、ここまで具体的になると、「書籍を読み、その論理を追う」ことを実行するために、具体的に何をするのか?、という作業を問うていることと同じになっています。
つまり、「書籍を読み、その論理を追う」という具体的な手段の構造を分析してするべき作業を分析していることになります。
これは、「どうやってするのか?」という問いと「何をするのか?」という問いの区別がもうつかなくなっています。how? なのか what? なのかの区別がつかなくなっています。
ですから、how ツリーを作っているはずなのに、途中から what ツリーの作成に切り替わってしまっていることを意味します。
ですから、ここまで掘り下げたら、how ツリーで具体的な解決策の方向性を考え出すことは一応達成できたと見なしてもいいです。
how ツリーが what ツリーに切り替わっていることを確認するために、念のために更にもう一階掘り下げてみましょう。
第5階層の「論理的な文章を読む」をどうやって? と更に掘り下げてみます。
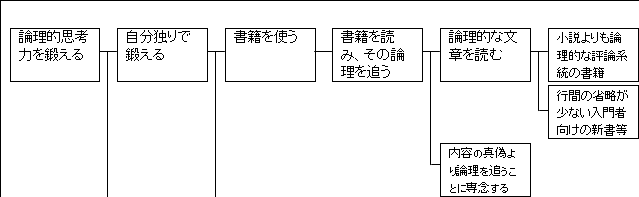
そうすると、「論理的な文章」だから、小説や文学よりも論文や評論の方が適切かなと思えます。
ですから、「小説よりも論理的な評論系統の書籍」と具体化できます。
また、「太郎が高校生」ということも考慮して、そんな高度な内容は扱いきれないと考えられます。
ですから、「行間の省略が少ない入門者向けの新書等」を使うべきだと考えられます。
図17.2.解決策の立案 画像クリックで拡大
また、「内容の真偽よりも論理を追うことに専念する」を掘り下げて具体化すると、「前提と結論に分ける・隠れた前提を補う」ということをすればいいです。
図17.2.解決策の立案 画像クリックで拡大
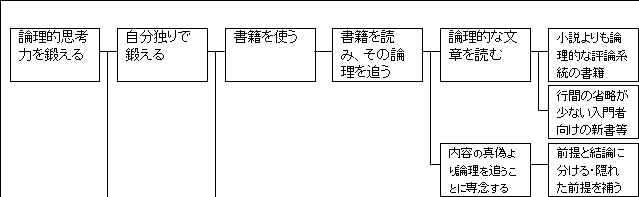
こうやってみると、「論理的な文章を読む」を分解した「小説よりも論理的な評論系統の書籍」と「行間の省略が少ない入門者向けの新書等」は、「どうやって?」how? ではなく、「何を?」what? の答えと言った方が良さそうです。
このように、how ツリーを掘り下げて行くと、途中から what ツリーになってしまう、あるいは、what ツリーと区別がつかなくなったりします。これは、すべての論理ツリーの特性として、階層が下がれば下がるほど具体的な作業や物事になっていくためです。
ですから、how ツリーを作る際には、常に「どうやって?」how? と考えていって、階層がある程度下がった段階で、「何を?」what? と区別がつかなくなっても構いません。それは、ある意味では、how ツリーが十分に具体化された証拠とも言えます。
ただし、こう言うと、how ツリーを作っているのに、不用意に what? と問いながら進める人がいるのですが、それはやめてください。
how ツリーを作る際には、「どうやって?」how? と問わなければいけません。さもないと、目的からズレた解決策が生み出される危険が高まります。したがって、一般性や抽象性が高い上位階層の段階で「何をするのか?」what? と考えないようにしてください。
そもそも、what ツリーは、構造や概念を整理し分析するための論理ツリーです。
解決策の方向性が具体的になっていない段階で、what ツリーに切り替わってしまうと、有り得る解決策がすべて出そろう前なのに、漠然とした解決策をどうやって実行するのかという論理ツリーが作られてしまう可能性が出てきます。
つまり、色々な有り得る解決策を考えているのではなく、ある1つの解決策の構造や手順を分析してしまっているということになります。
ですから、how ツリーの階層が十分に掘り下げられて、結果として、what? と how? が区別がつかなくなるのはいいですが、解決策の基本的方向性を考えている段階では、「何をするのか?」ではなく「どうやってするのか?」を強く意識するようにしてください。
以上、「何をするのか?」what? と「どうやって?」how? の区別がつかなくなるのは、十分に具体的になった結果である、これを心に留めておいてください。
ちなみに、what ツリーになると、解決策を実行するための具体的な作業や手順を分析することになるということから分かる通り、what ツリーは、実行すべき解決策を決定した後の実行計画を立てる際には非常に有益です。これは後で説明します。
▼批判的思考の話を飛ばす
ここで、how ツリーの話から少し逸れたついでに、批判的思考について話したいと思います。第5階層を見てください。
「内容の真偽よりも論理を追うことに専念する」と言うと、誤った事実を見過ごしてもいいのか、という疑問が生じるかもしれませんが、もちろん通常は誤った事実を見過ごすていいはずがありません。
ただし、今回は「論理的思考力を鍛える」ための解決策を考えており、「知識を吸収するよりも、論理的思考力を伸ばす解決策を考える」という前提条件もあります。
ですから、「前提や結論自体が事実と合致しているのか?」という視点から考えるのを敢えて控えています。そして、前提が正しいと一旦仮定してしまって、前提が結論を正しく支えている論理になっているかを主に考えます。また、正しく支えていないなら、どういう論理なら正しくなるのかといったことを考えます。これは論理の正誤に意識を集中させていることが分かります。
何故こんなことをするのかと言えば、時間や労力の節約のためです。
「論理的思考力を鍛える」ことに集中したいのに、前提の真偽までこだわると、「結論を導くための前提に置かれている知識や情報、事実などが本当に正しいのか?」と考えて調べることになってしまいます。そうすると時間が驚くほど必要になります。
したがって、論理自体の力を養いたいのに、知識の吸収にかなりの時間を費やす必要があります。これでは、課題である「論理的思考力を鍛える」ことからズレてしまっています。
「内容の真偽」は、論理だけではなく「前提の正しさ」も関係しています。その前提の正しさは、主に「知識の正しさ」に関係します。そして、前提条件から「知識の吸収」は二の次になります。
そこで、「論理的である」ことの利点は、前提が正しいならば、結論は必ず正しくなることです。この性質を利用して、前提を正しいものと仮定してしまって、前提が結論を正しく支えている論理なのかどうかを考えることに集中しようという意味で、「内容の真偽よりも論理を追うことに専念する」としています。
なお、注意してもらいたいのは、論理的思考 logical thinking と言うと、前提に置かれている知識や情報、事実などが正しいことが含まれた意味で通常は使われます。私も今回を除いて基本的には、論理的思考と言うときには、前提の正しさを当然含んだものとして使っています。ですから、論理的に考えるときには、論理と推論の正しさに加えて、必ず前提が正しいのかも検討しないといけません。
この論理の正しさだけではなく、「前提になっている知識や情報、事実などが正しいのか?」と考える場合を批判的思考と呼ばれます。つまり、事実や情報の正しさを問いながら、批判的に考えることです。批判的思考は英語では、critical thinking と言います。
日常生活では、「批判」と言うと、非難したり、悪口を言ったりという意味に捉えられることもありますが、「批判」の元々の意味は、「物事に検討を加えて、判断・評価すること」です。「批」が、「つき合せて良し悪しを決める」という意味があります。これに判断する、判定する等の「判」と組み合わせて、「批判」となります。「批評」も似た意味で使われますね。
言うまでもないかもしれませんが、批判的思考でも当然に論理の正しさは求められることが多いです。ですから、論理的思考と批判的思考は、使う人によっては、ほぼ同じ意味で使われたりします。敢えて相違点を明確にするなら、
論理的思考が、前提と論理の正しさの両方を考えながら、論理的に正しいかを考えて行くことの重要性を強調しているのに対して、
批判的思考は、前提と論理の正しさの両方を考えながら、前提に置かれている知識や情報、事実などが正しいかを考えて行くことの重要性を強調している
と考えていれば基本的には大丈夫です。
あるいは、論理的思考は批判的思考によって可能となる、と考えてもいいです。
論理的に読解したり、分析したり、研究したり、表現したりするためには、論理的思考が当然に求められます。この講義では、論理的思考ができるようになるために、論理的とはどのようなものか、どのようにすれば論理的になるのかと具体的に詳しくずっと説明して来ました。そして、前提に結論に論理にすべてに本当に正しいのか? と考える批判的思考は、論理的思考を実践するのに役に立ちます。「これは正しいのか?」と常に批判しながら考えることで、正しい知識と正しい推論が形成されるので、論理的になります。
批判的思考は、このように人によって捉え方が微妙に異なりますが、いずれにしろ、物事を批判的に思考することという点では共通しています。
後、補足として、批判的思考 critical thinking と称して、揚げ足取りや粗探しをする人が偶にいます。詭弁や誤謬を探すのに批判的思考という姿勢は非常に有効ですが、行き過ぎると自分が詭弁や誤謬を犯すことになり得ます。ミイラ取りがミイラにならないように気を付けてください。批判的思考にしろ論理的思考にしろ、使う目的は建設的で効果的な議論をするためであり、相手に難癖をつけるためではありませんから。
▲批判的思考の話に戻る
さて、話を how ツリーの作成に戻します。
次に「書籍を使わない」場合について考えます。「書籍を使わない」で「論理的思考力を鍛える」にはどのような方法があるでしょうか。
図17.2.解決策の立案 画像クリックで拡大
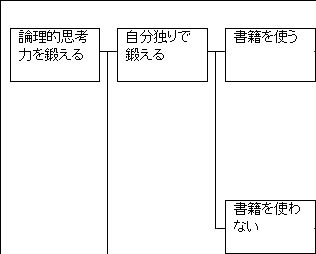
「書籍を使わない」で考えるといっても、何か考えるネタがないと考えることができません。考えるネタになりそうなものを思い浮かべてみます。
新聞やテレビ、インターネットといったメディアから入ってくる「ニュース」が考えるネタになりそうです。
| 書籍を使わないで、論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) ニュース |
また、自分の「身の回りの出来事」といった些細なことでもいいでしょう。
例えば、太郎の友人の花子が泣いていたのは何故なのか?、といった具合に考えるなどです。
| 書籍を使わないで、論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) ニュース・身の回りの出来事 |
他にも、正義とは何か、道徳的とは何か、といった「抽象的な概念」について考えることもあるでしょう。
| 書籍を使わないで、論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) ニュース・身の回りの出来事 抽象的な概念 |
さらには、もしこの世に重力が無かったらどうなるのか、もし生身の人間が空を飛べるとしたらどうなるのか、といった「非現実的な事柄」についても考えることができます。
| 書籍を使わないで、論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) ニュース・身の回りの出来事 抽象的な概念・非現実劇な事柄 |
こうして見ると、考えるネタは「身の回り」のことから「有り得ない」ことまで色々あります。これを全部一緒にして考えてもいいですが、「論理的思考力を鍛える」ための効果的で効率的な手段を考えているのだから、考える対象をその性質によって分けておきましょう。
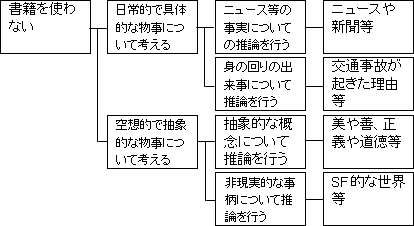
「ニュース」や「身の回りの出来事」といったものは、「日常的で具体的な物事について考える」ことと抽象化してまとめられます。
「抽象的な概念」や「非現実的な事柄」といったものは、「空想的で抽象的な物事について考える」ことと抽象化してまとめられます。
| 書籍を使わないで、論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) ニュース・身の回りの出来事 → 日常的で具体的な物事について考える 抽象的な概念・非現実劇な事柄 → 空想的で抽象的な物事について考える |
そして、「日常的で具体的な物事について考える」ことと、「空想的で抽象的な物事について考える」ことは、 MECE に分解された枠組みであることを確認します。
まず、文言を見てみると「日常」と「空想」が反対の意味になっています。「空想」が「非日常」であるからです。
さらに、「具体的」と「抽象的」が反対の意味になっています。これは今まで散々と使ってきた概念なので、詳しい説明は不要でしょう。
したがって、「日常的で具体的な物事」と「日常的で具体的な物事以外」とに分けたら、「日常的で具体的な物事以外」が「空想的で抽象的な物事」に言い換えられます。
このことから、「そのもの」か「それ以外」かの枠組みが変形された枠組みとなっているのが分かります。
ですから、「日常的で具体的な物事について考える」か「空想的で抽象的な物事について考える」かという枠組みを、「書籍を使わない」場合に適用します。
図17.2.解決策の立案 画像クリックで拡大
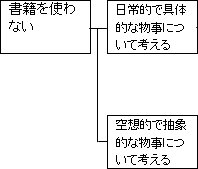
さらに掘り下げる上で先程枠組みを作るために使った具体例を再利用しましょう。
| 書籍を使わないで、論理的思考力を鍛えるには? ボトムアップ方式(具体例を考えてみる) ニュース・身の回りの出来事 → 日常的で具体的な物事について考える 抽象的な概念・非現実劇な事柄 → 空想的で抽象的な物事について考える |
「日常的で具体的な物事について考える」場合の下位階層については、具体的に「どうやって?」と訊かれれば、「ニュース等の事実について推論行う」ことによってや、「身の回りの出来事について推論を行う」ことによってと答えることができます。
「空想的で抽象的な物事について考える」場合の下位階層については、具体的に「どうやって?」と訊かれれば、「抽象的な概念について推論を行う」ことによってや、「非現実的な事柄について推論を行う」ことによってと答えることができます。
図17.2.解決策の立案 画像クリックで拡大
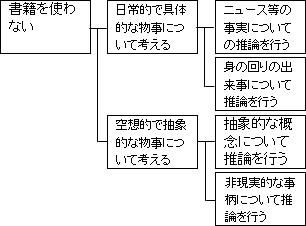
これ以上下位階層に掘り下げても、「どうやって考えるの?」という how? で問うと言うよりも、「何を考えるの?」という what? で問うようになってしまいます。実際、各命題を掘り下げると具体例になります。
図17.2.解決策の立案 画像クリックで拡大
what ツリーになり、十分に具体的になったので、一旦「書籍を使わない」場合についての掘り下げは終えます。今は、具体的な作業や実行手順を考えているのではなく、解決策をダブりなくモレなく挙げることが目的で how ツリーを作っているからです。
では、「他人と鍛える」場合について考えます。
「他人と鍛える」場合の現在思いついている典型例が、「議論する」ことでした。
そのまま「他人と鍛える」には「どうやって?」と問い、「議論する」ことで、と答えを返せば、具体化して階層を掘り下げたことになります。
ただ、やはり、これではわざわざ論理ツリーを作る意味がありません。上手く行くかは分かりませんが、「議論する」か「議論しない」かという枠組みを当てはめて考えてみましょう。
しかし、「議論しない」で「他人と論理的思考力を鍛える」って「どうやって?」と訊かれると困ります。
ここで、図書館やファミレス、喫茶店などで、学生が友達と一緒に勉強している姿から、友達と一緒にその場で本を読む、とかが挙げられるだろうと考えた人は待ってください。
確かに、この場合、議論はしていません。が、それは友達と一緒にその場にはいますが、勉強自体は独りでやっています。これでは、「自分独りで鍛える」場合と何ら変わりません。別に「自分独りで鍛える」か「他人と鍛える」かという枠組みは、どこで誰と居ようが関係ない枠組みです。
「自分独りで鍛える」ために、本を読んでいる横に友達が別に勉強していたからといって、「他人と鍛える」ことにはなりません。「他人の傍や視線がある中で勉強する」ことは集中力を上げる手段としては考えられますが、「論理的思考力を鍛える」こと自体には関係がありません。
色々考えてみても、「議論しない」ことで、「他人と論理的思考力を鍛える」という手段は思いつきません。
そこで、「議論する」か「議論しない」かという枠組みが、今回は適切ではなかったからだ、と考えて、別の枠組みを考えることにします。
改めて「論理的思考力を鍛える」ために「他人と鍛える」って「どうやって?」と問います。
「他人と鍛える」と言ったとき、「他人」にも色々な種類があります。典型的で身近なのは、家族を別とすれば、同級生の友達や先輩や後輩、そして教師などの知り合いが挙げられます。
これに注目して、「他人と鍛える」を、「友人等の知人以外と鍛える」か「友人等の知人と鍛える」かの枠組みで分けます。
図17.2.解決策の立案 画像クリックで拡大

「知人以外と鍛える」場合について考えます。
「知人以外と論理的思考力を鍛える」って「どうやって?」と考えると、「議論する」以外にも思いつきます。
今、この講義を受けているので、分かりやすいかと思いますが、「教えてもらう」ことによって、「知人以外と論理的思考力を鍛える」ことができます。
学校でも、それ以外でも私達は、「人から教えてもらう」ことがよくありますし、これは比較的思いつきやすいのではないでしょうか。
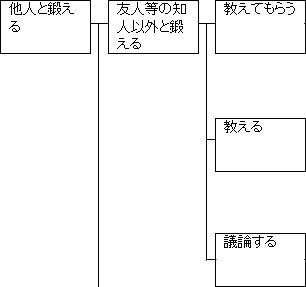
「教えてもらう」が思いつければ、逆に「教える」ことも簡単に思いつけるかと思います。
そうすると、「議論する」ことと、「教えてもらう」ことと、「教える」こととの3つに分解できそうです。
図17.2.解決策の立案 画像クリックで拡大
なお、ここまで掘り下げると、かなり具体的な方法へと落とし込まれているので、「そのもの」か「それ以外」かの枠組み等を使って MECE に分解することが難しくなってきます。が、それで構いません。
解決策は本当に色々あり、微妙な違いしかないものだったりする場合も多いです。そうした微妙な違いまですべて厳密に MECE に分解することに拘ると、時間がかかり過ぎます。微妙な違いしかないことをダブっていると言うのなら、少し位ならダブっても(not ME)構いません。
how ツリーでは、MECE に分解することを意識しつつも、ある程度掘り下げって行ったら、最終的にはできるだけモレなく(CE)分解できていればよしと考えてもらっていいです。
どの解決策を選ぶかというときに、検討していない解決策が無いことが大切だからです。
例えば、「議論する」と「教えてもらう」という範疇(カテゴリー)を比べてみてください。
「教えてもらう」場合も、「議論する」ことが含まれることが多いです。
「教えてもらう」ときに、講義を聴くだけではなく、講師に質問したりします。逆に、講師がこちらが理解しているか問いかけて来て、答えさせたりすることも普通にあるはずです。さらには、この講義ではしていませんが、隣の席の人と話し合わせたり、集団をつくらせて議論する場合もあります。
この考えると、「議論する」ことと「教えてもらう」こと、この2つの範疇(カテゴリー)は少なからずダブっています。
しかし、「議論する」ことの重点が、「人と話し合いながら、相手に反論したり反論されたりすることで自分の論理的思考力を鍛える」ことにあり、
「教えてもらう」ことの重点が、「講義で人に教えてもらい、導いてもらいながら論理的思考力を鍛える」ことにあるとすれば、
多少のダブりはあっても、異なる解決策と言えます。
「議論する」方法では、かなりの部分で自分で修正点等に気付かないといけませんが、「教えてもらう」方法では、講師が自分の不足している分野等を上手く補って導いてくれるはずです。
このように、how ツリーでは、MECE に分解しつつも最終的に少しダブっても(not ME)、モレがなければ(CE)良いと考えてもいいです。
▼why/how と MECE の関係を飛ばす
さらに、一応の補足として、why ツリーを作るときも、情報が完全に揃うことも、現実を過不足なく切り分けることも、実際にはほとんどできません。
why ツリーを作る目的は、複雑で難解な問題をできるだけ切り分けて小さくすることで考えやすくするためでした。
ですから、why ツリーでも完全に MECE に分解できるとは限らず、厳密には MECE になっていなくてもよし、とすることも有り得ますし、実際あります。
しかしながら、問題の原因の特定は、本質的な問題に繋がっており、かなりの精度で分析ができていなければならないので、how ツリーよりも MECE であることが強く求められます。
逆に言えば、 why ツリーと比べれば、how ツリーは本質的な問題を解決できればいいので、少々 MECE でなくても構わないと考えられます。
また、why ツリーで分析する問題の型は、「発生型」の問題でした。これは MECE に分解しやすい問題の種類です。それ以外の MECE に分解することが難しい問題は、後で説明する因果関係図や論理ピラミッドで分析することになります。
▲why/how と MECE の関係に戻る
話を戻します。「友人等の知人以外と鍛える」ことを「教えてもらう」、「教える」、「議論する」ことの3つを順番に考えて行きます。
まず、「教えてもらう」についてからです。
「知人以外に教えてもらって論理的思考力を鍛える」って「どうやって?」と考えます。
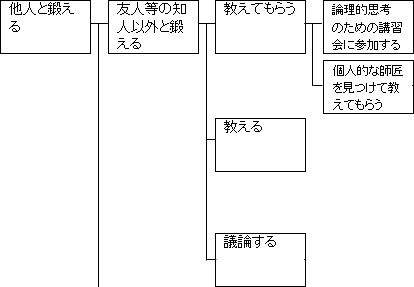
これは、「論理的思考のための講習会に参加する」ことで可能となります。
「講習会に参加する」以外にも、「知人以外に教えてもらう」方法があります。要は塾みたいな所がないか探して参加することになります。
他には、「個人的な師匠を見つけて教えてもらう」ことでも可能です。師匠という言葉が堅苦しくいなら、家庭教師と言ってもいいです。塾と家庭教師を比較しても分かる通り、家庭教師なら完全に自分に合せた指導を受けることができます。
図17.2.解決策の立案 画像クリックで拡大
次に、「教える」についてです。
上位階層を意識しつつ、「知人以外に教えて論理的思考力を鍛える」って「どうやって?」と考えます。
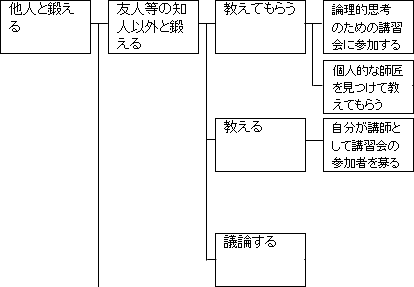
これは、「自分が講習会の講師として参加者を募る」ことで可能となります。
実際にこれを実行するのは難しそうですが、今は解決策を網羅して構想を出したいので、一応解決策の候補として挙げておきます。
図17.2.解決策の立案 画像クリックで拡大
「議論する」についてです。
「知人以外と議論して論理的思考力を鍛える」って「どうやって?」と考えます。
これは、「論理的思考のための勉強会に参加する」ことで可能となります。
「勉強会」は色々な種類がありますが、都合よく「論理的思考力を鍛える」ことに的を絞ったものがあるかは微妙な所です。しかし、ないわけではないでしょうから、一応候補として挙げておきます。
図17.2.解決策の立案 画像クリックで拡大
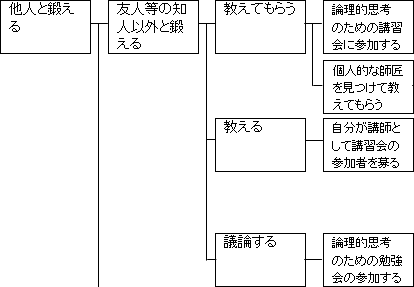
なお、「勉強会」と「講習会」の違いが曖昧に感じられるかもしれません。ここでは、次のように両者を別物と考えています。
「勉強会」は参加者が対等で、自分たちで議題等を設定して自主的に議論したり特定の内容を勉強して進めて行きます。
「講習会」では、講師がおり、その人を中心にして講義を受けたり、議論したりします。
要は、「勉強会」は参加者各自の自主性が前面に出るのに対して、「講習会」は講師のような指導者が引っ張って行ってくれます。
「勉強会」は、何をすればよいか分からない人が集まると碌に進まないかもしれませんが、「講習会」は最低限の質は保ちやすい傾向があります。
これ以上下位階層に掘り下げても、「どうやって?」という how? で問うと言うよりも、「何を?」という what? で問うようになってしまうので、ここらで一旦掘り下げは終えます。
実際に各命題を分解しようとしてみてください。「どうやってするのか?」というよりも、「何をするのか?」という問いの答えになり、実行するための作業や手順の話になっています。
図17.2.解決策の立案 画像クリックで拡大
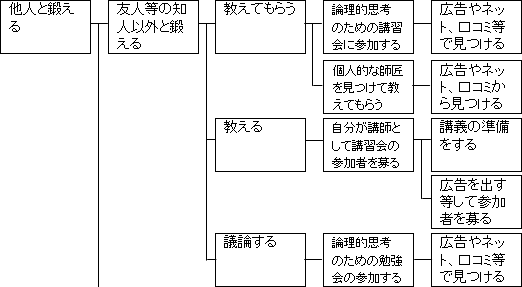
では、「友人等の知人と鍛える」場合に移ります。
ここでも、「教えてもらう」、「教える」、「議論する」に分解します。
基本的には「友人等の知人以外と鍛える」場合と、一部を除いて、ほとんど同じになります。
図17.2.解決策の立案 画像クリックで拡大
「教えてもらう」について考えます。
「知人に教えてもらって論理的思考力を鍛える」って「どうやって?」と考えます。
これは、「論理的思考の講習会に参加する」ことで可能となります。ただし、これは学校とが開講していないと実現は厳しそうです。
また、「師匠を見つけて教えてもらう」も、自分よりも優れた論理的思考力を持った人が必要なりますが、結構厳しい気がします。
「教える」について考えます。
「知人に教えて論理的思考力を鍛える」って「どうやって?」と考えます。
これは、「自分が講習会の講師として参加者を募る」ことで可能となります。「知人以外と鍛える」場合と同じです。
「議論する」について考えます。
「知人と議論して論理的思考力を鍛える」って「どうやって?」と考えます。
これは、「論理的思考のための勉強会を開くか参加する」ことで可能となります。
「知人以外と鍛える」場合と異なるのは、「勉強会を開く」ことも選択肢に入っている点です。実際に知人からの参加者があるかは別としても、知人に範囲を絞っているのなら、自主的な勉強会を開いて参加者を募るのも比較手容易だと考えられるからです。
図17.2.解決策の立案 画像クリックで拡大
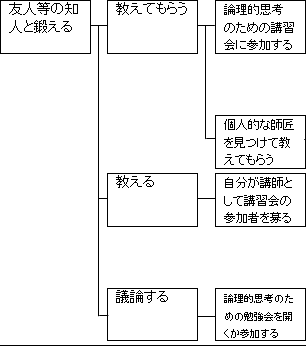
「知人以外と鍛える」場合と同様に、これ以上下位階層に掘り下げても、「どうやって?」という how? で問うというよりも、「何を?」という what? で問うようになってしまうので、ここらで一旦掘り下げは終えます。
実際に各命題を分解しようとしてみてください。「どうやってするのか?」というよりも、「何をするのか?」という問いの答えになり、実行するための作業や手順の話になっています。
図17.2.解決策の立案 画像クリックで拡大
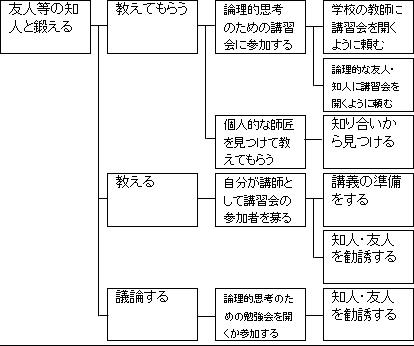
これで、how ツリーが完成しました。解決策の枠組み設定および構想出しが終わりました。
図17.2.解決策の立案 画像クリックで拡大
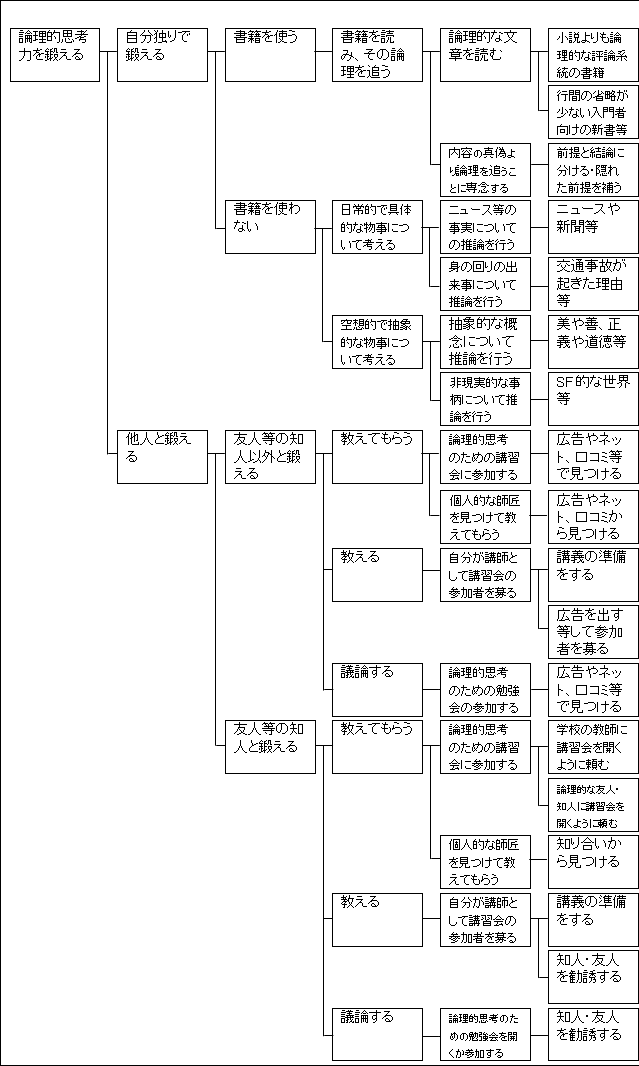
かなり大きな how ツリーになってしまい、おまけに途中で what ツリーに切り替わっている箇所がありますが、考えられる解決策を過不足なく考え出すことができました。
4 仮説設定
続いて、解決策の仮説設定をします。
今作った how ツリーは、具体的な解決策あるいは解決策の基本的方向性を表しています。この解決策を実行すると、課題が解決されるのか仮の説明たる仮説を考えます。
最初に、仮説を考える際の注意点を述べておきます。
how ツリーは、下位階層に下る程、各命題は具体的な手段になって行きます。
ですから、最下位階層ごとに仮説を設定するのではなく、ある程度の階層を一纏めにして仮説を設定します。
どこを一纏めにして1つの仮説と考えるかは、各場合によって異なるので、一概に絶対的な基準は言えません。が、それを踏まえた上で敢えて1つの指針を述べるならば、how ツリーを作るときに、how? ではなく、what? に切り替わっていると感じる場面で一纏めにすることを勧めます。
なぜならば、what ツリーが構成要素や構造を表すものだからです。
how ツリーを作っている最中に what ツリーが出て来るということは、そこから下の階層は、その範疇(カテゴリー)を構成する要素と考えられ、1つの纏まりと見なせるます。つまり、what ツリーによって現れた範疇(カテゴリー)は、how ツリーで具体化された手段を実行するために「何をしたらいいか」という「作業」となっているからと言えます。
今作った how ツリーで一纏めにすべき箇所を赤枠で囲ってみると、こうなります。
図17.3.解決策の仮説設定 画像クリックで拡大 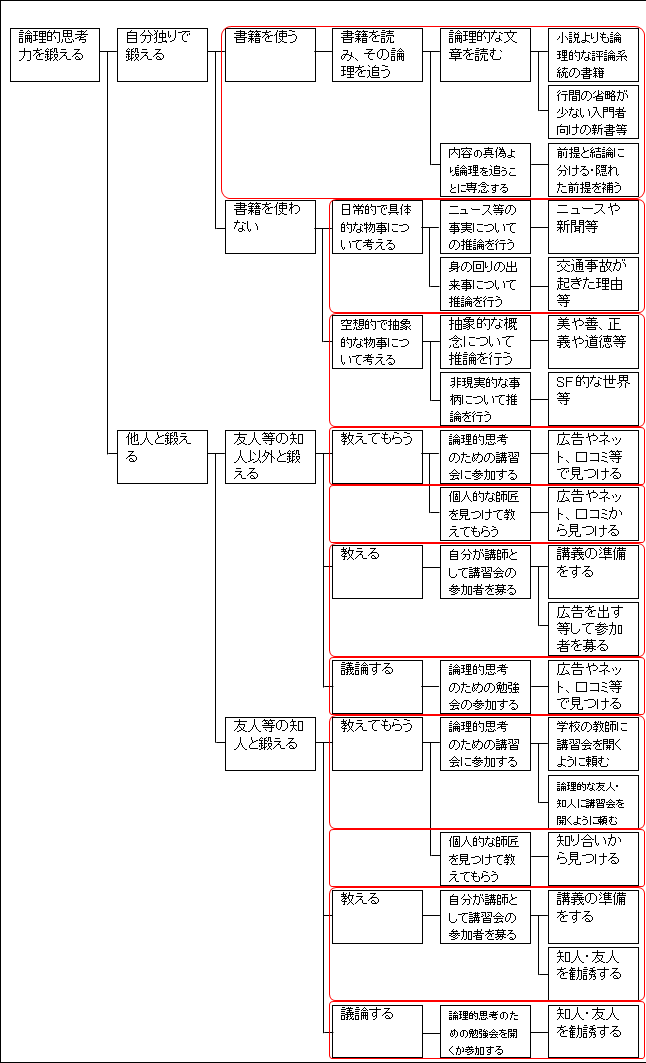
そして、各赤枠でまとめられた命題群の一番の上位階層を仮説として考えます。
「『上位階層』をすることで、『課題』が解決される」とすれば、仮説ができます。
これに基づいて、一番右の列に仮説を書き出してみます。仮説は、各階層を上手く繋げながら、最上位階層の課題の解決が達成されるかを考えます。
図17.3.解決策の仮説設定 画像クリックで拡大 
今回はこのように仮説として一纏めにしましたが、どれだけ大きく纏めて1つの仮説と考えるか、あるいは、小さく細かく1つの仮説と考えるかは、目的意識によって変わってきます。
予め大きい企画として動かすことが決まっているのなら、大きく一纏めとして仮説を考えてもいいです。
この場合、大きく一纏めした仮説を、小さな纏まりが構成するという全体と部分の関係になります。
逆に、そんなに大きい企画として動かすのでないなら、あまり大それた策を実行するのは難しいはずです。
その場合は、実効性の高い小さな纏まりの1つを仮説として選ばざるを得ません。
このように、どれだけの纏まりを1つの仮説として捉えるかは、状況によって異なることを理解しておいてください。
5 仮説検証と最適案の決定
how ツリーから複数の解決策の仮説が立てられました。次に、仮説の評価と検証をします。仮説の評価と検証は、実効性と実現可能性がどれほどのものかを考えることが大切になります(第14章 問題と解決 参照)。
もちろん、一度にすべての仮説の実効性と実現可能性を考えるのが最善です。
しかし、時間が無ければ、直感的に実効性と実現可能性が高そうに感じられる仮説を2、3個に絞って検証するだけでもいいです。
ただし、その際には、検討されていない仮説の方が適切であったという可能性が常にあることに注意してください。また、絞って検討した仮説がどうもダメそうなら、時間が無くても、他の仮説も検討してください。
さらに、実効性や実現可能性を細かく考えずに、大体の評価を大雑把に与えるだけでも構わない場合もあります。
その辺は、自分がどのような問題を扱っているのか、どこまで細かく詰めておきたいかによります。
臨機応変に対応してください。1.検証の基本と最適案の決定
さて、今回はすべての仮説の実効性と実現可能性の両方を評価・検証します。
最適案を決定する上での基準は、大きく分けて2つあります。
各解決策に「実効性」があるのか?、つまり、本当に課題を解決できるのか?
各解決策に「実現可能性」があるのか?、つまり、その解決策は実行することができるのか?
この2つが検証の柱となります。各解決策の仮説を「実効性」と「実現可能性」に分けて、どうなのかをそれぞれ考えてみましょう。
言うまでもありませんが、これも常に当てはまるわけではなく、こう考えれば一応は最低限考えるべき点は考えたことになる確率が高いといったものです。場合によっては、自分なりにもっと細かく考えたり、簡潔に考えたりする必要はあります。
本当に課題を解決できるのか? という「実効性」については、
課題をどの程度解決できるのかという「効果の程度」、
実際に解決できる確率はどれくらい高いのかという「解決の確率」、
解決策の効果が現れるまでに要する時間はどれくらいのかという「解決にかかる時間」、
この3つを主に考えるといいでしょう。
解決策は実行できるのか? という「実現可能性」については、
解決策を実行するのにかかる金額はいくらかという「費用」、
解決策を実行するのにどれだけ時間がかかるかという「期間」、
解決策を実行するのに必要な人材や物等といった「資源」、
この3つを主に考えるといいです。
(17.1)では、検証しようにも条件が緩すぎて何でもアリになるので、もう少し具体的な場合で考えます。
(17.1.1)を新たに見てください。太郎を取り巻く状況をより詳しく描かれています。
| (17.1)高校生の太郎は、学校の勉強を真面目にしており、試験の成績も良い。しかし、自分の頭で何かを考えることに苦手意識がある。例えば、教科書に載っているような事柄を問われれば、すぐに答えることができるが、1つに決まる答えがないような問題に対して、自分の意見を論理的に組み立てたり、説得的に述べることができない。そこで、太郎は、論理的思考力を鍛えたいと考えた。考えられる解決策を論理ツリーを用いて示せ。 (17.1.1)ただし、太郎の家は中流家庭であり、親は学校の勉強のための塾の費用は出してくれるが、それ以上のことについては金銭的な問題もあり、あまり協力的ではない。 また、太郎は、ある田舎の県立進学校に通っている。県内には熊本や博多、広島や岡山、京阪神、松山や新潟、名古屋や横浜、仙台や札幌のような大きな地方都市はない。 そして、家から都会の隣県に出るのに4時間程度かかる。新幹線を使えば、家から都会の隣県に出るまで2時間程度で出られる。 学校の教師の中で、論理的思考力等に長けていそうな教師は、部活の顧問をしており、暇ではなく、特別講義的な協力は仰げない。 |
(17.1.1)から、先程作った解決策の各仮説の「実効性」と「実現可能性」を考えると、こうなります。
図17.4.仮説検証 画像クリックで拡大
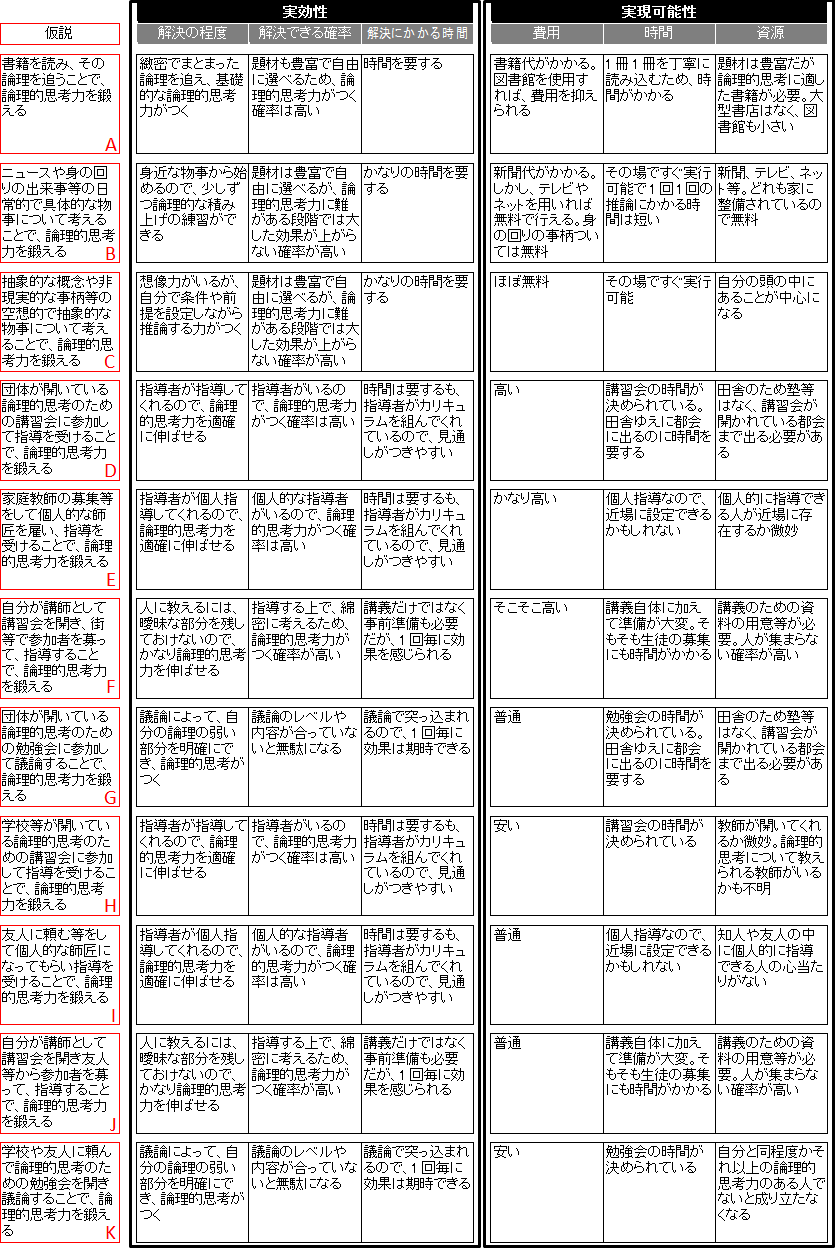
言うまでもありませんが、これは、(17.1.1)から私なりに仮説の「実効性」と「実現可能性」がどうなのかを考えた末に予測したものです。なので、これとまったく同じになる必要はありません。
あと、各仮説の右下には後で使うためにアルファベットの A ~ K を振っておきました。
仮説を検証するとき、時間や費用に余裕があれば、少しだけ実験的に試しに行ってみたりするといいでしょう。
そうすれば、頭で考えるだけよりも、解決策にどれくらいの実効性や実現可能性がありそうなのかが、具体的になります。人材や材料を実際に集めるのは難しいので、アンケート調査をする等でもいいでしょう。実際に企画を動かす場合には、こうした検証と効果測定を示しておくといいです。
さて、すべての解決策を同時に実行できるのなら、全部試してみるのがいいです。が、しかし、実際問題として、身体は1つですし、仲間がいてもその数は限られています。また、時間も有限です。どの解決策を実行に移すかを決めないといけません。
そして、何かしらを選択して決定するということは、選ばれるもの以外は捨てることを意味します。何を選び、何を捨てるべきか、これを考える必要があるので、優先順位をつける必要が出てきます。
そこで、各解決策の評価を比較して、優先順位をつけます。私はこのように順番をつけました。
もちろん、考え方は人それぞれあるので、私と全く同じようになる必要はありません。
図17.5.仮説の優先順位
| A | 1 | E | 8 | I | 4 |
| B | 2 | F | 10 | J | 9 |
| C | 2 | G | 6 | K | 11 |
| D | 7 | H | 5 |
こうすると、何かしら1つのみ実行する解決策を選ばなければならないとき、優先順位の高いものを選択すればよいことが分かります。
この優先順位によれば、解決策 A、つまり、「書籍を読み、その論理を追うことで、論理的思考力を鍛える」を選択することにります。
なお、複数の解決策を選択できる場合は、優先順位の高いものから順番に選べばいいと考えがちですが、注意が必要です。
単純に優先順位の高いものから複数選ぶだけでは効果的ではないかもしれません。
複数の解決策を選ぶ余裕はあっても、すべての解決策を選択することができる程ではないはずです。優先順位だけではなく、どの解決策の組み合わせが最も効果的で効率的に課題解決に繋がるかを考えて選ぶようにしてください。
なぜならば、単独では効果は高いが費用も高過ぎて優先順位が低かった解決策でも、他の解決策と共に実施できるなら、費用を抑えることができてきる場合等があるからです。
こうして最適な解決策を決定することができます。
2.決定マトリックス
今、実効性や実現可能性を言葉・文章で表しましたが、言葉だけで表していると、どれも甲乙付け難いと感じることがしばしばあります。先程の優先順位の付け方が本当に良いのかも不安になることもあるでしょう。そこで、どの解決策を選ぶべきかを決めるために、2つの考える方法を紹介しておきます。いずれも、マトリックスを使います。
マトリックスとは、英語の matrix がカタカナとして表されて日本語に定着したまものです。まぁ、だから言葉だけ聞いても何のことかイメージし難いかと思います。高校数学で行列を習っていたときは、説明が楽だったのですが、数学で使われる matrix は「行列」と訳されていました。
マトリックスを日本語に訳すならば、「母体」や「基盤」といった意味になります。
でも、翻訳というのは難しいもので、翻訳元(English)の言葉と翻訳先(日本語)の言葉がピッタリと一致するとは限らないんですね。
「母体」「基盤」といった日本語に訳される matrix ですが、もう少し詳しく言えば、「何かしらを生み出すもの・機能」という意味です。
「何かしら生み出すもの・機能」から「母体」や「基盤」といった名詞に日本語として意訳されたわけです。
しかし、残念ながらこの訳語はあまり定着せずに、マトリックスとカタカナで表記されることが多くなりました。
さて、何かしらを決定する際に使われるマトリックスを決定マトリックスと呼ぶます。マトリックスで考えることで、何が最適なのかが、視覚的に明らかになります。
先ず表を作りましょう。2軸を垂直に交わるように引きます。ちょうど xy 座標と同じような形になります。
図17.6.決定マトリックス
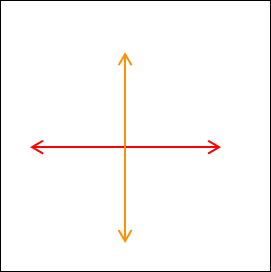
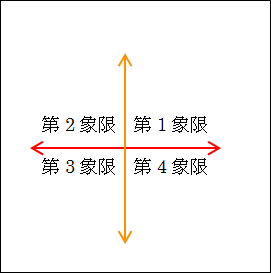
2軸によって、4つに区切られたわけですが、右上を第1象限と呼びます。
この第1象限を基準に反時計回りに、左上を第2象限、左下を第3象限、右下を第4象限と呼びます。
図17.6.決定マトリックス
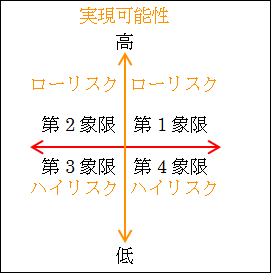
縦軸には「実現可能性」をとります。
上に行くほど実現可能性が高く、下に行くほど実現可能性が低いと考えます。
実現可能性が高いということは、成功する確率が高く失敗する確率が低いので、ローリスク low risk です。
逆に、実現可能性が低いということは、成功する確率は低く失敗する確率が高いので、ハイリスク high risk です。
図17.6.決定マトリックス
横軸には「実効性」をとります。
右に行くほど実効性が高く、左に行くほど実効性が低いと考えます。
実効性が高いということは、課題が解決される程度が高く得られる利益が大きいので、ハイリターン high return です。
逆に、実効性が低いということは、課題が解決される程度が低く得られる利益が小さいので、ローリターン low return です。
図17.6.決定マトリックス
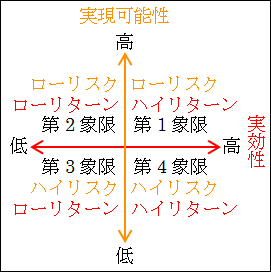
したがって、各象限の特徴が鮮明になります。
第1象限は、「実現可能性」も「実効性」も高く、ローリスク・ハイリターンだと分かります。この象限は。成功する確率も高い上に、見返りも大きいので、最善策と言えます。
第2象限は、「実現可能性」は高いが、「実効性」は低く、ローリスク・ローリターンだと分かります。この象限は、成功する確率は高いが、見返りは小さいので、安全策と言えます。
第3象限は、「実現可能性」も「実効性」も低く、ハイリスク・ローリターンだと分かります。この象限は、成功する確率も低い上に、見返りも小さいので、愚策と言えます。基本的にこの策はとることはしません。
第4象限は、「実現可能性」は低いが、「実効性」は高く、ハイリスク・ハイリターンだと分かります。この象限は、成功する確率は低いが、見返りは大きいので、強攻策と言えます。要は一か八かの博打的なものになります。
図17.6.決定マトリックス
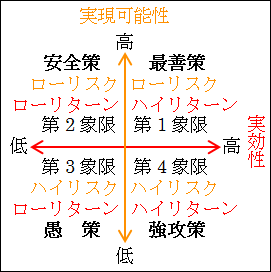
このマトリックスの中で、各解決策の仮説がどこに分類されるか考えてみます。
こうして整理してみると、どれが最善策で選択すべきかが明確になります。
第1象限に解決策が複数あれば、それらをよく比べればいいです。先程のすべての仮説を同時に色々考えるよりも比較が容易いはずです。
しかし、常に第1象限に分類されるものがあるとは限りません。むしろ、現実には、「実現可能性」も「実効性」も高い解決策がないことの方が多いかもしれません。その場合は次善の策を採用する必要があります。
そのとき、第2象限と第4象限にある解決策のいずれかを選ぶことになります。
第2象限は、「実現可能性」は高いが、「実効性」は低く、ローリスク・ローリターンの安全策です。
第4象限は、「実現可能性」は低いが、「実効性」は高く、ハイリスク・ハイリターンの強攻策です。
どちらを選ぶべきかは、自分次第です。
「ちょっとでも改善できればよし、まったく改善されないのが最悪だ」と考えたり、「失敗するくらいなら見返りは少なくてもいい」と考えるのならば安全策を選ぶことになるでしょう。
「ちょっと改善されても大して変わらないし、大きく改善されないと無意味だ」と考えたり、「失敗するかもしれないが、見返りが大きい方がよい」と考えるのならば、強攻策を選ぶことになるでしょう。
安全策を選ぶか、強攻策を選ぶかは、問題の性質や、自分が置かれた状況などで判断が分かれます。
解決策の仮説 A ~ K をマトリックスに書き込んでみましょう。
図17.7.決定マトリックスの例
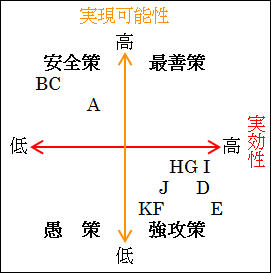
こうやって各解決策を「実効性」と「実現可能性」の中でどのような位置にあるかを確認してみると、何を選択すべきかが分かりやすくなります。
安全策で行くなら、解決策 A、B、C のどれかを採るべきです。
強攻策で行くなら、解決策 D ~ K のどれかを採るべきです。
さらには、安全策といっても「実効性」が低すぎたら意味がないと考えるなら、解決策 A になります。
強攻策といっても、「実現可能性」が低い割には「実効性」も大して高くない解決策 F、G、H、J、K は得策とは言えそうにないのが分かります。だとすると、どこまでリスクを取るのか、リターンをどれほど求めるのかによって、解決策 D、E、I のどれかを選択することになります。
このように、決定マトリックスを利用することで、言葉だけでは見え難かった各解決策の相対的な関係が理解しやすくなります。
3.数値化
この決定マトリックスの他に、もう1つのマトリックスを使った方法が、数値化して考えるやり方です。例えば、通知表を思い浮かべてみてください。皆さんの成績は、各教科ごとに、5段階または10段階で評価されているはずです。そして、それを合計して平均して、学年の順位が決まっているはずです。それと似たようなことをして、解決策の優先順位を決めます。
まず、数値化する要素・項目を決めます。
大雑把に「実効性」と「実現可能性」の2項目だけを考えても、仮説の数が多い場合には微妙な順位付けができないので、余り意味がありません。そこそこ詳しく項目を分けてやる必要があります。
そこで今回は、先程検討したように、6つの項目を設けます。
「実効性」を「効果の程度」、「解決の確率」、「解決にかかる時間」、この3つの項目に分けます。
「実現可能性」を「費用」、「期間」、「資源」、この3つの項目に分けます。
これが数値化して評価すべき項目の選定になります。
そして、各項目を数値化します。
今回は、5段階で評価します。数字が大きいほど評価が高く、数字が小さいほど評価が低いことを示します。1~5の値の中で、どういう場合ならば、どの値(得点)になるのかを決めます。
なお、もっと細かい違いに注目して分けたいなら、10段階評価にすることもできます。逆に、細かい微妙な違いは判断が難しいので大雑把に捉えるのにすませたいのなら、3段階評価にすることもできます。解決策の候補の数と、考えている対象の性質に応じて、自分で使い分けてください。
今回は、具体的には、次のように設定してみます。
図17.8.仮説の数値化 画像クリックで拡大

この6つの項目が同等に重要なら、そのまま数字をつけて合計得点を出せばいいのですが、必ずしも同等は限りません。項目によって重要性が異なることがあります。
重要性が高い項目は、重視したいところです。
これは、皆さんも、入試科目を思い浮かべてください。英語や数学は配点が高く、理科や社会の配点は低く設定されていることが多いかと思います。英語は200点満点なのに、物理は100点満点だったりすることがあります。英語が重視されている表れです。
2科目が70%と80%との得点率だとすると、英語が重視されることで、合計点が変わってきます。
まず、英語も物理も100点満点で重要性が同等の場合を確認しておきます。
英語の得点率70%で物理の得点率80%の場合、合計点は70+80=150点となり、75%となります。
英語の得点率80%で物理の得点率70%の場合、合計点は70+80=150点となり、75%となります。
英語と物理の得点率のどちらが70%と80%であろうとも、合計点は同じになり、優劣は生じません。
それでは、英語が200点満点で、物理が100点満点とし、英語に重要性があるという配点になっているとどうなるでしょうか。
英語の得点率70%で物理の得点率80%の場合、合計点は140+80=220点となり、73.333…%となります。
英語の得点率80%で物理の得点率70%の場合、合計点は160+70=230点となり、76.666…%ととなります。
そうすると、英語の得点率が80%のときの方が、合計点が高くなります。約3.3%の違いが生じています。
このように、重要性が高い項目は、他の項目よりも得点が高いときに、より総合点が高くなるように傾斜がかかるように考えてやることが日常的に行われいます。
重要性が高い項目の評価が、それより重要性が劣る評価と同じ扱いでは、総合的な判断に相応しくないと言えるからです。重要性が高い項目は、その重要性に応じて、評価に占める割合を高くして考えることが求められます。
こうした、各項目の重要性に応じて、総合評価に与える影響度に変えることを比重をつけると言います。
英語では weight と呼ばれます。今は日本語でも、ウェイトを付けて考えるとか言う場合もありますね。
重要性が高ければ、影響度を大きくします。逆に、重要性が低ければ、影響度を小さくします。
比重は、合計で1となるように設定します。
百分率あるいはパーセントで考えると100%で考えることになります。別に100%の中の何%なのかという考えでもいいですが、今回は全部で1になるようにして、影響度を小数で考えるようにしています。
このように、比重は、合計得点の中で、どれだけの重みがあるかを表しています。比重の付け方で、合計点は変わります。
各項目が同じ程度に重要な場合なら、1つの項目の割合は、1/総項目数となります。
今回ならば、数値化して評価する項目が6個あるので、1÷6≒0.1666…になります。百分率・パーセントで表せば16.666…%、分数なら1/6です。
これは比重を考えるときに参考になります。
すべての場合が同じ程度に重要な場合に影響度がどの程度あるのかを示しています。したがって、重要性が高いのなら、この1/総項目数の値よりも高いことが多いです。逆に、重要性が低いのならmこの1/総項目数の値よりも低いことが多くなります。
さて、この数字を項目の重要性に応じて、変えます。今回は、私なりにこのように設定してみました。
図17.8.仮説の数値化 画像クリックで拡大

「実効性」全体で0.4(40%)、「実現可能性」全体で0.6(60%)という割合です。
これは、「実効性」よりも「実行可能性」の方がやや重要と考えたからです。高校生段階ということもあり、「実効性」が少しでもあるのなら、「実現可能性」を重視すべきだからと考えています。
言ってみれば、安全策に傾くような比重の付け方です。
これで後は、平均点あるいは合計点を出して、その得点の高い順に優先順位をつければいいです。
図17.9.仮説の数値化と検証 画像クリックで拡大
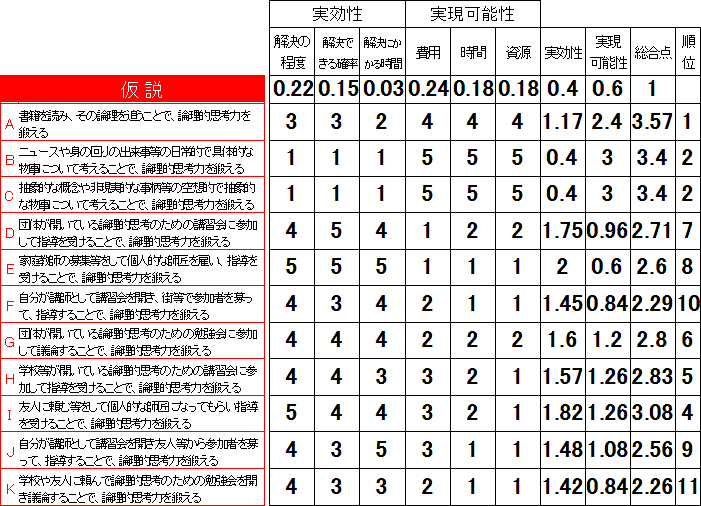
こうすることで、「実効性」と「実現可能性」の両方を考慮した優先順位が数字として表せるので、どの解決策を選択すればいいのかが明確になります。
ちなみに、「実効性」と「実現可能性」の項目は、各項目の平均です。
つまり、「実効性」は、「解決の程度」「解決の確率」「解決にかかる時間」の3つの項目の平均となっています。
「実現可能性」は、「費用」「時間(期間)」「資源」の3つの項目の平均となっています。
もちろん、各項目の比重を考慮した値です。
解決策の候補が11個もあり、評価項目が6個もあるので、各評価項目を個別に検討していると、各解決策のどこが良いのか、どこに弱点があるのかが分かり難いです。そこで、「実効性」と「実現可能性」という2つの大きな枠の中で理解することで、11個の解決策の候補の特徴を大掴みできます。
他にも、この表の利用法があります。
比重を加味した「実効性」と「実現可能性」の得点の平均は、それぞれ1.2と1.8です。0.4×3=1.2、0.6×3=1.8だからです。
この平均値を上回っている数字を黄色で塗りつぶしてみます。
黄色で塗られた箇所は平均以上で、白塗のままは平均以下ということを示しています。
図17.10.仮説の数値化と検証2 画像クリックで拡大
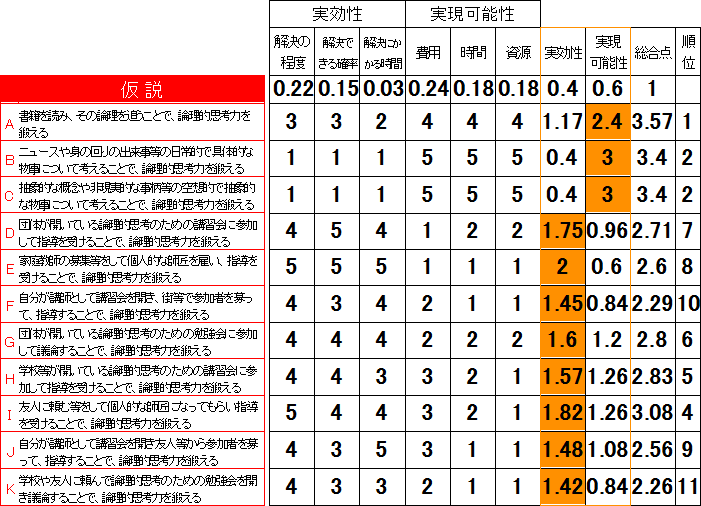
ここで、先程の「実効性」と「実現可能性」を2軸とした決定マトリックスを思い出してください。軸がそれぞれ平均値になっています。
「実効性」において、平均値1.2以上なら軸の右側に置かれ、平均値以下なら軸の左側に置かれます。
「実現可能性」において、平均値1.8以上なら軸の上側に置かれ、平均値以下なら軸の下側に置かれます。
そうやって、各仮説を配置すると、決定マトリックスと同じような配置になります。確認してください。
図17.7.決定マトリックスの例

このように、図にしたり、表にしたりすることで、解決策の各仮説の特徴を捉えて、自分がどのような目的で解決策を選択するのかを考えながら、最適案を選んでください。
最後に数値で仮説の優先順位を決める方法について、気を付けなければならないことがあります。この数値化して考えるのは、実際にはかなり難しいからです。
まず、各項目を1~5の数字で評価する基準を適切に設定する必要があります。
これは各項目と仮説の内容をしっかりと理解していないと上手く設定できません。
また、そもそも内容の性質上、数字にして評価することが難しい場合があります。
項目によっては、数値化することが困難なことは多いです。「幸せ」とか数値化しようにも非常に難しいかと思います。こういったものが仮説の評価の対象になると、数値化できない場合もあります。
さらに、各項目の比重のつけ方も非常に難しいです。
各項目の重要性の違いをしっかりと認識し、なおかつ、適切な割合を設定しないといけません。しかし、その重要性の違いをどうやって適切に判断するのか、比重のつけ方が適切なのかという疑問や問題は常につきまとうことになります。
こうしたことを踏まえると、自分がどのように考えるか、つまり、解釈するか、ということにかなり左右されることが分かります。数字で表されると、ついつい客観的に考えているつもりになりがちですが、実はかなり主観的になっている危険があります。
ですから、数値化するのに慣れるまでは、安易に使わずに、色々と考えた上で解決策を選択し、数字をどのよに割り振れば妥当なのかということを試行錯誤して経験を積んでいくことをおすすめします。そして、数値化された結果の数字自体がどのような意味を持っているのかをしっかりと考えて理解しておく必要があります。
これは自分で仮説を考えるときだけではなく、文章を読み解く際にも大切になります。数字を見ても鵜呑みにするのではなく、どういう意味で使っているのか、本当に適切に数値化されているのか、といったことを常に考えながら批判的に読む必要があります。気を付けてください。
以上で、仮説を検証して最適案を決定することができました。
さて、後は、選択した解決策を実行するには何をすればいいのかについて情報を集めて計画を立てればいいだけです。
どれくらいの時間や費用が必要なのか。人手は足りているか。新たな人材が必要なのか。必要な物は何か、といったことを具体的にしていきます。
そして、実行するための手順等を練って、どこで見直しを適宜入れるか等を考えて実行計画を作ればいいです。
計画はできるだけ綿密に立てておくべきですが、完璧主義になり過ぎても仕方ありません。
必要な情報が最初からそろうことの方が少ないです。おまけに、実際にやってみると、思ったように進まなかったり、予期せぬことが起きるものです。その際には、臨機応変に計画を修正したり、出来事に上手く対処するようにしていかないといけません。
もちろん、計画があまりにも具体的ではなく、大まか過ぎていいと言っているわけではありません。そんな計画では、実際に何をするのかが不明瞭で、場当たり的になりやすく、効率が悪くなります。
ただ、計画通りに行くことの方が少ないので、計画をどこまでも細かく作り込み過ぎて、さらには未だ足りないと考えて計画を練ることに集中しても、完璧にならないことの方が多く、計画を立てることに時間をかけ過ぎていては、何時まで経っても解決策の実行に移れず、したがって問題も解決できません。
計画を立てる目的は、問題を解決するためであるので、計画を立てること自体に囚われ過ぎないでください。計画は目的を達成する手段です。手段を目的化 しないでください。論理ツリーを作るときにも注意しましたが、実行計画を立てる段階でも、杜撰になり過ぎず、完璧に拘ら理過ぎず、バランス感覚を持って、目的達成志向を貫くことが大切です。
6 まとめ
長くなりましたが、論理ツリーを使って、問題を課題化した後にどのように解決すればいいかを考え出す方法について説明しました。
「発生型」の問題では why ツリーで、本質的な原因を分析しましたが、次の章で説明する「設定型」の問題や「創造型」の問題にしろ、更に後で説明する「構造型」の問題、「現象型」の問題にしろ、現状を分析して何が本質的な課題なのかが分かった後は、解決策を考える段階に移ります。
課題解決策を考え出すために、論理ツリーを実際に作るとき、まず課題が解決された状態とはどういった状態なのかを大雑把に、しかし、しっかりと捉えることから始めました。それを基にして、制約条件や前提条件を確認して、枠組みを使いながら MECE に分解して、how ツリーを作りました。「どうやって?」と考えながら、どんどん分解していきます。
解決策がある程度具体的になったら、各解決策の仮説を組み立てます。そして、各解決策の仮説の実効性や実現可能性を検討してみて、どの解決策を実行するのかを選択しました。
こうして、課題を解決するために最も効果的で効率的な解決策を選ぶことができた後は、実行手順や必要な資源等を細かく計画していけばいいことになります。
これで論理ツリーの使い方の説明が終わりました。第13章からの論理ツリーの話をザックリとまとめもしておきましょう。
構造や概念を整理するための what ツリー、原因を特定するための why ツリー、解決策を考え出すための how ツリーと目的によって微妙な違いがありました。
what ツリーは「何が?」、
why ツリーは「なぜ?」、
how ツリーは「どうやって?」
と分解の仕方が異なりましたが、MECE に分解する点では共通していました。
それ故に、具体的な物事から積み上げて抽象化していくボトムアップ方式もありますが、論理ツリーと相性が良いのは、最も一般的で抽象的な最上位命題から分解していくトップダウン方式でした。
さらに、後で登場する因果関係図や論理ピラミッドでもそうですが、特に論理ツリーは、枠組み framework で考えることも有効でした。
枠組みは、対象をどのように見るか、どのような切り口で切るかといった視点を提供してくれます。これを勉強すると、物事を色々な視点から考えられるようになります。
しかし、枠組みに頼り過ぎて安易に当てはめては意味がないことにも触れました。枠組みを単なる知識として使うのではなく、実際に自分でその論理を追いながら使って経験することが重要性です。そして、何より自分で枠組みを作ってみることが大切になります。
以上で、論理ツリーについて終わります。次は、論理ツリー、特に how ツリーとの関係する「設定型」の問題と「創造型」の問題について軽く説明します。
前頁:第16章 論理ツリー ― why ツリー―
ページトップへ:第17章 論理ツリー ― how ツリー―
次頁:第18章 設定型の問題と創造型の問題