前頁 |▼| 次頁
第26章 定性的研究と定量的研究
学問と科学が、信頼するに値するものとして考えられる理由は、厳密な科学的方法に則っているからです。そして、科学的方法とは、観察―仮説形成―仮説検証という手順あるいは手続きです。では、科学的方法の大枠が理解できたところで、具体的に研究はどのように行われるのでしょうか。これについて学びます。
研究は、観察対象のどこに注目し、どのように表現するかで、定性的研究と定量的研究に分けられます。科学的方法に則っとりながら、この2つの研究が相互に補い合いながら、学問と科学を発展させています。
| 目次 |
| 1 概略 2 定性的研究 3 定量的研究 4 定性と定量の役割 5 まとめ テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 概略
前章で科学的方法について説明しました。科学の研究が、どのような手順によって進められるかを学びました。科学的方法は各専門分野によって手順や決まり事に細かい違いはありますが、大きく見れば、観察して仮説を形成して検証してという循環は共通しています。
そこで、科学的方法の理解をより深めるために、研究の対象および内容の面からその様式の違いを見てみます。
科学的方法は、研究対象をどのように観察して表現するかによって大きく2つに分けることができます。
まず、対象の1つあるいはごく少数に絞って、その対象をひたすら詳細に調査する場合が考えられます。
次に、対象が大量に存在し、それらをひとまとめてにして1つの対象として調査する場合が考えられます。
この2つのそれぞれが、定性的研究と定量的研究です。
定性的研究とは、対象の性質に注目して分析する研究です。
英語では、qualitative research と言います。qualitative は、「質」を意味する quality の形容詞形なので、「質」に関する研究だと分かります。「性質」という言葉があるように、「性」も「質」も似たような意味で、どちらも本質や性質といったことを意味します。
定性的研究で扱われるデータは、質的データと呼ばれます。
インタビューやアンケート調査、観察結果、文章、そして歴史的史料や遺跡等が、この質的データにあたります。どれも質的データの内容が重要になります。
ですから、研究内容は、言葉で書き表して記述することになります。
定量的研究とは、対象を数字や数量として分析する研究です。
英語では、quantitative research と言います。quantitative は、「量」を意味する quantitiy の形容詞形なので、「量」に関する研究だと分かります。
定量的研究で扱われるデータは、量的データと呼ばれます。
数字や統計などが、この量的データにあたります。対象1つ1つの個別の内容よりも、全体を数字に落とし込んで処理することが重要になります。
ですから、研究内容は、数字や数式で表すことになります。
以上のように、科学的方法に則って研究するとき、着眼点と表現方法によって定性的研究と定量的研究に分類できることが分かりました。
これから話す内容は次のようにまとめられます。この表が意味する内容を理解できれば、十分です。
| 定性的研究 | 定量的研究 | |
| 着眼点 | 対象の性質 | 数値や数量 |
| 表現法 | 記述 言葉による説明 | 数学・統計 数式・論理式による説明 |
| データ | 質的データ | 量的データ |
| インタビュー アンケート調査 観察結果 文章 歴史的史料 遺跡 | 実験 大量の観察結果 統計資料 | |
| 目的 | 対象の包括的説明 仮説・モデルの形成 | 対象の因果関係の証明 仮説・モデルの検証 |
| 方法 | データから概念的・操作的定義の抽出 記述的推論 因果的推論 | 大量のデータの分析 変数と変数値を用いた分析 再現可能性の確認 |
| 研究例 | 事例研究 少数事例の比較研究 | 理論研究 多数事例の比較研究 |
| 欠点 | 仮説検証(再現可能性の確認)が困難 | 数値化・数量化できない対象は分析不可 |
なお、定性的研究と定量的研究は、どちら一方が優れているということはありません。たまに両者を対立させて、優劣を語る人が見受けられるので一応注意しておきたいと思います。
どちらの研究も科学では必要であり重要です。 定性的であることと定量的であることは対立しません。どちらにも長所があり欠点があり、相互に補い合う関係です。
それに、定量的研究で数式や数字によって表す場合でも、対象の分析や構造の把握は定性的研究のように言葉で記述することから始まることが多いです。
また、数式や数字で表されたことも、それだけでは何を意味しているのか理解できないので、定性的研究のように言葉での記述をして説明することになることがほとんどです。
このように、定性的研究と定量的研究を明確に完全に区別することはできません。
要は、定性的研究と定量的研究の適宜いずれかを用いて研究すればいいのであって、ある研究の中でどちらが主になろうとも、科学的方法の手続きに則っており、基本的な推論の論理によって導かれていることが重要になります。
それでは続いて、定性的研究と定量的研究の特徴を順番に少し詳しく見ることにします。
2 定性的研究
まず、定性的研究の特徴から見て行きましょう。
研究対象は、1つの事例、あるいは少数の事例のことがほとんどです。
定性的研究は、観察した対象の本質や特徴・性質を言葉によって表現します。
対象となる物質や現象が、どのような特徴があるのか、どうなしてそうなっているのか、といったことを丁寧に詳しく表現します。
こうした言葉による表現を記述と言います。
対象を分析して、推論し記述することについて見ます。
観察した対象は、複雑怪奇です。そのまま理解できればいいのですが、それは人間の認識能力を大きく上回ることが多いです。
そこで、対象を理解できるように、その本質や特徴を記述します。
記述することで、「Aとは~である」、「Aには…という特徴がある」といった具合に言葉で対象を明確にすることを目指します。
私達は言葉で考えるので、理解できるように対象を言葉で表してやる必要があるからです。
このとき、観察して得られたことを根拠たる前提として、推論することになります。今まで勉強して来た論理的思考が活躍します。
図26.1.定性的研究と記述 画像クリックで拡大 
対象を理解するために、本質的でない要素は、捨象(捨てて)して抽象化します。
図26.1.定性的研究と記述 画像クリックで拡大 
抽象化するわけですから、対象を理解するのに重要で必要な本質や特徴に注目して抜き出すことになります。
図26.1.定性的研究と記述 画像クリックで拡大 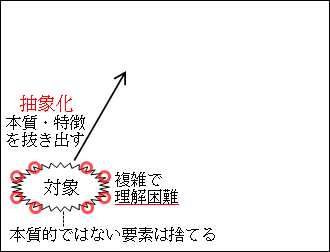
つまり、対象は個別的で具体的なものから、一般的で抽象的な概念になります。
こうして、抽象的な概念的定義が形成されます。
概念的定義が、事物の本質や特徴を捉えて、明確に言語化した定義なので、複雑な対象が理解できる形に整理できています。
このとき、「Aって何?」って訊かれたら、「Aは、~だよ」とズバッと答えることができます。
図26.1.定性的研究と記述 画像クリックで拡大 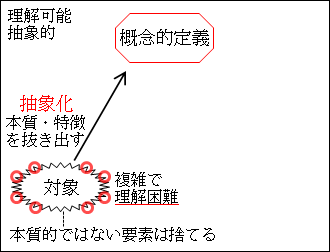
しかし、概念的定義には問題があります。
概念的定義は、複雑な対象を言葉で表していますが、まったく同じということにはなりません。
図を見ても分かる通り、複雑な対象は、ギザギザの複雑な形をしています。これに対して、概念的定義は、本質や特徴が抜出されて八角形という分かり易い形に整理されています。概念的定義は、複雑な対象を表していますが、細かい部分は無視しており、まったくそのままそっくりに同じだということにはなっていません。
また、複雑な対象が抽象化されて理解できるようになったかわりに、概念的定義を観察することが難しくなります。
対象は、実際に事物として存在しており、「これが対象だ」と指し示すことができます。これに対して、概念的定義は、言葉です。言葉は私達の思考の源ですが、どうしても曖昧さが残ります。したがって、抽象的な概念的定義が何を表しているかが少し不明瞭になっています。したがって、何を実際に観察すればいいのかが曖昧になってしまいます。
図26.1.定性的研究と記述 画像クリックで拡大 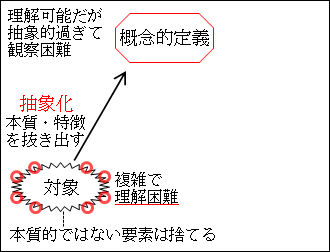
ですから、概念的定義を観察するために、操作的定義として具体化してやればいいです。
そこで、概念的定義に抽象化されていた本質や特徴に再度注目します。
図26.1.定性的研究と記述 画像クリックで拡大 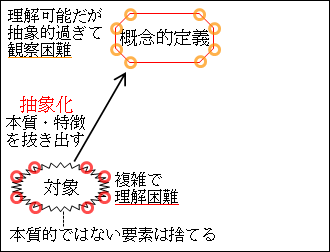
概念的定義として抽象化された本質や特徴を具体化すれば、操作的定義となります。
操作的定義は、直接測定できない対象を測定可能な形式に変形した定義であり、抽象的な概念的定義を一段階具体化したものです。
このように、操作的定義は、概念的定義を構成する本質的な要素や性質だと考えることができます。
図26.1.定性的研究と記述 画像クリックで拡大 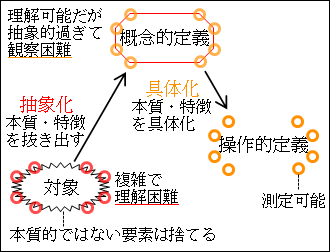
以上のように、観察した対象を記述することができます。
つまり、抽象的な概念的定義と、それを具体化した操作的定義を記述していけば、対象を明確に言葉で表現することができます。
これで、対象がどのようなものなのかを理解できます。
そして、こうした複雑な対象を理解可能な形に整理して、その本質や特徴を明確に表現することを記述的推論と言います。
対象の大枠や本質の理解ができたら、因果関係の有無を考えます。
やはり、科学的な研究では、観察対象が何故、あるいは、どうやって起きるのか、ということに興味関心が向きやすいです。研究対象によっては因果関係を見つける必要はない場合もあり、必ずしもすべての研究が因果関係について考察するとは限りませんが、多くの場合、因果関係へ興味が向かうものです。
因果関係への興味、つまり、何が原因となって、このような結果が引き起こされているのだろうか。こういった疑問についての推論を行います。そうした因果関係についての推論を因果的推論と言います。
そして、論理的思考を用いて推論するからには、記述的推論にしろ因果的推論にしろ、根拠たる前提は、客観的で確固とした事実です。これがデータになります。
このデータから概念的定義と操作的定義を読み取ります。
ですから、論理ピラミッドで論理構造を表すと、概念的定義が最上位命題になり、その下の階層に操作的定義、さらにその下にデータが置かれることになります。
図26.2.概念的・操作的定義・データと論理構造 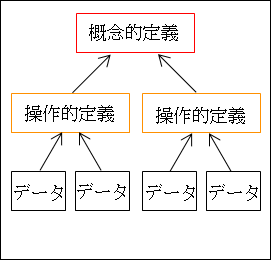
そして、このデータは様々です。
インタビューやアンケート調査といった聴き取り調査。歴史的史料や議事録等の文章。物質や現象の観察結果や発掘された遺跡などです。
どれも個別の具体的な物事です。
図26.2.概念的・操作的定義・データと論理構造 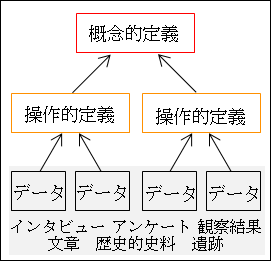
そして、個別的で具体的であり、客観的で確固とした物事・事実がデータとなるので、データはデータの意味内容や性質が重要になります。したがって、こうした内容が重視されたデータを質的データと呼びます。
これから分かることは、定性的研究において、一度の研究での観察の対象となる数が少なくなってしまうことです。
概念的定義を導くとき、個別的で具体的な物事を丁寧に観察して、対象の本質とは一体何なのか、何故そうなっているのか、といったことを分析しています。
したがって、何千何万といった個別的で具体的な事例を丁寧に調べることは時間の関係から難しいです。
そのため、定性的研究は、事例研究や少数事例の比較研究といったものになります。
1つの事例について研究したり、少数の事例についての研究は、いわゆるケース・スタディあるいは事例研究と言われます。ある事柄についての典型的な事例を考察するものです。
または、考察した少数の対象を比べて差異や共通点について研究する場合もあります。こうした研究は、少数事例の比較研究です。
以上説明したように、1つの仮説、あるいは、モデルが出来上がります。
つまり、疑問に思ったこと、分からなかったことに対する合理的な説明がなされたり、現実を再現することができたことになります。
そして、この定性的手研究による仮説は、個別的で具体的な事例だけではありますが、それについての包括的な説明にはなっています。
ですから、定性的研究だけで導かれた仮説やモデルは、客観的で確固とした事実から推論されていれば、これだけでかなりの説得力があります。
しかし、それでも仮説は仮説です。検証なしに、仮説が本当に事実と合致した説明であり正しいのかは分かりません。正しいかもしれませんし、間違っているかもしれません。
したがって、仮説であるからには、実際に事実と合致しているかを検証しないといけません。
この検証を行うときに、定量的研究の出番となります。
3 定量的研究
それでは、仮説検証にも役立つ定量的研究について見て行きましょう。
定量的研究では、観察した対象を数字や数量として分析します。
つまり、観察対象を数式で表したり、統計の数字で表したりします。数学的・統計学的な方法が多く用いられます。
また、定量的研究は、一般的で抽象的な説明を目指すことが多いです。
定性的研究では、観察対象の本質や特徴・性質を包括的に説明する記述をしました。しかし、それはあくまで個別的で具体的な1つあるいは少数の事例を考察したものです。その個別的で具体的な事例を包括的に説明したものが、その実際に観察された対象以外の類似した事例に対して当てはまるか否かは不明です。一般的で抽象的な理論、つまり、法則的で統一的な説明として、事実と合致しており正しいかどうかは分かりません。
そこで、個別的で具体的な事例の包括的な説明としての仮説を、数学的・統計学的な方法によって大量に検証するのが定量的研究になります。大量の事例を調べることになるので、一般性が高まることになります。
定量的研究に入る前に、定性的研究の問題点を確認しておきます。1.再現可能性
まず、確認しておきたいのですが、個別的で具体的な事例は基本的に1回限りです。まったく同じ事例は、もう二度と起きません。
こうした1回限りで再現ができないことを、再現不可能性 irreproduciblity と言います。再現不可能性は一回性とも言われたりすることがあります。
そして、再現不可能性があるので、まったく同じ事例は存在しないにもかかわらず、ある個別的で具体的な事例から導いた一般的で抽象的な仮説やモデルが、類似した事例に対しても同じように理解できると考えていることになります。つまり、まったく同じ事例は二度と起きないのに、類似した事例で、同じ仮説やモデルが成り立つと考えていることになります。
これが問題なのです。
ですから、ある1つの個別的で具体的な事例から導いた一般的で抽象的な仮説やモデルが、他の類似の事例でも成り立つことを論理的に確認します。
そこで、論理的思考の特徴を思い出してもらいたいのですが、正しい前提から正しく推論されれば、結論も正しくなるという性質です(第1章 論理的であるとは参照)。そして、同じ前提から、同じ推論をすれば、結論も同じになるという性質もあります。
一般的で抽象的な仮説やモデルは、個別的で具体的な事例の特徴や性質を抽出して、これを根拠たる前提として作り出しました。
再現不可能性のために、まったく同じ事例は見つけ出せなくとも、仮説の前提となる特徴や性質を持った事例ならば、見つかることはあります。まったく同じ事例ではないが、同じ特徴や性質を持った事例は、類似の事例と考えることができます。
したがって、もし同じ特徴や性質を持った類似の事例ならば、仮説と同じ前提から、仮説と同じ推論をすることができます。そうすると、結論も必然的に同じになります。
これで、一般的で抽象的な仮説やモデルは、ある少数の個別的で具体的な事例から形成されたものですが、他の類似の事例にも当てはまるものだと考えることができます。
したがって、ある1つの事例において、個別的で具体的な事例の本質と特徴を上手く抽象化して仮説やモデルが作れていれば、類似した事例がどのような結果になるのかを予測できることになります。
こうしたモデルによって同じ条件を整えれば同じ結果が得られることを、再現可能性 reproducibility があると言います。
この再現可能性があることが確認できれば、その仮説やモデルは証明されたと言えます。
よって、再現可能性を確認するために、類似した事例を大量に集めて、同じ条件ならば同じ結果を得られることを観察することになります。
大量の類似の事例を観察するので、1つ1つを細かく見て行く定性的研究ではなく、大量の事例を扱うのに適した定量的研究の出番となります。
ここで、さらに疑問に思った人がいるかもしれません。論理的に正しいのにもかかわらず、わざわざ大量の事例で再現可能性を確認するのは何故なんだと。
それは論理的な構成が正しかったとしても、見落としている事実や前提等が常に存在している可能性があり、それに気付いていないかもしれないからです。
仮説として「この前提からは、このように結論が導ける」と考えたとします。しかし、ある前提を見落としていて、それを考慮すると、最初に導いた結論は導けない場合が多々あります。
友達と議論しているときも、見落としていた前提や事実を指摘されて、自分の論が否定されたことがあるはずです。これは科学的に研究する場合も起こり得ます。
ですから、類似した事例について大量のデータを調べて、同じ条件ならば同じ結果になることを確かめて再現可能性があることを実際に確認しておくことが大切になります。
仮説やモデルは、検証なしにその正しさは証明されないので、頭の中だけではなく、事実と合致していることを実際に確かめないといけないわけです。
もし、これで思ったような結果が得られなければ、現実が間違っているか、仮説やモデルが間違っているかのどちらかです。
現に起きていることを否定しては宗教になってしまうので、必然的に仮説やモデルが誤りになります。その場合は、何か前提に見落としがあることや推論方法に問題があることを潔く認めて、仮説を修正しないといけません。
このように、頭で考えただけではなく、実際に現実に起きていることと合致して再現可能性を確認したいから、大量の類似した事例をデータとして観察することが必要なのです。2.定量的研究の分析方法
さて、再現可能性を確認するために、定量的研究が何をしているのかを見てみましょう。
まず、大量の事例を観察するために、データたる事例を集めます。さて、大量のデータを取るとは、どういうことなのでしょうか。考えてみます。
大量の事例(データ)の収集
大量のデータとして集められる1つ1つの事例は、個別的で具体的な事例です。
ただ闇雲に何でもかんでも集めるのではなく、抽象的な概念的定義に当てはまる事例を集めることになります。
さらに具体的には、操作的定義を調べることになります。
図26.3.大量のデータの収集 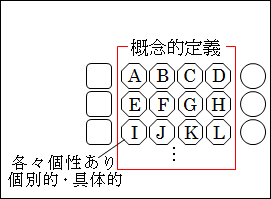
数字に置き換える
なお、このとき、1つ1つの個別的で具体的な事例の本質的要素以外は無視され、したがって、それぞれの事例の個性は失われます。
そして、1つ1つの個別的で具体的な事例は、一般的で抽象的な概念的定義が規定する本質や特徴を持つものとして一纏めにされ、数字に置き換えられます。
図26.3.大量のデータの収集 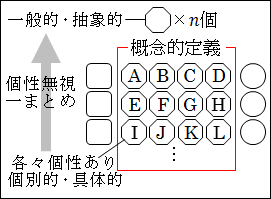
例えば、1人1人のヒトは個別的で具体的な太郎、次郎、花子、菊子、…と決して全く同じヒトではありません。
しかし、「ヒト」という概念的定義の下に、私達はn人の「ヒト」として理解することができます。
そして、このとき、1人1人のヒトはその個性を失い、n人の「ヒト」という抽象的な概念の集合になります。
図26.4.大量のデータの個性消失と数値化 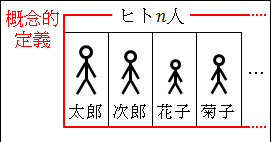
具体的な観察時に注目する要素
そして、概念的定義の下に集められた事例の集合を実際に具体的に観察するときに注目するのは、その概念的定義を具体化した操作的定義です。
操作的定義を変数と捉えて、その具体的な内容を変数値として扱います。
図25.7.変数と変数値 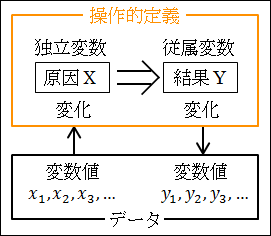
ヒトの例に則して、「性別による身長の違い」、つまり「男性の方が女性よりも身長が高い傾向がある」といった概念的定義を調べたいとします。
このとき、操作的定義として「性別」と「身長」を調べればいいことになります。
そして、「性別」が独立変数であり、「身長」が従属変数となります。
図26.4.大量のデータの個性消失と数値化 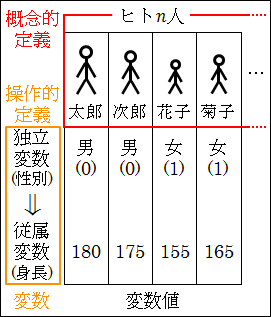
「性別」の変数値は、「男」と「女」になります。
一般家庭で何の準備もなしに使うことのできる統計ソフトとしては、ほとんどのパソコンに入っている EXCEL 等がありますが、これを使うとき、「男」を「0」、と「女」を「1」と置いたりすることが多いです。
このことからも分かる通り、言葉で表されていた概念が数字(数値)として処理されているのが分かります。
「身長」の変数値は、最初から数字(数値)で表されます。
センチメートルを単位として「180」や「155」といったものになります。
こうして、独立変数が「性別」であり、具体的な内容である変数値が「男(0)」か「女(1)」かである。
従属変数が「身長」であり、その具体的な内容である変数値が「180」や「155」などとなる。
変数値を調べる
大量に集めた「ヒト」で、変数に従って変数値を観察します。
独立変数の変化が、従属変数の変化に影響するかを確かめます。
そして、大量の事例を観察した結果として、「男(0)」のときの「身長」の値と「女(1)」のときの「身長」の値を比較していき、「男性の方が女性よりも身長が高い傾向がある」ことを確認できたとします。
これがもし定性的研究であったら、「太郎」と「花子」という個別的で具体的な「ヒト」を観察して記述することになります。
おそらく「太郎」と「花子」の比較などで、一般的で抽象的な「性別による身長の違い」を説明して記述することになるでしょう。
しかも、それは、あくまで個別的で具体的な事例「ヒト」から推論しただけです。それだけでは、一般的で抽象的な「性別による身長の違い」までは証明できていません。
少数ではなく大量の「ヒト」を観察して、一般的な傾向を証明する必要があります。
そもそも「一般」という言葉は、「広く全体的に当てはまること」を意味します。したがって、少数の事例だけでは一般性は証明できず、大量のデータを観察することが必要になります。
そして、大量のデータを観察するには、時間や費用・労力の関係で1つ1つの事例を細かく見て行くことができません。
ですから、一般的で抽象的な大量のデータを数値化(数量化)する必要が生じます。
この数量化された大量のデータを用いて、一般的な理論を証明するのが、定量的に研究することなのです。
まぁ、でも、実際にはデータの収集と処理はこんなに単純なものではなく、因果関係や相関関係を認めるには、結構面倒な作業が必要になります。「年齢」などの変数も制御したり、統計学的な処理が必要だからです。さらに、大量に集めたデータが妥当なのか、その処理は適切なのか、といった問題は常について回ります。そうした技術や知識は、大学で学んでもらうとして、科学的手法の大枠を感じ取ってもらえれば今は十分です。
このように、定量的研究でデータを収集します。
1つ1つの個別的で具体的な事例の個性を無視して、一般的で抽象化した概念に当てはまる事例を大量に集めて数字化・数量化します。
この大量のデータによって、仮説に再現可能性があることを証明します。つまり、同じ条件がそろえば、同じ結果が得られることを確認します。
第三者による追試
そして、再現可能性は、第三者による追試を可能にします。
同じ条件がそろえば、同じ結果が得られるので、概念的定義と操作的定義は何か、データとして何を使ったか、どのようにデータを処理したか等を公表すれば、第三者でも同じように、仮説やモデルを再現して本当にそうなのかを検証して確かめることができます。
第三者が追試を行って、仮説やモデルが本当に正しいかを検証してくれれば、自分がデータを集めて実験したときだけ偶々上手く行ったという確率が低くなります。
逆に、第三者が再現できなければ、仮説やモデルは誤りであったということになります。
▼注を飛ばす
某リケジョは、第三者の追試がまったく上手く行かずに偽造・捏造だということが明るみになった。ただし、彼女自身は、自分の仮説が正しいと主張しており非も認めていないので、偽造・捏造と断罪しても仕方ないのかもしれない。
しかし、仮に意図的・故意的な偽造・捏造ではなかったとしても、論文と同じ過程を踏んで実験しても誰も再現できないのだから、やはり科学的・学問的には話にならない無価値な仮説であったとしか言いようがない。しかも、そうした実験を多くの科学者に行わせたという点で、人材・予算・時間の無駄であったため、やはり有害性は高いと言える。とは言え、科学的方法に基づいて仮説を形成・検証し、第三者が追試するという過程が、嘘を早期に発見し、修正するのに役立つことがよく分かってもらえたかと思う。
▲注に戻る
以上の説明から分かる通り、定量的研究でも、概念的定義と操作的定義を明確にして、それを変数と捉えて、数値化しなければなりません。
ですから、数字や数量を数学的・統計的に分析する前にも、定性的研究による観察対象の分析が必要になります。
つまり、定量的研究は、定性的研究で明らかにされた説明を一般化して実証することを目指していることが分かります。3.数学の重要性
さて、前の章で、変数という考え方を最初に出したときに、数学でよく使われると言いましたが、変数と数学は相性がいいです。
まず、数学では、公理 axiom という最も基本的・基礎的なな仮定である命題をいくつか置きます。この公理のまとまりを公理系 axiomatic system と呼びます。
この公理が推論を行う上で最初の前提となります。
定義から分かる通り、この公理は仮定であり、それ自体は正しいことを証明することはできません。ただ真である、つまり、正しいものとして扱うと決めているだけです。
しかし、正しいと仮定することで矛盾なく様々な証明を行うことができます。したがって、公理は、正しいと仮定すると色々と便利だから、そう仮定していると思ってもらって構いません。
科学の多くの発見は、特に根拠はないが「こう仮定したら色々と矛盾なく説明できるぞ」という発想から始まることも多いです。もちろん、その仮定が突飛であったり、明らかに現実と矛盾することだと問題があり意味のないものになります。しかし、ある仮定を置いて、それを元に考えると、色々な事柄を説明できるとしたら、それは非常に有益です。科学の多くの理論等は、このような発想から組み立てられて、その後にデータ収集や実験で、本当に現実でも同じことが起きているかを証明しています。
このように、数学の公理も、仮定から始まります。とは言っても、公理となった仮定も、元を正せば、何かを観察した結果思いついたりするものであることがほとんどですが。とりあえず、数学の場合は、公理は証明なく正しいものとして扱っています。
そして、公理から正しいと証明された命題を定理と言います。英語では theorem です。
図26.5.公理と定理と実証 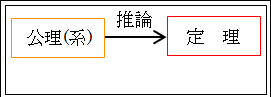
例えば、皆さんが数学で、理解させられた、あるいは、暗記させられた定理に、三平方の定理「直角三角形の斜辺の2乗はその他の辺の2乗の和に等しい」というのがありました。数式で表すならば「c2=a2+b2」と書かれることが多いです。
この三平方の定理は、正しい前提である公理から出発して、正しく推論した結論です。
正しい前提から正しく推論された結論は、正しくなります。ですから、三平方の定理は正しいです。
しかし、これは言ってみれば、論理の世界でゴチャゴチャと考えているだけです。要は、頭の中で考えたこと、といった感じです。
そして、個別的で具体的な直角三角形を考えているというよりも、一般的で抽象的な直角三角形を考えていることになります。
つまり、論理の世界で、一般的で抽象的な事柄を思考していることになります。
図26.5.公理と定理と実証 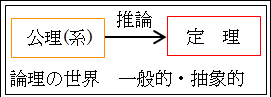
頭だけで考えたことは、往々にして現実と乖離していることが多いです。頭だけで考えていると、美しく理想化されていることが多いですが、複雑な現実をそのまま捉えることは難しく、思いがけない見落としも有り得るので、浮世離れしがちです。ですから、現実に即しているかを確かめる必要があります。
そこで、実際に色々な個別的で具体的な直角三角形の三辺の長さを測ってみます。そうすると、論理的な結論と一致します。
皆さんも、学校や塾で、実際に色々な直角三角形で試させられた経験があるかと思います。
つまり、現実での観察・測定と論理の世界での推論が一致していることが分かります。論理の世界は現実の世界を予測したことになります。
図26.5.公理と定理と実証 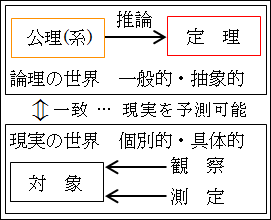
このように、数学は論理的であり、論理の正しさを追求しているが、結果として現実の事象と一致することが分かります。
そのため、数学は科学を研究する上でメチャクチャ強力な武器になります。言い換えるならば、数学は科学の分析の道具になります。こう言うと、数学の専門家は、「いや、数学はそれ自体美しいのだ」とか、「数学が目的そのものだ」と言ってくるかもしれませんが。私も、そうした数学自体に美しさがあるという面は否定するどころが賛成しますが、多くの人にとっては数学は科学の分析の道具だということもまた事実です。
もし対象を数式によって表すことができれば、それは数学の論理的な正しさを利用できることを意味します。これは論理を重んじる科学や学問にとって非常にありがたいことです。
例えば、「距離は、速く移動することを長い時間かけるほど長くなる」と言葉で記述したとします。
これを数式で表すと「距離=速さ×時間」となります。数式で表すと曖昧さが排除できます。
また、数式の変数値を色々と変えることで、どのような結果が得られるかも予測できます。しかも、その予測は、数学によって論理的な正しさの裏付けもされています。
確かに、時速10kmで1時間走ったらどうなるかは、実際に実験を行わなくても、数式を用いれば10kmという結果が予測できます。
このように、数学的に、つまり、変数を数式で表すことで、誰がいつでも何度やっても、同じ変数値を入れれば、同じ結果が得られます。再現可能性があるということになります。
したがって、科学では、曖昧さを排除して一意的にしか解釈できないようにするためにも、言葉で表現し記述されていた現象を数式や論理式で表すことが目指されます。
図26.6.定性と定量―記述と数式 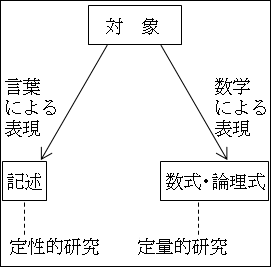
このように、数学が、対象を数値化して分析する研究である定量的研究と非常に相性がいいことが分かります。
特に、これが上手く行っているのが、自然科学である物理学や化学の分野です。この科目では、数式が大量に出てくることからもイメージしやすいかと思います。
しかし、世の中の現象は、数式で表せられることの方が少ないです。4.統計学の活用
そのようなときでも、何とか「数学的な正しさ」を利用できないかと考えて生み出されたのが統計学です。
ですから、統計学は応用数学になります。
図26.6.定性と定量―記述と数式 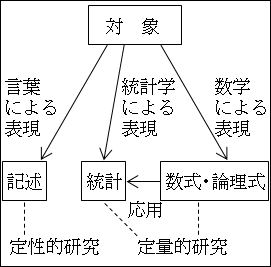
先程の「性別による身長の違い」は、まさに、統計学的手法によって説明されたものです。
このように、統計学は、大量のデータを観察し分析する以外にも、数式で表し難い事柄を数値化・数量化して定量的研究を行うことを可能にしてくれる学問です。
なお、応用数学である統計学は、「数学的な正しさ」を利用するために生み出されたものですが、数学程にはその正しさが保証されていないことに注意してください。
なぜならば、統計の多くは、通常では数式で表現しにくい対象を、数学的に分析するために、数値として「解釈」しているためです。
図26.6.定性と定量―記述と数式 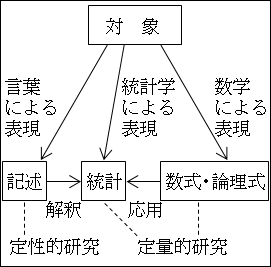
「解釈」とは、矛盾すると思われることを、矛盾なく説明することです( 第21章 論理ピラミッド -現象型の問題-)。
この場合の「解釈」は、数式などのように数値化・数量化で表現することが難しいのに、数値化・数量化して、矛盾なく説明することを意味します。
したがって、統計では、対象を数値化して説明するという「解釈」が妥当なのかといったことが常に問題になります。
また、集めるデータも世の中のすべての場合のデータを集めることも事実上不可能です。
ですから、どうしても世の中すべてのデータの中の一部を調べていることも常に意識しておかないといけません。
集めたデータは全体の中の一部なのだから、その一部が全体を代表していると「解釈」しても問題がないのかも確認しておく必要があります。
なお、いわゆる理系の学問では、数値化の「解釈」に幅が生じることは少ないですが、いわゆる文系の学問では、数値化の「解釈」自体が議論を呼ぶことが多いのは、先に説明した通りです(第25章 科学的方法 4 観察可能な含意と概念的定義と操作的定義)。
このように、応用数学である統計および統計学は、数学ほどには「数学的な正しさ」がないことを肝に銘じておいてください。
統計が使われているから、「数学的な正しさ」があるとは限りません。「解釈」の妥当性について、いつも以上に注意が必要になります。
逆に言えば、統計を使うことで「数学的な正しさ」があるように見せかけることができ、相手を自分にとって都合が良い方向に誘導することもできます。皆さんは大学で統計学を学んでも、悪用して相手を騙したりしないでくださいね。
こうした説明をすれば、理系だろうが文系だろうが、高校での数学の学習が大切なのがよく分かるはずです。数学的な考え方を理解して、自分で操れなければ、数学それ自体だけではなく、科学的な分析自体もできないことを意味しているからです。
でも正直に言えば、現代ではパソコンの統計ソフトを使って、教科書に書かれた数式を組んで、データを入力してしまえば、勝手に計算してくれるので、数学が少々苦手でもある程度は困らずにやり過ごすことができるのも事実です。
ですが、教科書に載っていないことや新しいことを考え出そうとするとき、数学的な知識や素養があまりにも低いと、必ず困ることになるはずです。ですから、数学が入試科目にない私立文系に進むことを考えている生徒も、大学で真面目に勉強する気があるのならば、数学を捨てずにちゃんと勉強してくおいてださい。
4 定性と定量の役割
定性的研究と定量的研究が相互に補い合いながら、学問的・科学的がなされていることが理解できたかと思います。
定性的研究では、仮説やモデルを形成します。
しかし、これは、個別的で具体的な少数の事例を包括的に説明する仮説でしかありません。本当に多くの場合に当てはまる一般的で抽象的な仮説やモデルであるかは分かりません。
そこで、定量的研究で、仮説やモデルが事実と合致しているかを確認し、証明します。
したがって、定量的研究では、数値化・数量化することになります。
しかし、逆に言えば、数値化・数量化できない対象は、定量的研究になじまないことになります。
定量的研究では、大量のデータを数値化して、変数値を変えて、その結果として変数がどうなるのかを観察しました。
図26.7.仮説検証と変数 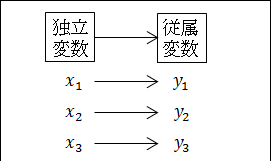
ここで、もしデータを数値化できなければ、変数値を変えることができません。
変数値が変えられないと、変数が変わることもありません。
変数が変わらないということは、原因である独立変数が変わらないのだから、結果である従属変数も変わることはありません。
したがって、変数値が1つの場合のみしか観察できないことになります。つまり、変数値が異なる場合どうなるのかは観察できません。
図26.7.仮説検証と変数 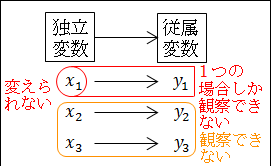
つまり、本当に原因である独立変数が変われば、結果である従属変数が変わることが観察できないので、仮説やモデルの検証ができないことになります。
図26.7.仮説検証と変数 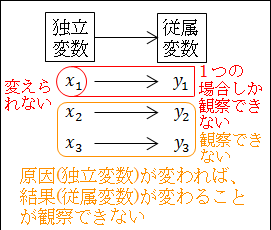
さらに、条件をそろえることができない、つまり、独立変数と従属変数を除くその他の変数を同じにして、独立変数の1つだけ変えることができない場合も同様で、検証ができないことになります。
色々な変数が好き勝手に動くと、独立変数の変数値が変わったために従属変数が変わったのか、その他の変数が変わったから従属変数が変わったのかが判断ができません。
図26.7.仮説検証と変数 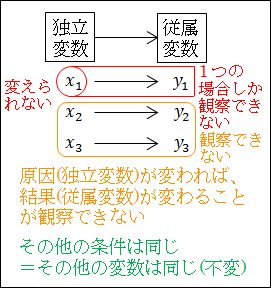
観察対象がこのように適切に数値化・数量化できない場合は、検証が難しい、あるいは検証ができないことが多くなります。
例えば、思想や歴史といった人文科学の学問にこの傾向が強いです。
思想や歴史的な事象において、1つだけ条件(変数)を変えて、結果がどのように変化するかは検証することができないことは、誰にでも容易に想像がつきます。ある特定の人物が一人だけいる場合といない場合に分けて、誰が歴史を検証できるでしょうか。または、歴史的に決定的と思われる行為があった場合と無かった場合に分けて、その他すべての条件を同じにして再現できる人はこの世にいません。1.ミュンヘンの教訓の仮説形成―定性的
もう少し具体的な例で考えましょう。今回は、ミュンヘンの教訓という事例で考えてみます。
ミュンヘンの教訓 the Lesoon of Munich とは、軍事力を背景とした瀬戸際政策を行う国家に対して妥協してはならない、という歴史的教訓です。
これは、国際政治、外交における方針として、戦争を回避するためにも、かなり強く信じられている教訓です。
まずは、このミュンヘンの教訓が導かれる背景を見てみましょう。
第二次世界大戦が起きる前に、ヒトラーはドイツ(独)の総統として、軍拡と領土拡張を試みていました。
イギリス(英)やフランス(仏)は、第一次世界大戦の悲惨さから、戦争だけは起こすまいと考えて、ドイツの拡張主義に対して宥和的でした。つまり、英仏は、ドイツの要求に対して寛大に受け入れる政策をとっていました。
特に、当時の覇権国家であるイギリスの対独姿勢は、戦争回避のためにかなりの宥和的でした。
具体的には、次のような流れがあります。
1935年に、英独海軍協定を締結して、イギリスはドイツの軍拡を認めました。
1936年に、ドイツが非武装地帯であったラインラントに進駐すると、結果としてイギリスはそれを認めました。
1938年3月に、ドイツがオーストリアを併合しても、ドイツもオーストリアも同じドイツ民族だからと考えて、これを認めました。
そして、1938年9月には、今のチェコにあるズデーテン地方の併合を要求しました。ヒトラーから見れば、ズデーテン地方にもドイツ人が多く居住していたため、オーストリア併合と同じ様に民族自決の論理でした。
さすがに、イギリスとフランスは、一体いつまでドイツは拡張しようとしているのか不安になりました。
そこで、英仏独伊の4カ国の首脳が、ミュンヘンに集まって会談をしました。これがミュンヘン会談です。
その会談では、ヒトラーはズデーテン地方の併合を最後に領土の拡大要求をしないと約束しました。
イギリスとしては、ズデーテン併合を認めるか認めないかの2つの選択肢がありました。
そして、イギリス首相のネヴィル・チェンバレンは、ズデーテン併合を認めました。
ドイツの要求を却下したら、チェンバレン首相は、第一次世界大戦のような戦争になるかもしれないと考えたからです。
このとき、ズデーテン地方の併合を認めたかわりに、ドイツの領土拡張は終わり戦争も起きずに万々歳と、多くの人が思いました。
実際、ミュンヘン会談の後にイギリスに帰国したチェンバレン首相は、平和を持って帰ったと大衆に歓迎されました。
このとき、チェンバレン首相の宥和政策を徹底的に批判したのが、チャーチルです。後の第二次世界大戦を戦った首相です。ただし、第二次世界大戦前には、チェンバレン首相を叩くチャーチルは少数派であり、逆に皆から叩かれていましたが。叩かれていましたが、チャーチルが正しかったことは直に明らかになります。
ヒトラーは、1939年3月にチェコスロバキアを解体して、ドイツの支配下に置きました。英仏はこれに懸念を表明するも、軍事行動を起こしませんでした。宥和政策の継続です。
さらに、ヒトラーは、1939年9月1日に、ポーランドに侵攻しました。ここに来て、英仏はようやく軍事行動を起こし、ドイツに対して宣戦布告しました。この後の第二次世界大戦の悲惨な結果は、皆さんが知っての通りです。
結局、現在考えられているのは、1938年段階でのドイツの再軍備は未だ十分ではなく、このときに、英仏が強気に出てヒトラーの要求を却下しておけばよかったということです。
ヒトラーからすれば、この段階で戦争の準備ができていないので、戦争に打って出ることは難しかったはずです。仮に戦争になっても、あの段階では、未だ英仏の軍事力の方が強く、第二次世界大戦ほど長期化せず、被害も小さく済んでいたと考えることができます。
また、英仏の度重なる宥和政策が、ヒトラーに対して誤ったメッセージを送ってしまったとも考えられています。つまり、ヒトラーに、英仏は戦争を回避したいあまり、本格的に介入して来る確率は低い、あるいは、その可能性はないと思わせてしまったということです。横からの口出しくらいなら無視もできるので、他国への領土侵略に対する足かせが非常に弱くなります。もし口を出すだけで軍事介入して来ないと判断されたら、戦争準備ができてしまえば、英仏が準備する前に、さっさと既成事実を作り上げてしまおうと考えるのも納得が行きます。
そして、このことから、ミュンヘンの教訓として、軍事力を背景とした瀬戸際政策を行う国家に対して妥協してはならないということが導かれています。2.ミュンヘンの教訓の仮説検証―定量的
このミュンヘンの教訓は、第二次政界大戦後の冷戦でもアメリカの外交戦略の内の柱の1つとなりました。
確かに、このミュンヘンの教訓が導かれた経緯と内容を知ると、かなり説得的に思えます。
しかし、本当にミュンヘンの教訓が言うように、瀬戸際政策を行う国家に対して妥協しなかったら、第二次世界大戦は起きなかったのかは分かりません。
歴史は1回限りの出来事です。ミュンヘン会談で、チェンバレン英首相がドイツの要求を却下した場合を実際に試して観察することができません。タイムマシンで過去に戻って、チェンバレン首相を説得して、譲歩すればドイツの拡大を止められずに大戦争になることを教えることはできませんから。
そして、個別的で具体的なこの歴史的出来事を、数値化・数量化して一般化・抽象化されたモデルで考えることも難しいです。この仮説検証の難しさを実際に見てみます。
とりあえず、定量的研究をするにあたって、「宥和政策を取れば、戦争を回避できず」、「強硬政策を取れば、戦争は回避できるか、戦争になっても被害を抑えられる」かを調べたいわけです。
そうすると、原因たる独立変数は、「どの政策を取るか」となります。
具体的な変数値は、「宥和政策」を取るか、「強硬政策」を取るか、のいずれかになります。
この独立変数の変化に応じて、結果である従属変数がどのように変化するかを観察する必要があります。したがって、結果たる従属変数は「戦争と被害の状況」となります。
具体的な変数値は、「戦争勃発」か「戦争回避・被害減少」か、といったところになります。
もう少し具体的に言うと、「宥和政策」を選択すると「戦争勃発で被害が大きい」と予測されます。
「強硬政策」を選択すると、「戦争回避あるいは被害を小さく抑えられる」ことが予測されます。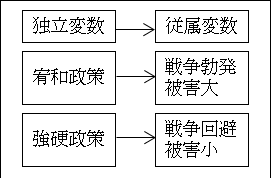
そして、それ以外の変数は変わってはいけないので、固定しないといけません。しかし、瀬戸際外交を取る相手国の軍事力の大きさや、国際環境、同盟の有無、経済力、こうした条件(変数)は固定できるとも思えません。しかも、こうした軍事力・国際環境・同盟・経済力といった条件は、無視できないのは、ちょっと考えただけで分かります。これらが、結果たる従属変数に影響を与えないとは考え難いからです。
ですから、妥協案として、相手国の軍事力・国際環境・同盟・経済力などが類似した事例を集めて観察することにします。
これを踏まえた上で、何とかモデルを形成するとしたら、瀬戸際政策を取る相手国が覇権を狙えるような大国であることがまず必要です。
そして、その大国が、覇権を狙って強硬策を取ることも必要です。
さらに、ヒトラーと似た状況を考えるなら独裁体制であることも必要かもしれません。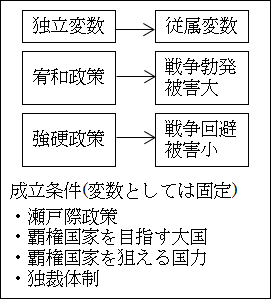
こうした条件をそろえた上で、原因である独立変数の変数値として、「宥和政策」をとるか、「強硬政策」をとるかで、結果である従属変数が「戦争勃発」か「戦争回避」のどちらになるかを確かめないといけません。
それでは、仮説が正しいか検証をするのですが、実験ができないため、せめて歴史を振り返って、類似した事例を集めることにします。
では、このような事例は一体いくつあるでしょうか。
第二次世界大戦後も戦争や紛争は数多くありましたが、こうした条件が揃った事例があるかと言われれば、微妙なところです。とりあえず、見てみましょう。
まず、独立変数が「強硬政策」の場合に、従属変数がどうなったかを観察します。
第二次世界大戦後、朝鮮戦争が起きました。
第二次世界大戦後に朝鮮は、ソ連の支配下にある北朝鮮こと朝鮮民主主義人民共和国と、アメリカの支配下にある南朝鮮こと大韓民国に分断されていました。そこで、北朝鮮が韓国に侵攻して戦争が始まりました。
ミュンヘンの教訓の下でアメリカ大統領トルーマンは参戦することをためらいませんでした。参戦したと言っても、形式的には国連軍です。でも、実質的にアメリカ軍が中心であり、そこに戦場である韓国軍が加わっており、日本が後方支援をしていました。
ソ連は武器支援などを積極的にしましたが、正式に軍を動かすことなく、直接は戦っていません。その代り、北朝鮮側には、中国共産党が義勇兵という形で、戦力を大量投入しました。
戦争の結果、アメリカの被害は甚大でした。しかし、ソ連との直接交戦は避けられました。もし米ソで直接戦っていたら、被害は更に拡大していかもしれませんが、それは今となっては分からないことです。
さて、この結果は、ミュンヘンの教訓通り、強硬政策をとることで、最悪の事態は回避できたと考えていいのでしょうか。
その他にも、キューバ危機があります。ソ連が、アメリカの裏庭であるカリブ海のキューバに核ミサイル基地を設置したことに、アメリカが激怒しました。
アメリカ大統領ケネディは、戦争も辞さない覚悟を示しつつも、ソ連がミサイル基地の撤去を行う余地を残しておきました。見事に最悪の事態の戦争は回避できました。しかし、一歩間違えると核戦争に発展する危険もありました。
こうして朝鮮戦争やキューバ危機を通じて、ミュンヘンの教訓が正しかったのか微妙な事例もありますが、ミュンヘンの教訓が正しいと言えそうな事例も見つかります。
では、逆に、独立変数が宥和政策の場合、従属変数はどうなるでしょうか。
これは、第二次世界大戦後、さらに事例が少ないです。
冷戦中はアメリカがミュンヘンの教訓の下に、瀬戸際外交を許さないことが多かったのですが、ソ連が崩壊して冷戦が終わってからは、アメリカの覇権が決定的になりました。ですから、アメリカの覇権に挑戦できるような国家はありませんでした。
これでは、ミュンヘンの教訓の仮説を検証することが十分にはできていないことが分かります。つまり、正しいとも間違っているとも断定できないことになります。
でも、独立変数が強硬政策のときは、最悪の事態を回避できたと考えてもよい事例が見つかっているので、正しい確率がそこそこありそうだとも考えられます。それでも、物理法則ほどの確信を持っては、断定できません。確かに、数量化できず再現不可能な事例は、仮説検証が難しいのが分かります。
それでも21世紀になると、ロシアがソ連の時代程ではないにしろ、再び力をつけて来ました。中国も世界第2位の経済大国になり同時に軍拡も進めています。そして、アメリカはアフガンやイラクでの戦争で疲弊してきています。つまり、再度ミュンヘンの教訓を検証することができる状況がそろってきています。
そして、オバマ大統領は、強硬政策ではなく宥和政策をとっています。
アメリカの国力が低下している中で争うことは避けたいこと、平和を守りたい思いなどがあります。
こうしたオバマ大統領の姿勢を見て、中露は積極的に膨張策に出ています。
特に中国の覇権主義は年々強くなっています。日本の近海の東シナ海での活動が活発化しています。さらに、南シナ海はアメリカの影響力が比較的弱いことから、中国が積極的に進出して、ヴェトナムやフィリピンとの衝突が起きています。
▼注を飛ばす
2014年、2015年には、ロシアがクリミア半島を占領しようが、アメリカは経済制裁を科す程度だ。今もウクライナを巡って対立は続いている。中国は南シナ海への進出、東シナ海への進出を試みているが、アメリカは口先で少し言う程度で、本気度があるように見えない。中露の膨張は止まる様子がなさそうに見える。ここで、中露両国が力を蓄えていけば、周辺諸国との緊張はますます増すだろう。
また、中東のISIL(Islamic State in Iraq and the Levant イラク・レバントのイスラム国)の問題も泥沼化しており、ここが新たな火種になって何か起きることはないか不安要素になっている。アメリカがシリアのアサド政権が化学兵器を使用した時に、強硬姿勢を取らなかったのが間違いであったという批判をする者もいる。
▲注に戻る
もちろん、これはアメリカ側について、現在の国際秩序から大きな利益を得ている日本の視点から見た見方でもあります。
中露から見れば、アメリカが主導する国際秩序は面白くないので、壊せるのなら壊してしまいたいと考えるのも当然と言えば当然です。
このように現在、ミュンヘンの教訓を検証するためには良い状況ができていると考えられます。
このまま宥和政策を続けたとしても、中露の拡張・膨張主義が止まれば、ミュンヘンの教訓は誤りであったことが分かります。ミュンヘンの教訓が正しいなら、宥和政策を取れば、戦争は不可避的なはずだからです。
オバマ大統領には、ミュンヘンの教訓という仮説を検証するためにも頑張ってもらいたいですね。宥和政策で中露が拡張主義を止めるのかどうか見ものです。
なお、忘れてはいけないのが、宥和政策による「平和」の意味です。
宥和政策を続けていれば戦争が起きず、平和に見えます。これはヒトラーが領土要求をしても認めている段階では、イギリスは戦争を回避できていたことかからも分かります。
ですから、中露が要求したことを丸呑みしていけば、戦争は起きません。領土をよこせと言われれば、「分かりました」と差し上げればいいだけです。でも、それで「平和」が保たれたと言っても、欺瞞もいいところです。大国の思惑に犠牲にされた周辺諸国は堪ったもんじゃありません。
さらに、もしミュンヘンの教訓が正しかった場合、つまり、瀬戸際外交を続ける国家に対して、宥和政策をとると拡張主義が止まらないとしたら、なおさら周辺諸国は堪ったもんではありません。宥和政策が続く限り、周辺諸国は常に大国の必要以上の圧迫と脅威にさらされるからです。
さらにさらに、もしかしたら、既に宥和政策をしていたために、間に合わない状況になってしまっているかもしれません。
ヒトラーが戦争準備をして総力戦体制を作り上げたために、イギリスが軍事介入したときには、もう甚大な被害を出さざるを得ない状況になったように、現在もそうなってしまうかもしれません。
なお、国連に過度に期待を持っている人がいるので、もう一つ付け加えると、この場合、国連は常任理事国の中露が拒否権を持っているので、まず機能しないかと思います。
さて、このように、数値化・数量化できない対象は、定量的研究になじまないことが分かりました。
原因である独立変数以外すべて同じように再現することができない観察対象は、数値化・数量化できない対象であり、検証が難しい、あるいは、検証ができません。
再現できないのなら、大量に似た事例を集めてみてはどうだろうかと考えます。しかし、似た事例を大量に集めることも難しいです。
しかも、数少ない似た事例を見ても、本当に原因である独立変数以外がすべて同じと見なしても問題ないくらいのかが不明な場合が多いです。独立変数以外の他の変数が、結果である従属変数とは無関係にあるのかの判断が難しいからです。
以上、定量的研究に馴染まないものは検証が難しいことからは、定性的研究の弱点を明確に浮かび上がらせます。
定性的研究のみで終わる研究は、定量的研究と異なり、検証ができないか、検証が難しいことを覚えておいてください。
したがって、定性的研究における内容の正しさを判断するとき、データである史料や文章などが本当に存在しているのか、そのデータは正しいのか、そこから導かれる解釈や推論は論理的なのか、といったことが中心になります。
仮説やモデルが事実と合致しているのかどうかは、実験などによって検証して証明できていません。
仮説は仮説のままと言うことです。
ですから、定性的研究による因果関係などは、大量のデータを統計的手法で分析する定量的研究によって明らかにされる因果関係などとは、質が異なることに注意しておいてください。
ただし、このことは、定性的研究が定量的研究に劣っていることを意味しません。
研究対象の性質上仕方ないことなのです。分からない物は分からない。しかし、放置しておく訳にもいかない。だから、合理的な説明を試みている。こういった具合です。
定量的研究をすれば分かるのではなく、定量的研究にできないだけなのです。ですから、定性的研究だろうが定量的研究だろうが、どちらでも分からないことには変わりはありません。
5 まとめ
以上で、科学的方法による研究を、観察対象のどこに注目して、どのように表現するかで研究の種類が大きく2つに分けられることを学びました。定性的研究と定量的研究の2つです。両者は相互に補い合いながら、学問的・科学的な研究は進んで行きます。
定性的研究とは、対象の性質に注目して分析する研究です。研究内容は、言葉で表現して記述することになります。対象の包括的な説明を目指します。
最も抽象的な概念的定義と、それを構成する本質的な要素や性質として具体化した操作的定義を言葉で丁寧に表現します。
複雑な対象がどういったものなのか理解可能な形に推論できます。これが、記述的推論でした。
図26.1.定性的研究と記述 画像クリックで拡大 
なお、記述的推論では、操作的定義に沿って、質的データを集めて分析するとになります。
この質データは様々です。インタビューやアンケート調査といった聴き取り調査。歴史的史料や議事録等の文章。物質や現象の観察結果や発掘された遺跡などです。どれも個別の具体的な物事です。
図26.2.概念的・操作的定義・データと論理構造 
対象の大枠や本質が理解ができたら、因果関係の有無を考えます。この因果関係についての推論を因果的推論と言いました。
定性的研究の特徴として、一度の研究において、観察の対象となる数は少なくなる傾向があることです。
個別的で具体的な物事を丁寧に観察して、対象の本質とは一体何なのか、何故そうなっているのか、といったことを分析するため、人的資源的にも時間的にも大量のデータを調べることが難しくなるからです。
そのため、定性的研究は、事例研究や少数事例の比較研究といったものになります。
| 定性的研究 | |
| 着眼点 | 対象の性質 |
| 表現法 | 記述 言葉による説明 |
| データ | 質的データ |
| インタビュー アンケート調査 観察結果 文章 歴史的史料 遺跡 | |
| 目的 | 対象の包括的説明 仮説・モデルの形成 |
| 方法 | 概念的・操作的定義の抽出 記述的推論 因果的推論 |
| 研究例 | 事例研究 少数事例の比較研究 |
| 欠点 | 仮説検証(再現可能性の確認)が困難 |
こうして仮説やモデルが形成されます。しかし、定性的研究では、個別的で具体的な事例を観察して抽象化したものであり、仮説形成段階でしかありません。仮説が正しいかどうかを確かめるためには、仮説検証をする必要がありました。
そこで、仮説検証に役立つのが定量的研究です。
定量的研究とは、対象を数字や数量として分析する研究です。研究内容は、数字や数式で表すことになります。仮説やモデルが常に成立すると証明することを目指します。
定量的研究で扱われるデータは、量的データと呼ばれます。数字や統計などが、これにあたります。対象1つ1つの個別の内容よりも、全体を数字に落とし込んで処理することが重要になります。
集められる大量のデータの1つ1つは、個別的で具体的な要素は無視されます。それぞれの事例は個性を失って、一般的で抽象的な概念的定義が規定する本質や特徴を持つものとして数字に置き換えられます。
つまり、対象を数値化・数量化します。
図26.3.大量のデータの収集

そして、概念的定義の下に集められた事例の集合を実際に具体的に観察するときに注目するのは、その概念的定義を具体化した操作的定義です。
操作的定義を変数と捉えて、その具体的な内容を変数値として扱います。
図25.7.変数と変数値

大量に集められた個別的で具体的な量的データは変数値となります。
このデータである変数値が具体的に変化すると、変数である操作的定義がどのように変化するのかを観察します。
これで、仮説やモデルから予言された結果が得られれば、仮説やモデルが現実と合致しており正しいことが確認できます。
こうして定量的に観察された対象は、数式で表されるなど数学的に表されると、言葉で書く場合の曖昧さを排除でき、因果関係がより明確になります。
数式などで表すことが難しい対象でも、応用数学である統計学を用いると、対象を数値化・数量化として「解釈」して、数学的な表現に近い形で表現することができました。
図26.6.定性と定量―記述と数式

こうして仮説やモデルが検証できれば、個別的で具体的な説明は、一般的で抽象的な説明として認められるようになります。
そして、これは部分的な説明から法則的で一般的な説明である理論に発展していくことに繋がっていきます。
| 定量的研究 | |
| 着眼点 | 数値や数量 |
| 表現法 | 数学・統計 数式・論理式による説明 |
| データ | 量的データ |
| 実験 大量の観察結果 統計資料 | |
| 目的 | 対象の因果関係の証明 仮説・モデルの検証 |
| 方法 | 大量のデータの分析 変数と変数値を用いた分析 再現可能性の確認 |
| 研究例 | 理論研究 多数事例の比較研究 |
| 欠点 | 数値化・数量化できない対象は分析不可 |
以上が、定性的研究と定量的研究の概観でした。両者は対立するものではなく、相互に補い合う関係で、役割分担があるだけです。
定性的研究は、仮説やモデルを形成する際に主に用いられます。定量的研究は、定性的研究で形成された仮説やモデルが正しいかを検証するのに役立ちました。
また、一般的で抽象的な仮説やモデルが持つ、何時でも何処でも誰がやっても、同じ条件をそろえれば同じ結果が得られるという再現可能性は、定量的研究によって確認することになります。
定性的研究が少数事例の個別的で具体的な研究に対して、定量的研究は大量の事例を研究することになるからです。
これは逆から見れば、数値化・数量化が難しい研究、再現可能性がない研究は、定量的研究になじみません。
そもそも仮説検証において、条件をそろえて、変数を上手く操作して観察するには、実験をしたり、大量の事例を集める必要があります。
図26.7.仮説検証と変数

しかし、こうした実験や大量の事例の観察が難しい場合は、実際に事実と合致しているかは不明のままです。
定量的研究ができないので、定性的研究の段階に止まり、仮説は仮説のままになります。そのため、定性的研究は論理的な正しさのみが拠り所となります。
以上、学問と科学の方法について学んできました。
前の章では、科学的方法の大枠を学び、どのような手順で研究が進むのかについて学びました。
この章では、その科学的方法の手順において、対象をどのように分析するのかについて学びました。
| 定性的研究 | 定量的研究 | |
| 着眼点 | 対象の性質 | 数値や数量 |
| 表現法 | 記述 言葉による説明 | 数学・統計 数式・論理式による説明 |
| データ | 質的データ | 量的データ |
| インタビュー アンケート調査 観察結果 文章 歴史的史料 遺跡 | 実験 大量の観察結果 統計資料 | |
| 目的 | 対象の包括的説明 仮説・モデルの形成 | 対象の因果関係の証明 仮説・モデルの検証 |
| 方法 | データから概念的・操作的定義の抽出 記述的推論 因果的推論 | 大量のデータの分析 変数と変数値を用いた分析 再現可能性の確認 |
| 研究例 | 事例研究 少数事例の比較研究 | 理論研究 多数事例の比較研究 |
| 欠点 | 仮説検証(再現可能性の確認)が困難 | 数値化・数量化できない対象は分析不可 |
次からは、今まで「証明できた」とか「科学的に正しい」とか言ってきましたが、その「正しさ」といったものが、どういう意味なのかについて考えて行くことにします。
前頁:第25章 科学的方法
ページトップへ:第26章 定性的研究と定量的研究
次頁:第27章 実証主義と反証主義