前頁 |▼| 次頁
第2章 推論方法の基礎
論理的な主張には、結論に加えて、それと関連性のある根拠が必要でした。これを支えるものが、正しい知識に基づくことと正しく推論することでした。そこで、正しく推論するために気を付ける点を色々と確認していきます。
| 目次 |
| 1 命題と前提と結論 2 肯定と否定 3 全称と特称 4 ド・モルガンの法則 連言と選言 5 条件法 6 まとめ テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 命題と前提と結論
推論の基礎について、最も有名で分かりやすい三段論法と絡めながら学びましょう。この三段論法を中心に、正しい推論の条件等を分析していきます。
それでは(2.1)を見てください。
| (2.1)次の推論は正しいか。 <大前提> 魚は泳ぐ <小前提> マグロは魚だ [結論] よって、マグロは泳ぐ |
大前提は論証の出発点としての一番大きい前提です。小前提は結論を導く上で必要な前提です。論理的主張で言えば、前提は根拠にあたるものです。
そして、大前提の方が小前提に比べて、一般的で抽象性が高いです。
「マグロ」は「魚」の中の1つの種類です。大前提は、魚類の1つである「マグロ」に絞っておらず、「魚」全体について述べています。魚類の1つである「マグロ」について述べている小前提よりも、一般性が高いことが確認できます。
ここで、大前提・小前提・結論はそれぞれ内容があり、意味を持っています。これらは命題と呼ばれています。
論理学の約束事では、命題は真・偽の判断を行えるものでなければなりません。真とは命題の内容が正しいことを意味しており、偽とは命題の内容が正しくないことを意味しています。
論理学では真・偽判定が行えるものが命題ですから、疑問形や命令形は基本的に命題とはなりません。
例えば、「これはペンですか」という疑問形のものを考えてみてください。その質問に対しては、ペンか否かは答えられます。
しかし、「これがペンである」ならば真、「これがペンではない」のであれば偽ということではありません。これは質問に答えているだけで、命題自体の真・偽判定になっていません。
「これはペンです」という肯定形ならば、実際にペンなのか否かで真・偽判定ができます。でも、「これはペンですか」という疑問形では、命題自体が正しいかどうかは判断しようがありません。
したがって、疑問形は命題にはなりません。
また、「ペンをとって」という命令形の場合はどうでしょうか。「ペンをとってあげる」ならば真、「ペンをとってあげない」のならば偽というわけではありません。疑問形の場合と同じで、命令形では、命題自体の真・偽の判定ができません。
したがって、命令形も命題になりません。
ちなみに、たとえ肯定形だとしても、単なる感想等も命題たりえません。
「私はペンが欲しい」といった場合、欲しければ真、欲しくなければ偽と判断できるわけではありません。「マグロは泳ぐ」と違って、人の気持ち自体は、正しいか間違っているかは判断しようがありません。
実際にペンを買ったら真、買わなかったら偽となるわけでもありません。買えなくても「ペンが欲しい」という意志を本当に持っているかもしれません。
したがって、意志や感想といったものも命題にはなりません。
このように、論理学では、推論の正しさと、その結果によって命題の真・偽判定ができるものですから、疑問形・命令形・意志等の主観に関わる外から正しいかどうか分からないモノは扱わないことになります。
しかし、日常的な場面で論理的思考を扱う場合には、それではやや狭すぎます。実際、複数の前提や条件から、「~をすべきだ」といった提言等はよくなされます。
そこで、日常的な意味で論理的思考という場合、命令形や疑問形も、意志等の主観も命題として扱うことにします。
そのときの注意点として、できるだけ真・偽の判定がしやすいように表現することです。
疑問形なら「これはペンですかと言った」、命令形なら「ペンをとってと言った」、意志なら「私はペンが欲しいという意志を持っている」といった形に読み換えて、できるだけ外から見て判断しやすいようにしておくことが重要になります。
主観的過ぎる表現では、周囲の人は何も判断できません。
根拠のない結論だけの主張では最初から同じ意見の人しか納得できなかったように、主観的過ぎる表現は、それと同じことを思っている人にしか通じません。
論理的に物事を考えるとき、それを表現するときは、できるだけ外見から判断できる、客観的に、表現するようにしましょう。
2 肯定と否定
三段論法を使用するための条件をより深く分析するために、前提や結論の各命題をより緻密に分析していきます。
| (2.1)次の推論は正しいか。 <大前提> 魚は泳ぐ <小前提> マグロは魚だ [結論] よって、マグロは泳ぐ |
(2.1)の命題の述語に注目してみます。
どの命題も肯定形で表されています。「魚は泳ぐ」「マグロは魚だ」「マグロは泳ぐ」すべて肯定形となっています。
もちろん文には「~である」といった肯定形もあれば、「~ではない」といった否定形もあります。否定形を記号で表すならば¬となります。
なお、論理学で否定というとき純粋な意味での否定になります。これは日常の否定と比べると分かりやすいです。
日常で「好きではない」というと、純粋に「好き」を否定しているのではなく、「嫌い」まで含んだ意味合いを持つことが多くあります。「嫌い」と直接言うと角が立つので、やんわりとさせるため「好きじゃない」と言ってみたりすることがあります。
かと思うと、「好きではない」が、「普通」の意味でも使われたりもします。「好きでも嫌いでもない」といったどっちでもない特別な感情は無い、といった意味合いです。
日本語はなんて曖昧て難しいんだと思った人は心配いりません。英語でも「嫌い」と言うとき、hate や dislike のような嫌いな気持ちを全面に出したくないので、I don't like it といった具合にぼかすことが多いです。日本語だけではないので、安心できますね。
このように、日常で用いられる「~ではない」といった否定は、多様な意味があり、純粋に否定することもあれば、その逆の意味を表したりもします。会話の流れ、文脈なしに判断することは中々難しいものです。
これに対して、論理学の否定は純粋な意味での否定のみを表します。
「好きではない」といったとき、「普通だ」や「嫌いだ」という意味合いは一切含まないことになります。
この「好き」という感情のみを純粋に否定していることをもう少し詳しく見てみます。
好き嫌いに関する感情で、「好き」「普通」「嫌い」といった幅があるとします。

「好きではない」と言ったとき、「好き」が否定されて、「普通」と「嫌い」が残ることになります。
図2.1.否定

このように、論理学では、「好きではない」と言ったとき、「好き」か「好きではない」かの二者択一になります。「好き」ということが否定されるだけで、「普通」なのか「嫌い」なのかは分かりません。
また、どこかから好きで、どこから好きではないのかも不明ですが、「好き」か「好きではない」かでバッサリと切ります。
これが論理学の否定の意味です。純粋に否定しているだけで、それ以上は何も語っていないことに注意してください。
日常では、誤解が生じないようにするために、「普通」の場合はそのまま「普通だ」と言ったり「好きでもないし嫌いでもない」と言うべきかもしれません。ある程度ハッキリ言っておくべき時とそうではない時があるり、臨機応変に対応するしかないです。
しかし、論理的思考では、最初の取り掛かりとして、ザックリと「否定」を論理学的な意味合いで使うことを基本とします。
もちろん文脈等で適切に判断する必要がありますが、慣れない内は割り切って考えるとよいでしょう。
なお、「好き」といった段階性のあるコトの否定ではない場合、対義語で言い換えてもよいことがあります。
例えば、生物学上の性別を考えているとき、「男」を否定すると「男ではない」となりますが、これは「女」を意味しています。
生物学上と初めに言ったのは、社会学上で考えれば、LGBT等といった分類ができるからです。この場合では、「男ではない」が「女」であることを意味するとは限らなくなってしまいます。
そして、否定で重要なのは、二重否定です。「~ではない」といった否定語を2回重ねて使うと肯定になります。
「好きではないではない」は「好きだ」ということになります。論理的思考では、二重否定は肯定形として捉えて単純化します。
確かに日常での二重否定の使われ方と異なることがよくあります。
例えば、友人と昼食を何にするか考えていて、
「ラーメンはどう?」と訪ねると、
友人が「なくはないかなぁ」と答える。
このような場合の「なくはないかなぁ」とは、「ありだ」という積極的な賛成ではなく、まぁ反対する程でもないとかそういった消極的な意味合いのことがあります。
それでも、論理的思考では、二重否定は肯定形として処理してしまいます。複雑なことを単純化して、考えやすくしたいからです。
もちろん、慣れてくれば二重否定に含まれる微妙なニュアンスを汲み取って考えるようにすればいいです。あくまで最初の段階では肯定形に単純化して考えるとよいということです。
3 全称と特称
もう一度(2.1)に戻って意味をよく考えてみます。
| (2.1)次の推論は正しいか。 <大前提> 魚は泳ぐ <小前提> マグロは魚だ [結論] よって、マグロは泳ぐ |
主語の「魚」も「マグロ」も、文として表に現れていませんが、「すべての」「魚」や「マグロ」について表していることに気付きます。
このように「すべての~」という場合を全称(ぜんしょう)と言います。記号で表すと∀で表されます。ちなみに、ローマ字のAが逆さまになっているので、英語では turned Aと読みます。
「すべての魚」「すべてのマグロ」といった形になります。
なお、「すべての~」は「任意の~」とも表されたりします。
「任意」とは、意に任せるですから、一般には、当人の思うがままに、自由に、といった意味です。自由に選べるということだから、何を選んでもよいということになる。何でも選べるということは、全部から選択できるということになる。よって、「すべての~」と同義になります。
「任意の魚」と言った場合は、「魚」を自由に選べるわけですから、どの「魚」についても選べることになり、「すべての魚」と同じ意味になります。
これは図で表すとこのようになります。
図2.2.全称と特称
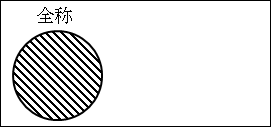
円が「魚」全体を表しており、斜線が「すべての魚」が何を指しているかを表しています。
つまり、円と斜線がピッタリ重なっているので、「すべての魚」と言うと、「魚」という概念全体を表しているのが視覚的に分かります。
これに対して、「すべて」ではない場合、つまり、1以上の一部について述べたいときは、「ある~」と表して特称(とくしょう)と言います。記号で表すと∃ となります。英語ではEが反転しているので、turned Eと読みます。
「ある魚」「あるマグロ」といった形になります。「ある魚」と言ったときには、少なくとも1匹以上の「魚」について述べていることになります。
特称記号は存在記号とも呼ばれることがあります。
「ある魚は美味しい」というとき、「美味しい魚が存在する」ということを表しているからです。「魚」全体の中で、「美味しい魚」とそうでない「美味しくない魚」に分けます。すると「美味しい魚」は「魚」全体の中の一部を表していることになります。
これは特称と同じことを表していることになります。
これは図で表すとこのようになります。
図2.2.全称と特称
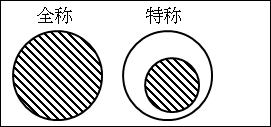
円が「魚」全体を表しており、斜線が「ある魚」が何を指しているかを表しています。
つまり、円全体に対して斜線が一部のみ重なっているので、「ある魚」と言うと、「魚」という概念全体の中の一部の「魚」を表しているのが視覚的に分かります。
全称と特称の関係で注意が必要なのは、「~ではない」が組み合わさったときです。
(2.2)を見てください。
| (2.2)次の命題を否定せよ [結論] すべての人間は道徳的である |
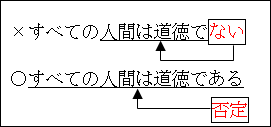
これを否定したとき、「すべての人間は道徳的でない」ではありません。これでは、「道徳的な人間は存在しない」と解釈されてしまいます。
否定の言葉である「ない」が「人間は道徳的である」にしかかかっておらず、「すべて」が否定されていないことになり、正しくありません。
ちゃんと「すべての人間は道徳的である」全体を否定しないといけません。
そして、「すべての人間は道徳的である」を否定すると、「『すべての人間は道徳的である』ということはない」になります。
| (2.2)次の命題を否定せよ [結論] すべての人間は道徳的である 「すべての人間は道徳的である」ということはない |
図で表すと、このようになります。
図2.3.全称の否定
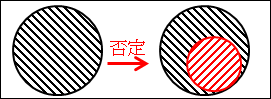
黒の斜線部分が、「すべての人間は道徳的である」です。「人間」の中で、「道徳的である人」が表されています。
赤の斜線部分が、「否定」されている箇所です。「人間」の中で、「道徳的ではない人」が表されています。
これって要するにどういうことなのでしょうか。
「すべての人間は道徳的である」は、100人の人間がいれば100人とも道徳的な人であることです。
「『すべての人間は道徳的である』ということはない」とは、100人の人間がいれば、100人皆が道徳的であるのではなく、中には道徳的でない人もいるということになります。
これは部分否定と考えられます。
そして、一見すると「すべての~」と全称表現ではあるが、内容的には特称になっていることに気付きます。
これは図を見ても明らかです。黒の斜線部分が全体だと考えると、赤の斜線部分が全体の一部になっており、特称の図と同じになっています。
100人中100人皆が道徳的であるということはなく、道徳的でない人も一部に存在することを表しているからです。
「道徳的でない人間が存在している」ことを意味しているということです。
| (2.2)次の命題を否定せよ [結論] すべての人間は道徳的である すべての人間は道徳的であるということはない =道徳的でない人間がいる |
「道徳的でない人間がいる」とは、「ある人間は道徳的ではない」ということと同義です。
| (2.2)次の命題を否定せよ [結論] すべての人間は道徳的である すべての人間は道徳的であるということはない =道徳的でない人間がいる =ある人間は道徳的ではない |
ということは、全称表現「すべての~」を否定すると、特称表現「ある~」となることが分かります。
「『すべてのSはPである』ということはない」は「あるSはPではない」ということです。
もし「すべての人間は道徳的でない」とすると、100人中100人皆が道徳的ではなくなってしまい、道徳的である人間が0になってしまいます。
これは全てを否定しているので、全部否定ですね。
そもそも論理学的には否定というのは、純粋にそのものを否定するだけで、それ以上を意味することはありませんでした。
したがって、「すべての人間は道徳的である」を否定とは、100人中100人が道徳的であることを否定するものです。何人が道徳的なのかは分かりませんが、100人中99人が道徳的でも、100人中1人が道徳的でもいいのです。ともかく、100人中100人皆が道徳的であることを否定しているだけです。
しかし、「すべての人間は道徳的でない」とすると、道徳的である人がまったく存在しないことを意味するので、100人中0人が道徳的であることになります。
これでは「すべての人間は道徳的である」の否定とは意味が違ってしまいます。
なお、全称表現「すべての~」を否定すると、特称表現「ある~」となることの逆のパターン、つまり、特称表現「ある~」を否定すると、全称表現「すべての~」になることも知っておいてください。
| (2.3)次の命題を否定せよ [結論] ある人間は道徳的である |
単純に否定すると、「『ある人間は道徳的である』ということはない』となります。
| (2.3)次の命題を否定せよ [結論] ある人間は道徳的である 「ある人間は道徳的である」ということはない |
「ある人間は道徳的である」は、100人の人間がいれば何人かは道徳的な人が存在していることです。
「ある人間は道徳的であるということはない」とは、100人の人間がいれば何人かは道徳的であることを否定しています。何人かは分かりませんが、道徳的である人がいることを否定しているのです。
これは全部否定と考えられます。
図で表すと、このようになります。
図2.4.特称の否定
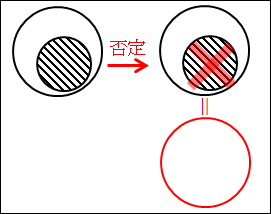
黒の斜線部分が、「ある人間は道徳的である」です。「人間」の中で、「道徳的である人」が表されています。
そして、「ある~」という特称を「否定」しているので、黒の斜線部分が消えることになります。
つまり、黒の斜線部分が表していた「道徳的である人」がまったくいなくなることになります。
よって、赤の円は、「道徳的である人が一人もいない」ことを表すと同時に、「人間」全体で「道徳的ではない人」のみが存在することを表していることになります。
したがって、一見すると「ある~」と特称表現ではあるが、内容的には全称になっていることに気付きます。
100人の中で何人かは道徳的であることはないのだから、道徳的な人なんていないことを意味しています。「道徳的である人間が存在していない」ことを意味しているということです。
| (2.3)次の命題を否定せよ [結論] ある人間は道徳的である 「ある人間は道徳的である」ということはない =道徳的である人間はいない |
「道徳的である人間が存在していない」とは、「すべての人間は道徳的ではない」ということと同義です。
| (2.3)次の命題を否定せよ [結論] ある人間は道徳的である ある人間は道徳的であるということはない =道徳的である人間はいない =すべての人間は道徳的ではない |
このように、特称表現「ある~」を否定すると、全称表現「すべての~」となることが分かります。
「『あるSはPである』ということはない」は「すべてのSはPではない」ということです。
まとめると、全称と特称の関係は、全称を否定すると特称に、特称を否定すると全称になることが分かりました。
| (2.4)全称と特称の関係 すべての ← 否定 → ある 全称の否定 「すべてのSはPである」ということははない || あるSはPではない 特称の否定 「あるSはPである」ということはない || すべてのSはPではない |
このように、
全称、つまり「すべての」ことについて述べているのか、
特称、つまり「ある」一部について述べているのかは、
論理的思考で重要になるので、常に意識しておかなければなりません。
本当は記号を用いる方がスッキリとするのですが、この講義では数学や論理学を勉強しているわけではないことに加えて、あまり多くの記号を使用すると拒絶反応を示す人が少なからずいるので、∀、∃、¬の記号は使いません。
4 ド・モルガンの法則 連言と選言
三段論法について大体理解できたところで、より複雑なことを考えられるように、新しい概念を導入します。
より複雑に考えるとは、命題をより複雑なものにするという意味でもあります。
今まで見てきた命題は「魚は泳ぐ」といったように、1つの文、つまり単文で表されていました。
そこで複雑に考えるとは、1つの命題を2つの文、つまり複文にしたり、1つの文でも概念が3つ以上現れる等のように複文に書き直せるような形を考えます。
たとえば、「太郎も花子も足が速い」という文は、「太郎は足が速い」と「花子は足が速い」という2文を1文にまとめたものと分析できます。
また、「タケヤは太っているが、足が速い」というのは1つの文ですが、2つの文「タケヤは太っている」と「タケヤは足が速い」を接続詞「が」を使って1文にしていると分析できます。
このように、1つの命題の内容をより複雑にする方法について説明していきます。1.連言
まず(2.5)を見てください。
| (2.5)次の命題を2つの命題に分けよ。 [命題] 太郎も花子も足が速い |
(2.5)では、「太郎も花子も足が速い」とは、主語が2人あるので、述語を補足してやると、「太郎は足が速く、花子も足が速い」ということが分かります。
| (2.5)次の命題を2つの命題に分けよ。 [命題] 太郎も花子も足が速い 太郎は足が速く、花子も足が速い |
さらに「かつ」という単語を用いて表します。「かつ」は論理学では連言と呼ばれます。英語ではandです。
「A かつ B」と言えば、「A」と「B」が対等に並立していることになります。
| (2.5)次の命題を2つの命題に分けよ。 [命題] 太郎も花子も足が速い 太郎は足が速く、花子も足が速い 太郎は足が速く、かつ、花子も足が速い |
すでに分かる通り、「太郎は足が速い」ことと「花子は足が速い」ことの2文があることが明白になっています。この2文が、最初の1つの命題を2つに分けたものとなります。
| (2.5)次の命題を2つの命題に分けよ。 [命題] 太郎も花子も足が速い <命題> 太郎は足が速い <命題> 花子は足が速い 太郎は足が速く、花子も足が速い 太郎は足が速く、かつ、花子も足が速い |
このように、2つの命題を1つにまとめるとき、連言である「かつ」を用いて考えると、命題の構造が見えやすくなります。
視覚的に捉えるなら、このようになります。
図2.5.連言
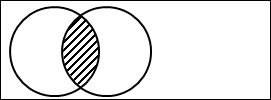
2つの円は「太郎は足が速い」と「花子は足が速い」です。
斜線で塗られている2つの円の重なっている部分が、連言「かつ」で結ばれた部分を表しています。つまり、斜線部分が、「太郎は足が速く、かつ、花子も足が速い」を表しています。
ただし、日常的な表現を論理学の「かつ」を用いて分析する場合には注意点があります。
論理学の分野で「かつ」を用いると、時間の前後関係を無視することになります。
具体例として(2.6)を見てみましょう。
| (2.6)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> 太郎は車を止めた <命題> 太郎は居眠りをした |
(2.6)の2つの命題「太郎は車を止めた」と「太郎は居眠りをした」を「かつ」で繋げると「太郎は車を止めて、かつ、太郎は居眠りをした」となります。
| (2.6)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> 太郎は車を止めた <命題> 太郎は居眠りをした [命題] 太郎は車を止めて、かつ、太郎は居眠りをした |
これを日常的な表現に直すと、「太郎は車を止めて、居眠りをした」や「太郎は車を止め、そして居眠りをした」となります。
| (2.6)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> 太郎は車を止めた <命題> 太郎は居眠りをした [命題] 太郎は車を止めて、かつ、太郎は居眠りをした 太郎は車を止めて、居眠りをした |
ここで、2つの命題の順序を逆にして「かつ」を繋いでみるとどうなるでしょうか。
「太郎は居眠りをした」「かつ」「太郎は車を止めた」となるわけです。
| (2.6)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> 太郎は車を止めた <命題> 太郎は居眠りをした [命題] 太郎は車を止めて、かつ、太郎は居眠りをした 太郎は車を止めて、居眠りをした 太郎は居眠りをして、かつ、太郎は車を止めた |
これでは「太郎は居眠りをして、車を止めた」となり、太郎が居眠り運転していることになります。
| (2.6)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> 太郎は車を止めた <命題> 太郎は居眠りをした [命題] 太郎は車を止めて、かつ、太郎は居眠りをした。 太郎は車を止めて、居眠りをした × 太郎は居眠りをして、かつ、太郎は車を止めた 太郎は居眠りをして、車を止めた |
このように論理学の「かつ」は時間的前後関係を無視しているので、日常的な意味での論理的思考を行う際は、時間的前後関係を意識した表現にしておかなければなりません。
また、「かつ」は、時間的前後関係と因果関係だけでなく、もう1つ気を付けておくべきことがあります。それは逆接の意味も含んでいることがあるということです。
日常の表現に直すなら「しかし」や「が」といったものです。
| (2.7)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> タケヤは太っている <命題> タケヤは足が速い |
(2.7)の2つの命題「タケヤは太っている」と「タケヤは足が速い」を「かつ」で繋げると「タケヤは太っていて、かつ、タケヤは足が速い」となります。
| (2.7)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> タケヤは太っている <命題> タケヤは足が速い [命題] タケヤは太っている、かつ、タケヤは足が速い |
これを日常的な表現に直すと、「タケヤは太っているが、足が速い」や「タケヤは太っているけど、足が速い」、「タケヤは太っている。しかし、足が速い」となります。
| (2.7)次の2つの命題を、「かつ」を用いて1つの命題にまとめよ。 <命題> タケヤは太っている <命題> タケヤは足が速い [命題] タケヤは太っている、かつ、タケヤは足が速い タケヤは太っているが、足が速い |
「タケヤは太っている、かつ、タケヤは足が速い」を「タケヤは太っていて、足が速い」とすると、日常的な感覚からいくと少し変に感じます。
この理由は接続詞「て」によるものです。
「太っている」ことと「足が速い」ことは多くの人の感覚では両立し難いものだと思われているのにも係らず、「太っている」ことが「足が速い」ことの原因であったり条件であったりすることを示す順接の言葉「て」で繋げていることによります。
このように論理学の連言「かつ」は、日常の感覚では両立し難いものも結びつけることができますが、その際には逆接の表現「しかし」「けど」「が」等で表してやる必要があります。
これを逆手にとれば、逆接で結ばれた2つの命題は、一般的に両立し難いが両立していることを示してることが分かります。
一般的にというのが話を広げ過ぎている場合もあるので、少なくとも、話し手は2つの命題が両立し難いと考えていると判断する根拠になることが多いです。
また、逆接の場合は、後に置かれる命題の方が、主張の力点がある場合が多いこともよく知られています。
(2.7)の場合なら「タケヤは足が速い」ことの方が話し手の言いたいことであるとも考えられます。たとえば、野球で、タケヤが内野ゴロを打ってゲッツーをとられた場合に、タケヤのことを知らない観客がデブ等といった野次を飛ばしたときに、「タケヤは太っているが、足が速い」と擁護してやる。このとき、「太っている」ことを認めつつも、見かけに反して「足は速い」ことを主張しているのです。さらに、そのことはタケヤが足が遅いせいでゲッツーをとられたのではなく、足が速い遅いにかかわらずゲッツーをとれる内野ゴロを打たせた投手側を褒めるべきだ等といった主張を続けていくことができます。
いつもいつも必ずしも逆接の後の命題が主張の力点になるとは限りませんが、そうなることが多いことを覚えておくといいでしょう。
このように論理学の連言「かつ」を用いることで、1つの命題の内容を複雑にできることが分かりました。
そして、日常的な意味での論理的思考を行う際は、「かつ」によって結ばれる2つの命題の関係によっては、順接であったり逆接であったり、時間的前後関係を考えなければならないことも確認しました。
2.選言
次に選言「または」を見ていきます。選言が「または」という言葉で表されることから、「AかBかどちらか」といった意味であることは察しが着くかと思います。
(2.8)を見てください。
| (2..8.1)次の2つの命題を、「または」を用いて1つの命題にまとめよ。 <命題> 太郎は風邪を引いている <命題> 花子は風邪を引いている |
これは「太郎は風邪を引いている、または、花子は風邪を引いている」となります。
| (2.8)次の2つの命題を、「または」を用いて1つの命題にまとめよ。 <命題> 太郎は風邪を引いている <命題> 花子は風邪を引いている [命題] 太郎は風邪を引いている、または、花子は風邪を引いている |
これを日常で使う表現にすると「太郎か花子は風邪を引いている」となります。
| (2.8)次の2つの命題を、「または」を用いて1つの命題にまとめよ。 <命題> 太郎は風邪を引いている <命題> 花子は風邪を引いている [命題] 太郎は風邪を引いている、または、花子は風邪を引いている 太郎か花子は風邪を引いている |
太郎か花子の少なくとも1人のどっちかが風邪を引いていることになります。太郎と花子両方とも風邪を引いていてもいいです。
これを図で表すと次のようになります。
図2.6.選言(包含)
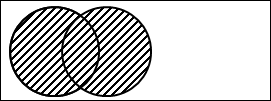
2つの円は、それぞれ「太郎は風邪を引いている」と「花子は風邪を引いている」を表しています。
そして、斜線部分が、選言「または」で結ばれた部分を表しています。
斜線が2つの円全体にまたがっていることから分かる通り、「太郎は風邪を引いている、または、花子は風邪を引いている」とは、2人が風邪を引いているかもしれないし、どちらか1人しか風邪を引いていないかもしれません。いずれにしろ、少なくとも1人は風邪を引いていることが分かります。
このような選言「または」は包含と言います。包含と名称がわざわざ付けられていることから分かる通り、そうではない選言もあることが予測されます。
では、世界史でも習うであろう有名な言葉「コーランか剣か」の場合はどうでしょうか。
(2.9)を見てください。
| (2.9) 剣かコーランか |
「コーラン」を選べばイスラーム教へ改宗することになり、「剣」を選べば戦って死ぬことになる。イスラーム教が拡大した時期に、占領される側がイスラーム教徒の攻撃性を揶揄した言葉です。
| (2.9) 剣かコーランか <命題> 剣を選ぶ <命題> コーランを選ぶ [命題] 剣を選ぶか、または、コーランを選ぶか、どちらか一方のみ選ぶ |
この言葉が表す内容の正しさは置いておくとして、この場合は二者択一でどちらか1つだけを選ぶことになります。両方を選ぶことはありません。
もう1つ例として、ファミレス等でランチセットを注文すると、「ライスまたはパン」が選べることが多いですよね?
この場合、両方頼もうとしたら、どちらかを選ぶように店員から返されるはずです。パンとライス両方選ぶのではなく、どちらか一方のみを選ぶことになります。
このようなどちらか一方のみを選択するような選言「または」は、排他的と言います。包含では両方とも選択できたのに、排他ではどちらか一方のみが選択できます。
これを図で表すと次のようになります。
図2.7.選言(排他)
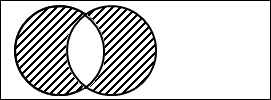
2つの円は、それぞれ「太郎は風邪を引いている」と「花子は風邪を引いている」を表しています。
そして、斜線部分が、選言「または」で結ばれた部分を表しています。
斜線が2つの円全体にまたがっていることから分かる通り、「太郎は風邪を引いている、または、花子は風邪を引いている」とは、2人が風邪を引いているかもしれないし、どちらか1人しか風邪を引いていないかもしれません。いずれにしろ、少なくとも1人は風邪を引いていることが分かります。
このように、「AまたはB」というと、「AとBのどちらか一方のみ」なのか「AとBの少なくとも1つ、したがって、両方であることも可能」なのかを前後関係や文脈から判断しなければなりません。
選言の場合は、少なくとも1つの場合を包含的と呼び、二者択一の場合を排他的と呼ぶことを覚えておいてください。
3.連言と選言の真偽判定
さて、連言「かつ」と選言「または」の意味が分かったところで、命題の真・偽判定の際の注意点について説明します。2つの命題 P と Q を連言で結んだ場合は、「P かつ Q」と表します。
2つの命題 P と Q を選言で結んだ場合は、「P または Q」と表します。
連言にしろ選言にしろ、2つの命題 P と Q それぞれの真・偽の判定が、全体の1つの命題の真・偽判定にどのように関係するかをよく考えてください。
真というのは、正しいことで、事実と合致していることを意味していました。反対に、偽というのは、正しくないことで、事実と合致していないことを意味しました。
2つの円と斜線部分の関係も見ながらいくと分かりやすいです。
さて、P と Q が各々真と偽の2通りずつあるので、全体の1つの命題について 2×2=4 通り考えることになります。
まず連言「かつ」からです。
具体例として(2.5)「太郎は足が速い、かつ、花子も足が速い」を使って考えてみます。P は「太郎は足が速い」で、Q は「花子は足が速い」になります。
「P」が真かつ「Q」が真の場合、「PかつQ」は真となります。
これは2つの命題が正しい場合には、全体の1つの命題も正しいと直感的にも納得できると思いますが、一応詳しく見てみます。
命題「太郎は足が速い」が正しく、命題「花子は足が速い」も正しいことであると言う場合、全体の1つの命題「太郎は足が速い、かつ、花子も足が速い」というのは正しいことが分かります。
「P」が真かつ「Q」が真の場合、「PかつQ」は真となることが確認できました。
「P」が真かつ「Q」が偽の場合、「PかつQ」は偽となります。
これも分かりやすいと思いますが、命題「太郎は足が速い」が正しく、命題「花子は足が速い」は正しくないことであると言う場合、全体の1つの命題「太郎は足が速い、かつ、花子も足が速い」というのは正しくないことが分かります。「太郎は足が速い」と「花子も足が速い」ことは両方とも正しくないと、「太郎も花子も足が速い」とは言えません。
「P」が真かつ「Q」が偽の場合、「PかつQ」は偽となることが確認できました。
「P」が偽かつ「Q」が真の場合、「PかつQ」は偽となります。
これは先程のパターンと逆になっているだけで同じことです。
命題「太郎は足が速い」が正しくなく、命題「花子は足が速い」は正しいことであると言う場合、全体の1つの命題「太郎は足が速い、かつ、花子も足が速い」というのは正しくないことが分かります。「太郎は足が速い」と「花子も足が速い」ことは両方とも正しくないと、「太郎も花子も足が速い」とは言えません。
「P」が偽かつ「Q」が真の場合、「PかつQ」は偽となることが確認できました。
「P」が偽かつ「Q」が偽の場合、「PかつQ」は偽となります。
これも直感的に理解できるかと思います。
命題「太郎は足が速い」が正しくなく、命題「花子は足が速い」は正しくないことであると言う場合、全体の1つの命題「太郎は足が速い、かつ、花子も足が速い」というのは正しくないことが分かります。「太郎は足が速い」と「花子も足が速い」ことどちらとも正しくないのに、「太郎も花子も足が速い」と言うことは明らかに間違っていることが分かります。
「P」が偽かつ「Q」が偽の場合、「PかつQ」は偽となることが確認できました。
こうしてみると、連言「かつ」の場合、全体の1つの命題「PかつQ」が真となるのは、Pが真、Qが真の場合のみ であることが分かります。P か Q かどちらか1つでも偽になると「P かつ Q」は偽になることが分かります。
これは、図2.5.連言 から考えれば、より納得できます。
図2.5.連言

連言が表す斜線部分は、2つの円の重なった部分のみです。「P かつ Q」が真ということは、2つの円が重なっていなる部分ということになります。
それ以外だと偽となります。
例えば、「P が真」で、「Q が偽」のとき、「P かつ Q」を除く「P」の円が斜線部分になります。
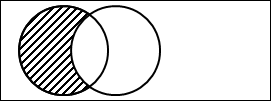
これでは「P かつ Q」ではないので、「P かつ Q」が偽だと一目で分かります。
続いて、選言です。
選言には包含と排他の2種類がありましたが、まず包含的な場合について考えます。
具体例として、(2.8)「太郎は風邪を引いている、または、花子は風邪を引いている」を使います。P は「太郎は風邪を引いている」で、Q は「花子は風邪を引いている」になります。
「P」が真かつ「Q」が真の場合、「PまたはQ」は真となります。
連言の場合と同様に、2つの命題が正しい場合には、全体の1つの命題も正しいと直感的にも納得できると思いますが、一応詳しく見てみます。
命題「太郎は風邪を引いている」が正しく、命題「花子は風邪を引いている」も正しいことであると言う場合、全体の1つの命題「太郎は風邪を引いている、または、花子は風邪を引いている」というのは正しいことが分かります。PかQの少なくとも一方が真ならば、「PかつQ」も真となるので、PとQ両方とも真ならば、当然「PかつQ」は真となります。
「P」が真かつ「Q」が真の場合、「PまたはQ」は真となることが確認できました。
「P」が真かつ「Q」が偽の場合、「PまたはQ」は真となります。
連言の場合と異なり、命題「太郎は風邪を引いている」が正しく、命題「花子は風邪を引いている」は正しくないことであると言う場合には、全体の1つの命題も正しくなります。「太郎か花子は風邪を引いている」という場合、太郎か花子の少なくともどちらか一方でも風邪を引いていれば、全体の1つの命題は正しいことになります。したがって、2つの命題PとQのどちらか一方でも真ならば、もう一方が偽でも全体で真となります。
「P」が真かつ「Q」が偽の場合、「PまたはQ」は真となることが確認できました。
「P」が偽かつ「Q」が真の場合、「PまたはQ」は真となります。
これは先程のパターンのPとQの真偽を入れ換えて、同様に考えればいいです。
命題「太郎は風邪を引いている」が正しくなく、命題「花子は風邪を引いている」は正しいことであると言う場合には、全体の1つの命題も正しくなります。「太郎か花子は風邪を引いている」という場合、太郎か花子の少なくともどちらか一方でも風邪を引いていれば、全体の1つの命題は正しいことになるからでした。したがって、2つの命題PとQのどちらか一方でも真ならば、もう一方が偽でも全体で真となるのも同じです。
「P」が偽かつ「Q」が真の場合、「PまたはQ」は真となることが確認できました。
「P」が偽かつ「Q」が偽の場合、「PまたはQ」は偽となります。
これは直感的に分かりやすいはずです。
命題「太郎は風邪を引いている」が正しくなく、命題「花子は風邪を引いている」も正しくないことであると言う場合には、全体の1つの命題も正しくなくなります。「太郎か花子は風邪を引いている」という場合、太郎か花子の少なくともどちらか一方でも風邪を引いていれば、全体の1つの命題は正しいことになります。しかし、どちらとも正しくないならば太郎も花子もどちらとも風邪を引いていないので、「太郎か花子は風邪を引いている」はどうやっても正しいとは言えないのです。
「P」が偽かつ「Q」が偽の場合、「PまたはQ」は偽となることが確認できました。
連言と異なり選言の場合は、全体の1つの命題「PまたはQ」が偽となるのは、Pが偽、Qが偽の場合のみであることが分かります。PかQかどちらか1つでも真になると「PまたはQ」は真になることが分かります。
これも図で確かめるとより納得いくようになります。
図2.6.選言(包含)

「P または Q」では、2つの円全体に斜線が引かれています。
ですから、「P」か「Q」の少なくとも1つでも真だと、「P または Q」は必ず真となるのは当然と言えます。
そして、「P」と「Q」がどちらとも偽のときは2つの円の外にあることになるので、当然「P または Q」は偽となります。
なお、選言には包含的な場合以外にも、排他的な場合がありました。
「コーランか剣か」や「ライスまたはパン」で見た様な二者択一の意味の「または」の場合には、真・偽の判定が異なってきます。
「P」が真かつ「Q」が真の場合、「PまたはQ」は偽となります。
二者択一なので、両方とも正しいということは有り得ません。ファミレスでは「ライスまたはパン」でライスとパン両方とも選ぶことができないことからも分かります。
「P」が真かつ「Q」が偽の場合、「PまたはQ」は真となります。
「P」が偽かつ「Q」が真の場合、「PまたはQ」は真となります。
二者択一なので、いずれか一方のみを選ぶわけですから、どちらか一方が真で、もう片方は偽であればよいことになります。「ライスまたはパン」でライスを選べばパンが手に入らない、つまり、ライスが真でパンが偽となります。その逆もまた然り。このような場合、「ライスまたはパン」は正しいことが分かります。
「P」が偽かつ「Q」が偽の場合、「PまたはQ」は偽となります。
二者択一でも、どちらとも偽ならば、当然全体で1つの命題も偽となります。
これも図で考えてみましょう。
図2.7.選言(排他)

排他的な選言である「P または Q」では、2つの円から「P かつ Q」の部分を除いて斜線が引かれています。つまり、2つの円全体を表す包含的な選言から、「P かつ Q」を除いたものが、排他的な選言であると言えます。
排他的な選言では「P かつ Q」を含まないので、2つの円が重なり合う部分の「P かつ Q」だと偽になります。
「P または Q」が真であるには、「P」が真のとき「Q」は偽であるか、「P」が偽であるとき「Q」は真であることが必要になるのが分かります。
そして、「P」と「Q」がどちらとも偽のときは2つの円の外にあることになるので、当然「P または Q」は偽となります。
どのような場合に真になり偽となるかをまとめた表を真理値表と言いますが、連言と選言をまとめると表2.1のようになります。
| PまたはQ | |||||
| P | Q | PかつQ | 包含的 | 排他的 | |
| 真 | 真 | 真 | 真 | 偽 | |
| 真 | 偽 | 偽 | 真 | 真 | |
| 偽 | 真 | 偽 | 真 | 真 | |
| 偽 | 偽 | 偽 | 偽 | 偽 | |
この真理値表はことあるごとに使用するので、自分のモノにしておきましょう。
4.ド・モルガンの法則
肯定形の場合を見てきたわけですが、連言と選定に否定が絡むと面白い関係性が見えてきます。(2.10)を見てください。
| (2.10)次の命題はどのような意味か簡単に説明せよ。 [命題] 太郎は足が速い、かつ、花子も足が速い、ということはない |
「太郎は足が速い、かつ、花子も足が速い」を全部否定する、つまり「『太郎は足が速い、かつ、花子も足が速い』ということはない」とした場合、これはどのようなことを意味しているのでしょうか。
記号を使って簡略化して表すと、「『P かつ Q』ではない」となります。
また、日常の表現では、「『太郎も花子も足が速い』ということはない」とも言い換えられます。こうすると少しだけですが、意味が取りやすくなります。
では、「『太郎も花子も足が速い』ということはない」が、どういうことを意味しているのか、改めて考えてみましょう。
考えられる可能性を1つ1つ検討して潰し行けばよいので、場合分けをします。
場合分けは、
「太郎」については「足が速い」か「速くない」かの2通りの場合があり、
「花子」についても「足が速い」か「足が速くない」かの2通りあるので、
それぞれの組み合わせることになり、2×2=4 通りについて検討することになります。
| (i) P かつ Q 太郎は足が速い、かつ、花子も足が速い (ii) P かつ Q ではない 太郎は足が速い、かつ、花子は足が速くはない (iii) P ではない、かつ、Q 太郎は足が速くはない、かつ、花子は足が速い (iv) P ではない、かつ、Q ではない 太郎は足が速くはない、かつ、花子は足が速くはない |
この4通りに場合分けできます。
それぞれの場合が、元の命題「太郎は足が速い、かつ、花子も足が速い、ということはない」つまり「『太郎も花子も足が速い』ということはない」と同じことを言っているかどうかを確認していきます。
(i) P かつ Q の場合から順に考えていきます。
この場合、明らかに「『P かつ Q』ということはない」に反することが分かります。
太郎も花子も両方とも足が速いのに、「『太郎も花子も足が速い』ということはない」と言うと、言われた方は、ん?となります。
(ii) P かつ Q ではない場合はどうでしょうか。
太郎の足が速くても、花子の足が速くなければ、確かに「『太郎も花子も足が速い』ということはない」と言っても差支えはないです。
(iii) P ではない、かつ、Q の場合は、(ii)の P と Q が入れ替わった場合と同じことになります。
花子の足が速くても、太郎の足が速くなければ、「『太郎も花子も足が速い』ということはない」と言っても差支えはないことになります。
(iv) P ではない、かつ、Q ではない場合を最後に見ておきましょう。
太郎も花子も両方とも足が速くはないのですから、「『太郎も花子も足が速い』ということはない」と言ってもいいことが分かります。
以上、(i)~(iv)をまとめると、「『P かつ Q』ではない」は、「P かつ Q」以外の場合を表していることが分かります。当然と言えば当然ですが。
つまり、「P かつ Q ではない」、または「P ではない、かつ、Q」、または「P ではない、かつ、Q ではない」の3つのうちいずれかを表しているということです。
図で表すと、このようになります。
図2.8.連言の否定
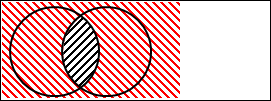
黒の斜線部分が肯定の「P かつ Q」です。
赤の斜線部分が「P かつ Q」を否定したモノです。「P かつ Q」以外のすべてを表していることが分かります。
このことからも、「P かつ Q」を否定すると、「P かつ Q ではない」、または「P ではない、かつ、Q」、または「P ではない、かつ、Q ではない」の3つのうちいずれかを表すことが分かりました。
さらに、「P かつ Q ではない」、または「P ではない、かつ、Q」、または「Pではない、かつ、Q ではない」を分析すると、2つの命題 P と Q のうち、少なくとも1つは否定されていることに気付きます。
少なくとも1つということは、P と Q の両方とも否定されていてもいいわけです。要するに、「P か Q の少なくとも1つは否定される」ということが分かります。
これが何と同じ意味になるか気付いたでしょうか。
少なくとも1つというのは、選言「または」と同じことだということです。
「P または Q」が真とすると、P か Q のうち少なくとも1つは真であることを意味しました。
つまり、「P か Q の少なくとも1つは否定される」は、「P または Q が、否定される」と言い換えることができます。
さらに、「否定される」を P と Q に予め付けておくと「P ではない」と「Q ではない」になるので、「P ではない、または、Q ではない」となります。
このことから、「『P かつ Q』ということはない」とは、「P ではない、または、Q ではない」と同になることが分かりました。
よって、(2.9)は「太郎は足が速くない、または、花子は足が速くはない」ということになります。これが、「『太郎も花子も足が速い』ということはない」の意味です。
まとめると、「PかつQ」全体を否定すると「Pではない、または、Qではない」になるということです。
そして、連言「かつ」を否定すると、選言「または」になることが分かります。
また、この逆、つまり、選言「または」を否定すると、連言「かつ」になることも覚えておいてください。
例えば「『P または Q』ということはない」といった、「PまたはQ」全体を否定すると、「Pではない、かつ、Qではない」となります。
図で表すとこのようになります。
図2.9.選言(包含)の否定
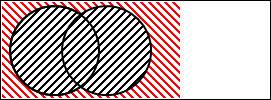
黒の斜線部分が肯定の「P または Q」です。
赤の斜線部分が「P または Q」を否定したモノです。P と Q の2つの円以外のすべてを表していることが分かります。
このことからも、「P または Q」を否定すると、「P ではない、かつ、Q ではない」を表すことが分かりました。
「『太郎か花子は足が速い』ということはない」という場合、「太郎も花子も両方とも足が速くない」ことを意味しています。
「太郎か花子うち少なくとも一人は足が速いということはない」ということなので、「太郎と花子の両方とも足が速い」、「太郎だけ足が速く、花子は足が速くない」、「太郎は足が速くなく、花子だけ足が速い」のいずれの場合も、「『太郎か花子は足が速い』ということはない」の内容に合わないことを確認しておいてください。
ちなみに、選言と言うと、論理学では通常包含的なものを指すことが多いですが、排他的な選言を否定すると、このように図で表されます。
図2.10.選言(排他)の否定
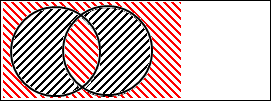
黒の斜線部分が肯定の「P または Q」です。
赤の斜線部分が「P または Q」を否定したモノです。P と Q の2つの円以外か、「P かつ Q」を表していることが分かります。
このことからも、「P または Q」を否定すると、「P ではない、かつ、Q ではない」、または「P かつ Q」を表すことが分かりました。
したがって、連言と選言の関係はまとめると次のように言えます。
つまり、否定されると、連言は選言に、選言は連言になる、ということです。
| 連言「かつ」の否定 ⇒ 選言「または」 選言「または」の否定 ⇒ 連言「かつ」 |
今まで説明して来たこと、連言の命題全体を否定すると否定の選言になり、選言の命題を否定すると否定の連言になるいう法則をド・モルガンの法則と言います。
| ド・モルガンの法則 「P かつ Q」ではない ⇒ Pではない、または、Q ではない 「P または Q」ではない ⇒ P ではない、かつ、Q ではない |
文が複雑になって一読しただけでは分からないときに、ド・モルガンの法則を使用して整理すると、文が何を言っているのか理解しやすくなります。
ちなみに、ド・モルガンとは法則を発案したイギリスの数学者の名前です。
5 条件法
最後に推論方法の基礎的な知識として、条件文についての話です。
1.条件法
条件法とは「PならばQ」といった、2つの命題または概念を「ならば」という語で繋げた文です。
最初に出てくるPが前件、後に出てくるQが後件と呼ばれます。
また、P と Q の関係を見ると、前件Pは後件Qのための条件であり、後件Qは前件Pから導かれる帰結と言えます。
「ならば」を記号で表すと、「⇒」や「→」となりますが、ここでは「⇒」を使うこととします。
条件法「ならば」は、P を仮定して、Q が導ける場合に、「P ならば Q」と結論づけてよい、という約束事です。
これがどういった意味を持つのか見ていきます。論理学での「ならば」も、日常で用いられる「ならば」とは少し違った用いられ方をしています。
2.前件肯定規則
それでは、(2.12)を見てみましょう。
| (2.11)条件法 [命題] 雨が降るならば、試合は中止だ |
(2.12)の命題「雨が降ったならば、試合は中止だ」は、雨が降ると試合が中止になるということを述べています。これ自体は非常に明快です。
前件「雨が降る」が条件と仮定されており、この条件の下に、後件「試合は中止だ」という帰結が導びかれるということです。
つまり、前件「雨が降る」が真であり正しいなら、前件が肯定されることになります。
そすすると必然的に、後件「試合は中止だ」という帰結が導かれることになります。
このような、前件が肯定されるような場合を前件肯定式と呼びます。この前件肯定式は、推論する際に非常に役に立ちます。(2.12)を考えてみてください。
| (2.12)次の2つの前提から得られる結論は何か <前提> 雨が降るならば、試合は中止だ <前提> 雨が降(ってい)る [結論] よって、 |
もちろん答えは「試合は中止だ」です。
前提「雨が降るならば、試合は中止だ」における前件は「雨が降る」で、その前件を肯定する前提「雨が降る/雨が降っている」もあります。
条件法「ならば」が元々前件を仮定して後件を導く機能を持っているので、後件「試合は中止だ」がが導けるわけです。そして、これが結論となります。
| (2.12)次の2つの前提から得られる結論は何か <前提> 雨が降るならば、試合は中止だ <前提> 雨が降(ってい)る [結論] よって、試合は中止だ |
このように、命題「P ならば Q」を前提にして、さらにその前件 P が真であることを前提として、この2つの前提から結論 Q を導くことができます。
そして、これは論理的には常に正しい推論の形式になります。このような条件法の前件を肯定すれば、必ず正しい結論を導ける法則を前件肯定規則と呼びます。
2つのから2つの前提から結論を導いているという点では三段論法です。
公式化するとこのようになります。
| 前件肯定規則 <前提> P ⇒ Q <前提> P である [結論] よって、Q である |
気を付けておかなければならないのは、前件Pが「Pではない」と否定されていた場合には、後件Qが正しいか否かは分からないということです。
例えば、「雨が降るならば、試合は中止だ」で、今「雨が降っていない」とします。
このとき、「試合は中止ではない」と導くことはできません。日常の場面を想定すると、つい「雨が降ってない」ことから「試合は中止ではない」と考えてしまいがちです。
しかし、論理的に考えると、必ずしもそうとは言えないわけです。
「雨が降るならば、試合は中止だ」という命題は、「雨が降る」場合についてのみ言及しているのであり、「雨が降らない」場合については何も言及していません。
「雨が降る」場合に「試合は中止だ」というだけで、「雨が降らない」場合には「試合が中止」なのか「試合は中止ではない」については一切触れていないということです。
ちょっと捻くれた指摘の仕方をすれば、雨が降っていなくても、地震災害等で試合が中止になることだってあるわけです。
確かに、日常において、勝手に「雨が降るならば、試合は中止だ」の裏を読んで「雨が降らないならば、試合は中止ではない」と推測しても、大事にはならない確率は高いです。しかし、学問や原因解明等の論理的思考力が求められる場面では、この論理の飛躍が非常に不味い結果や結論を導くことが多いです。気を付けておいてください。
また、日常の場面でもハッキリ明示しておいた方が良い場合は、「雨が降るならば、試合は中止だ。雨が降らないならば、分からない」や「雨が降るならば、試合は中止だ。雨が降らないならば、試合は中止ではない」としておけばいいでしょう。
その他にも具体例を付け加えるなら、このような論理の厳しさは、法律の条文によく見られます。
条文で、「~等」と完全に条件を限定せずに他にも類似した場合があるよと示したり、「その他~の場合」等といった抽象的な表現にして色々な個別具体的な場合に対応できるようにしています。これは、法律の抜け穴をできるだけ少なくするためにも、ある程度は仕方ないことなんですね。
3.後件否定規則
では、次に(2.13)に移ります。| (2.13)次の2つの前提から得られる結論は何か <前提> 雨が降るならば、試合は中止だ <前提> 試合は中止ではない [結論] よって、 |
答えは「雨は降っていない」です。
前提「雨が降るならば、試合は中止だ」における後件は「試合は中止だ」です。
その後件を否定する前提「試合は中止ではない」があります。
まず、前提「雨が降るならば、試合は中止だ」は、「雨が降る」ことで、必ず「試合が中止」になることを意味しています。
ということは、「雨が降る」場合には、「試合が中止ではない」ことは有り得ないことになります。
よって、後件を否定する前提「試合は中止ではない」ことは、前件の「雨が降る」ことが起きていないコトが分かります。これが結論となります。
| (2.13)次の2つの前提から得られる結論は何か <前提> 雨が降るならば、試合は中止だ <前提> 試合は中止ではない [結論] よって、雨は降っていない |
このように、命題「P ならば Q」と、その後件 Q を偽として、この2つの前提から結論 Pではないを導くことができる法則を後件否定規則と呼びます。
これも2つの前提から結論を導いている点では三段論法です。そして、正しい推論の形式の1つです。
公式化するとこのようになります。
| 後件否定規則 <前提> P ⇒ Q <前提> Q ではない [結論] よって、P ではない |
注意点として、後件Qが「Q」と肯定されていた場合には、前件Pが正しいか否かは分からないということです。
これは前件肯定規則の場合にも前件が否定されている場合と似た話です。
例えば、「雨が降るならば、試合は中止だ」で、今「試合が中止だ」とします。
このとき、「雨が降っている」と導くことはできません。日常では、「試合が中止」であることから「雨が降っている」と考えてしまいがちです。
しかし、論理的には必ずしもそうとは言えないわけです。
「雨が降るならば、試合は中止だ」という命題は、「雨が降る」場合には「試合は中止だ」ということを述べているだけで、その逆の「試合が中止」の場合に「雨が降っている」ことまでは含んでいません。
またしてもちょっと捻くれて言えば、試合が中止になるのは、雨が降っていなくても、地震災害等の場合もあり得るのです。
とは言え、この後件肯定による推論は新しい考えを創り出すときに、非常に有効になります。これは後で6.仮説推論で詳しく説明したいと思います。
しかし、今は論理的に正しい推論の基礎固めなので、後件肯定は推論として正しくないことを肝に銘じておいてください。
条件法の規則を2つ学んだわけですが、前件肯定規則と後件否定規則を混同しないように気を付けておいてください。
前件を肯定したら後件が導け、後件を否定したら前件の否定が導けるこのが正しい推論です。
それ以外の推論は結果として正しい事実を述べていたとしても、推論方法に問題があり、論理的ではないということです。
4 正・逆・裏・対偶
前件肯定規則と後件否定規則のついでに逆・裏・対偶の概念を導入します。
2つの命題 P と Q から構成される命題「P ⇒ Q」を基本の形として考えて、これを「正」とします。
逆とは、P と Q を入れ換えたもので、「Q⇒P」という形です。
裏とは、P と Q を否定したもので、「Pではない⇒Qではない」という形です。
対偶は、逆と裏の両方を併せたもので、「Qではない⇒Pではない」です。
図2.11.正・逆・裏・対偶 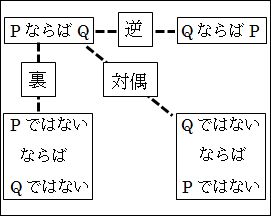
正・逆・裏・対偶の4つは次のような関係があります。
正と対偶の真偽は一致する。
つまり、正が真のとき対偶も真となり、正が偽のとき対偶も偽となる、ということです。
例えば「雨がるならば、試合は中止だ」で考えてみましょう。
対偶は「試合が中止ではないならば、雨は降っていない」となります。正と対偶で同じことを述べているのが分かるでしょうか。
正の命題「雨が降るならば、試合は中止だ」で後件否定規則を用いてみます。
後件の否定は「試合は中止ではない」です。
この2つの前提から、結論「雨は降っていない」が導かれていました。
これは要するに、「試合が中止ではないならば、雨は降っていない」ということです。
したがって、正と対偶の内容は同じことを言っており、真偽が一致することが確認できました。
これに対して、正と逆、正と裏の真偽は必ずしも一致するとは限らない。
つまり、正が真だとしても、その逆は必ずしも真とは限らず、偽になることもある。正が偽だとしても、その逆は必ずしも偽になるとは限らず、真になることもある。
また、正が真だとしても、その裏は必ずしも真とは限らず、偽になることもある。正が偽だとしても、その裏は必ずしも偽になるとは限らず、真になることもある、ということです。
「逆は必ずしも真ならず」とよく言うので、逆は意識されやすいですが、裏も忘れないように注意してください。
逆の例を見てみましょう。
「雨がるならば、試合は中止だ」を正とすると、逆は「試合が中止ならば、雨は降る」です。
これは後件否定規則のところで、犯しやすい過ちとして紹介した後件肯定と同じです。
「試合が中止」だからといって、必ずしも「雨が降る」ことは導きませんでした。「試合が中止」の場合は、雨が降っていなくても、地震災害等の場合がありました。
もっとも明確に真偽が一致しない例を挙げてみます。
「人間ならば哺乳類だ」という命題の逆を考えてください。逆の命題は「哺乳類ならば人間だ」となります。
正の命題「人間ならば哺乳類だ」は事実として問題もなく真とハッキリと言えます。しかし、逆の命題「哺乳類ならば人間だ」では、疑問が生じます。
哺乳類でも犬や猫はどうなのだろうかと。このことから、逆の命題「哺乳類ならば人間だ」は正しくない、つまり偽だと分かります。
このように、明らかに正が真だとしても、その逆は真ではない例があるのが分かります。
以上から、正と逆の真偽は必ずしも一致しないことが分かります。
続いて裏の例を見てみます。
「雨がるならば、試合は中止だ」を正とすると、裏は「雨が降らないならば、試合は中止ではない」です。
これは前件肯定規則のところで、犯しやすい過ちで紹介した前件否定と同じです。
「雨が降らない」からといって、「試合は中止ではない」と必然的に導けるわけではありません。正の命題は「雨が降る」場合についてのみ言及しており、「雨が降らない」場合については何も述べていません。
明らかに真偽が一致しない例を考えてみましょう。
正の命題を「元旦ならば神社にお参りする」とすると、裏の命題は「元旦でないならば、神社にお参りしない」となります。
正の命題「元旦ならば、神社にお参りする」は真であることはすぐに分かります。もし宗教上の理由で否定する人がいれば、ここでは日本人の大多数がするということで真としておいてください。
しかし、裏の命題「元旦ではないならば、神社にお参りしない」はどうでしょうか。
元旦でない日は1年に364日、閏年ならば365日ありますが、神社にお参りすることはないでしょうか。私は高校生の時、毎日のように地元の神社に行っていましたが、これは現代の若者の例外だとしても、観光でもすれば神社を訪れることはあると思います。元旦以外で神社に参拝しないというのは中々正しいとは言えないと思います。よって、裏は偽と言えます。
このように、正と裏の真偽は必ずしも一致しないことも確認できました。
正と対偶のみが真偽が一致し、それ以外の逆と裏は一致するかもしれないし、一致しないかもしれないということは絶対に忘れないでください。
命題の正しさが自明であるが故に、推論方法が正しくないことに気付かず論理を展開することは避けるようにしなければなりません。
なお、正を起点に逆・裏・対偶の関係を見ましたが、起点を移せば、図2.11のように関係を図示できます。
図2.11.正・逆・裏・対偶 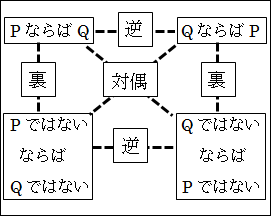
逆の命題を起点に考えれば、正の命題が逆になります。逆の命題の裏は、正の命題の対偶になります。逆の命題の対偶は、正の命題の裏になります。各自で裏から見た場合、対偶から見た場合というのを一度は確認しておいてください。
5 条件法の真偽判定
続いて、命題「P ならば Q」の中身そのものを検討してみましょう。
今までの話では、命題「P ならば Q」が真であるか偽であるかは自明であるかのように進めてきました。
ここで、命題「P ならば Q」を構成している2つの命題、つまり、P と Q のそれぞれの真偽が、命題「P ならば Q」の真偽にどのように関係するかを見ていきます。
P と Q が各々真と偽の2通りずつあるので、全体の1つの命題について 2×2=4 通り考えることになります。
「雨が降るならば、試合は中止だ」を例に考えてみます。前件 P は「雨が降る」で、後件 Q が「試合は中止だ」です。
「P」が真かつ「Q」が真の場合、「PならばQ」は真となります。
これは2つの命題が正しい場合には、全体の1つの命題も正しいと直感的にも納得できると思いますが、一応詳しく見てみます。
命題「雨が降る」が正しく、命題「試合は中止だ」も正しいことであると言う場合、全体の1つの命題「雨が降るならば、試合は中止だ」というのは正しいことが分かります。
「P」が真かつ「Q」が真の場合、「PならばQ」は真となることが確認できました。
「P」が真かつ「Q」が偽の場合、「PならばQ」は偽となります。
これも分かりやすいと思いますが、命題「雨が降る」が正しく、命題「試合は中止だ」は正しくない、という場合です。この場合、全体の1つの命題「雨が降るならば、試合は中止だ」というのは正しくないことが分かります。
この場合、「雨が降っている」にもかかわらず、「試合は中止」になっていないことになります。これでは「雨が降るならば、試合は中止だ」とは言えません。
「P」が真かつ「Q」が偽の場合、「PならばQ」は偽となることが確認できました。
「P」が偽かつ「Q」が真の場合、「PならばQ」は真となります。
これは、先程のパターンと逆になっているのですが、注意が必要です。
命題「雨が降る」が正しくなく、命題「試合は中止だ」は正しい、という場合です。この場合は、全体の1つの命題「雨が降るならば、試合は中止だ」というのは正しくなります。
「雨が降るならば、試合は中止だ」という命題は、「雨が降る」場合についてのみ述べているモノです。したがって、「雨が降る」場合以外に何が起きても、元の命題「雨が降るならば、試合は中止だ」について正しくないとは言いきることができません。
しかし、論理学において、命題とは真・偽を判定できるもの定義しているので、真か偽か決めないといけません。
そこで明確に偽とは判断できないので、「P」が偽かつ「Q」が真の場合、「PならばQ」は真することにしました。
「P」が偽かつ「Q」が偽の場合、「PならばQ」は真となります。
命題「雨が降る」が正しくなく、命題「試合は中止だ」は正しくない、という場合です。この場合、全体の1つの命題「雨が降るならば、試合は中止だ」というのは正しくなります。
これも先程の「P」が偽かつ「Q」が真の場合と同じ理由によります。
論理学でそう定義したからです。
「P」が偽かつ「Q」が偽の場合、「PかつQ」は真となることが確認しました。
条件法「ならば」では、前件Pが真で後件Qが偽の場合のみ「PならばQ」は偽となり、それ以外は真となることが分かりました。
頭がこんがらがって理解できないなら、「雨が降るならば、試合は中止だ」と言う場合に、これが明確に嘘だと言えのは、「雨が降る」にもかかわらず「試合が中止」でない場合のみだと理解しておいてください。
しかしながら、日常の会話で、快晴の下でまさに試合が始まったばかりなのに、「雨が降るならば、試合は中止だ」と言うと、論理的には正しいとしても、頭がおかしい人に思われます。
論理学の世界とは異なる日常では、もう明らかに偽と分かっているコトを前件 P にして「P ならば Q」と発言することは滅多にないので、この違和感に繋がるではないかと思います。
直感的に中々納得行かないかもしれませんが、そういうもんだとして割り切って覚えてください。
真理値表にまとめると表2.2のようになります。
| P | Q | P ⇒ Q | |
| 真 | 真 | 真 | |
| 真 | 偽 | 偽 | |
| 偽 | 真 | 真 | |
| 偽 | 偽 | 真 |
6.条件法と日常での相違点
さて、論理学において「ならば」が、日常での使用方法と趣を異にすることが分かった段階で、もう一つ確認しておかなければならないことがあります。
それは、論理学の「ならば」には因果関係や時間的前後関係を意味として含んでいないことです。これは連言「かつ」もそうだったので少しは理解しやすいかもしれません。
(2.14)を見てください。
| (2.14)次の命題の対偶を書け。 [命題] 勉強しないと、叱られる |
接続詞が「ならば」ではなく「と」ですが、意味的には「P ならば Q」の条件法になっています。「勉強しないならば、しかられる」ということです。
前件「勉強しない」が否定になっているので、これを否定すると二重否定になるので、「勉強する」という肯定になることに注意してください。
とりあえず単純に前件と後件を入れ換えて、それぞれ否定すると「叱られないならば、勉強する」となります。
| (2.14)次の命題の対偶を書け。 [命題] 勉強しないと、叱られる [対偶] 叱られないならば、勉強する |
これでは意味が変わってしまっていることに気が付いたでしょうか。
正の命題では「勉強しない」という事態が最初にあって、その結果として「叱られる」という事態が発生する意味になります。ここには、時間的前後関係が明確にあるわけです。
| (2.14)次の命題の対偶を書け。 [命題] 勉強しないと、叱られる 時間的前後 1 → 2 [対偶] 叱られないならば、勉強する |
しかし、対偶命題「叱られないならば、勉強する」では、「叱られない」という事態が最初にあって、その結果として「勉強する」という事態が発生する意味になります。ここでも、時間的前後関係が明確にあります。
| (2.14)次の命題の対偶を書け。 [命題] 勉強しないと、叱られる 時間的前後 1 → 2 [対偶] 叱られないならば、勉強する 時間的前後 1 → 2 |
正と対偶を比べると、意味合いが変化していることが分かります。
つまり、正の命題では「勉強しない」ことが最初にあり、それが原因となって、「叱られる」という結果を引き起こしています。これに対して、対偶の命題では、「叱られない」ことが最初にあり、それが原因となって、「勉強する」という結果が引き起こされていることになっています。
このように時間的前後関係あるいは因果関係が逆転していることになります。
このようなことが起きる理由に、論理学の「ならば」は、時間的前後関係や因果関係を含んでいないことが挙げられます。
一方で、日常で用いられる「ならば」は、時間的前後関係や因果関係を含んだものであることが多いです。
したがって、対偶命題を考える場合は、文意を保存しながら時間的前後関係や因果関係がおかしくならないように言い換える必要があります。
(2.14)で正の命題の時間的前後関係を保存しながら、対偶命題に書き換えるためには、「勉強する」ことが最初にあり、「叱られない」ことが後に来ることが分かるようにしてやる必要があります。そうすると「叱られていないならば、勉強している」と書き換えることができます。
| (2.14)次の命題の対偶を書け。 [命題] 勉強しないと、叱られる 時間的前後 1 → 2 [対偶] 叱られないならば、勉強する 時間的前後 1 → 2 ↓文意を保存しつつ 日常的表現で言い換える 叱られていないならば、勉強している |
「叱られていないならば、勉強している」が、どういう意味を持っているかよく考えてみてください。
「叱られていない」と言うと、今現在「叱られる」という状態にないことを意味しています。
「勉強している」と言うと、今現在「勉強」している状態を意味します。
そして、「叱られていないならば、勉強している」と言うと、「叱られていない」場合には「勉強している」状態にあるということです。
とすると、「叱られていない」状態を原因として、「勉強している」という結果を導いていないことが分かります。
そして、「叱られていないならば、勉強している」という文からは、「叱られていない」状態の前に「勉強している」状態が先行していることが分かります。
「叱られていない」状態であることは、すでに「勉強している」ことを意味しているということです。
このように、命題を対偶に書き換える際には、時間的前後関係や因果関係等に気を付けて言い換える必要がしばしあります。
6.条件法と日常での相違点
条件法の最後に補足的に、「P ⇒ Q」で大切な考え方に、必要条件と十分条件というモノについて触れておきます。これは高校の数学でも学び、試験でもよく出されるので馴染みが深いと思いますが、敢えて何も知らないという前提で話を進めます。
まず、「P ⇒ Q」が真のとき、
前件P を十分条件、
後件Q を必要条件、
と言います。
なぜこのような名称がついているかと言うと、
PはQであるための十分条件であり、
QはPであるための必要条件である、
と言うからです。
これでは、何が言いたいのかよく分からないと思うので、具体例から考えてみます。
(2.15)を見てください。
| (2.15)十分・必要条件 [命題] マグロならば魚だ |
前件 P は、「マグロ」で、これが十分条件で、
後件 Q は、「魚」で、これが必要条件、
となります。
| (2.15)十分・必要条件 [命題] マグロならば魚だ 前件 ⇒ 後件 十分条件 必要条件 |
「マグロ」は、「魚」であるための十分条件であり、
「魚」は、「マグロ」であるための必要条件である、
ということになります。
「マグロ」と「魚」の関係を考えると、「マグロ」は、「魚」の一部と言えます。
したがって、「マグロ」であれば、自動的に「魚」と言うことができます。
これが、「マグロ」は「魚」であるための十分条件である、ということの意味です。確かに、「マグロ」であることは、「魚」であると言うのに十分な条件と言えます。
「マグロ」から見たら、「魚」という要素は、「マグロ」と言うための十分な条件だと分かりました。
逆に、「魚」から見た「マグロ」はどういったものになるでしょうか。
「魚」であっても、「マグロ」とは自動的には言えません。「魚」には「マグロ」だけでなく、「鮭」や「鯖」も「魚」ですから、「魚」といっても自動的に「マグロ」にはならないわけです。
しかしながら、「魚」というのは、「マグロ」であると言うためには必須の要素となります。
「マグロ」の定義からして、「魚でないマグロ」というのは有り得ません。「マグロ」である限り、「魚」というのは絶対になければならない要素と言えます。
これが、「魚」は「マグロ」であるための必要条件である、ということの意味になります。
したがって、
「前件 P は、十分条件である」という理由は、後件 Q から見れば、前件 P は、後件 Q であると自動的に言える条件だから、
「後件 Q は、必要条件である」という理由は、前件 P から見れば、後件 Q は、前件 P であるために必須の条件だから、
ということが分かります。
この「マグロ」が部分で、「魚」が全体であるという関係は、図で表すと、このようになります。
まず「魚」という集合があります。

この中に「マグロ」という集合があります。
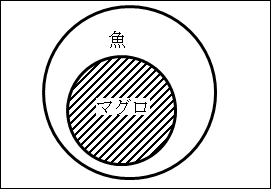
このように、「マグロ」は「魚」の一部ということが分かります。
そして、「マグロ」が十分条件で、「魚」が必要条件であったことから、十分条件と必要条件の関係は、このようになります。
図2.12.十分・必要条件の関係
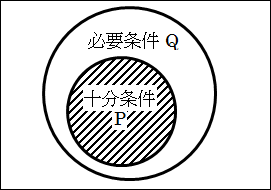
つまり、十分条件 P は、必要条件 Q の部分的なモノだということが分かります。
このことからも、前件 P ならば、自動的に後件 Q と言えますが、後件Q であっても、自動的に前件 P であるとは言えないことが分かります。
十分条件 ⇒ 必要条件 という関係をよく押さえておいてください。
なお、正の逆は必ずしも真ならずでした。
したがって、「マグロならば魚だ」の逆である「魚ならばマグロだ」は、必ずしも真ではないことになります。
実際にも偽であるのは明らかです。「魚」には「鮭」も含まれているので、「魚」といっても自動的に「マグロ」と決まるとは限らないからです。
しかし、「必ずしも真ではない」ということは、もちろん「真である場合もある」わけです。
つまり、
十分条件 ⇒ 必要条件 が真で、
必要条件 ⇒ 十分条件 が真である
という場合もあります。
このように、正と逆のどちらでも真である場合を論理的に同値と言います。いわゆる=で結ぶことができます。
これは、十分条件である P と必要条件である Q が同じだということを意味します。先程の図でいうと、= で結べるということなので、2つの円がピッタリと重なり合うことになります。
論理学では、⇔ という記号を使います。
| 必要十分条件 P ⇔ Q 十分条件 P ⇒ 必要条件 Q が真 必要条件 Q ⇒ 十分条件 P が真 |
(2.16)の命題「x2=1 ⇒ x=±1」を考えて見てください。
「x2=1」とは「x を2回掛けて1 となる」ことを表します。これを満たす数字は、1 と-1 の2つ考えられます。なぜならば、1×1=1、(-1)×(-1)=1、だからです。
| (2.16)必要十分条件の例 x2=1 ⇒ x=±1 真 十分 必要 |
「x2=1」は、「x=±1」であるための十分条件であり、
「x=±1」は、「x2=1」であるための必要条件である、
ということが分かります。
今「十分条件 ⇒ 必要条件」が真であることを確認しました。
では、十分条件と必要条件がひっくり返った場合、つまり、正の逆の場合はどうなるでしょうか。
| (2.16)必要十分条件の例 x2=1 ⇒ x=±1 真 十分 必要 x=±1 ⇒ x2=1 必要 十分 |
「必要条件 ⇒ 十分条件」の真・偽の判断をするということになります。
1×1= 1、(-1)×(-1)=1だから、「x=1」のときも「x=-1」のときも、「x2=1」となります。
つまり、「x=±1 ⇒ x2=1」は真ということが分かります。
| (2.16)必要十分条件の例 x2=1 ⇒ x=±1 真 十分 必要 x=±1 ⇒ x2=1 真 必要 十分 |
つまり、「必要条件 ⇒ 十分条件」が真であることが確認できました。
ということは、「十分条件 ⇒ 必要条件」と「必要条件 ⇒ 十分条件」の両方が真であるということは、「x2=1」と「x=±1」は論理的に同値であることが言えます。
| (2.16)必要十分条件の例 x2=1 ⇒ x=±1 真 十分 必要 x=±1 ⇒ x2=1 真 必要 十分 --------------- x2=1 ⇔ x= ±1 |
数学の方程式を解くときは、この必要十分条件を暗黙の内に用いていることが分かります。
そして、日常の会話でも、このような必要十分条件になっているかを確しかめることで、2つの概念が同じことを意味しているのかどうかは分かります。
逆に言えば、「P は、Q だ」と言う場合でも、「十分条件 P ならば必要条件 Q」は満たしていも、「必要条件 Q ならば十分条件 P」を満たしているとは限らない場合もあります。
例えば、「マグロは魚だ」と言えば、確かに「マグロ=魚」のように考えることもできます。しかし、「魚はマグロだ」と言うと、途端に「ん?」となります。一番美味い魚は何だという話をしているのではない限り、「魚はマグロだ」と言われると、「魚」と言っても「マグロ」以外にも「鮭」等があるから、「魚=マグロ」とするのは、少し変に思えるからです。
このように、同じものという意味で、= で結んで分かりやすく表すことは日常でもよく使われますが、実は、「必要条件 Q ならば十分条件 P」が満たされていないので、論理的に同値ではないことはしばしば見かけます。
こうした何気ない所でも、論理的思考を使って練習して見るのも良いかと思います。
6 まとめ
推論方法の基礎をまとめます。
論理的思考を行うためには、まず命題を具体的に定める必要がありました。つまり、正しいか間違っているかといった真偽の判断が行える言語化された内容とする必要があります。
命題は大きく分けると、肯定文と否定文に分かれていますが、否定の場合は、基本的には裏を読まずに純粋に否定されたモノのみを読み取るのが基本でした。
そして、命題内には全称と特称があります。「すべての~」という意味なのか、「ある~」という意味なのかをしっかりと読み取る必要があります。また、全称を否定すれば特称に、特称を否定すれば全称になりました。
連言「P かつ Q」や選言「P または Q」、条件法「P ならば Q」が使われると、命題が複雑になります。それぞれが何を表しているのかは、図で考えると分かりやすかったです。、また、真理値表で、P と Q が真や偽のとき、連言・選言・条件法の真・偽の判定がどうなるかもしっかりと抑えておく必要がありました。
さて、三段論法の使用条件が分かったところで、三段論法の種類についての話に移ります。
今まで見てきた三段論法は定言三段論法と言います。「SはPである」と断定した物言いになっており、定めて言っていることが分かります。したがって、このような断定調で表された三段論法を定言三段論法と呼びます。
定言三段論法の他にも、選言三段論法と仮言三段論法というのもあります。選言は「Pであるか、またはQである」とどちらかを選ぶような言い方になり、仮言は「PならばQである」という仮に述べるような言い方になります。
そこで、選言三段論法と仮言三段論法の2つをそれぞれ詳しく見ていきます。
前頁:第1章 論理的であるとは
ページトップへ:第2章 推論方法の基礎
次頁:第3章 三段論法