前頁 |▼| 次頁
第3章 三段論法
前提から結論を推論する有名にして典型的な形式、三段論法について学びます。
三段論法とは、2つの前提から結論 を導く推論形式です。英語では sillogism と言います。
大きく別けて、前提の命題が定言・選言・仮言の場合の3つに分類されるので、それぞれの三段論法について見ていきます。
| 目次 |
| 1 定言三段論法 2 選言三段論法 3 仮言三段論法 テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 定言三段論法
(3.1)は(2.1)と同じものですが、章と例文番号を揃えるために(3.1)としただけです。とりあえず、三段論法の中で一番典型的な定言三段論法から学んでいきましょう。
定言三段論法とは、2つの前提から結論を推論する方法ですが、各命題が「~である」等の断定調になっているものです。定めて言うということで仮定や条件といった表現を含んでいません。
| (3.1)次の推論は正しいか。 <大前提> 魚は泳ぐ <小前提> マグロは魚だ [結論] よって、マグロは泳ぐ |
改めて確認からです。
大前提は、論証の出発点としての一番大きい前提です。
小前提は、結論を導く上で必要な前提です。
論理的主張で言えば、前提は根拠にあたるものです。
そして、大前提の方が小前提 に比べて、一般的で抽象性が高いです。
「マグロ」は、「魚」の中の1つの種類です。大前提は、魚類の1つである「マグロ」に絞っておらず、「魚」全体について述べています。
魚類の1つである「マグロ」について述べている小前提よりも、一般性が高いことが確認できます。
図で表すと、大きな円が「魚」で、小さな斜線で塗られた円が「マグロ」ということになります。
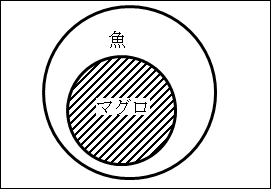
(3.1)では、大前提の命題は「魚は泳ぐ」ですが、これは正しいと言えますので、真と判断できます。
小前提の命題は「マグロは魚だ」ですが、これも正しいと言えますので、真と判断できます。
結論の命題は「マグロは泳ぐ」は、常識的に正しいことなので真と判断できますが、論理的思考の練習として推論から考えてみます。
結論は、2つの正しい前提、つまり、真の大前提と小前提から導かれているので、真と判断できます。正しい前提から正しく推論されたならば、結論も正しくなるからです。
先程の図から考えれば、「魚が泳ぐ」なら、「魚」に含まれる「マグロ」も当然に「泳ぐ」という性質は持っていると推論できるということになります。
さらに詳しく説明すると、
大前提「魚は泳ぐ」は、「魚」の性質について述べています。その性質は「泳ぐ」ことです。
小前提「マグロは魚だ」は、「マグロ」の性質について述べています。その性質は「魚だ」ということです。
そして、結論「マグロは泳ぐ」は、「マグロ」の性質について述べています。その性質は「泳ぐ」ということです。
小前提より「マグロ」の性質は「魚」であり、大前提より「魚」には「泳ぐ」という性質があるため、結論として「魚」である「マグロ」は「泳ぐ」という性質を持つと言えます。
これを整理して、結論「マグロは泳ぐ」
ということになります。
もっと論理関係を分かりやすくするため、記号を使って単純化してみましょう。
そこで、「魚」を「M」と置き、「泳ぐ」を「P」と置くと、
「魚は泳ぐ」は「M - P」と置き換えられます。
さらに「マグロ」を「S」と置くと、
「マグロは魚だ」は「S - M」と置き換えられ、
「マグロは泳ぐ」は「S - P」と置き換えられます。
そうすると、(3.1)はこのように書き換えられます。
| (3.1.1) <大前提> M - P <小前提> S - M [結論] よって、S - P |
大前提と小前提の M で列をそろえてみると、
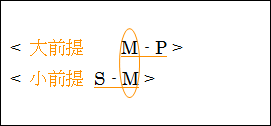
のようになります。
こうしてみると、「S - M - P」となっており、S と P は、M を中心に繋がっていることが分かります。
「S - M -P」の中から、S と P だけを取り出してみると、
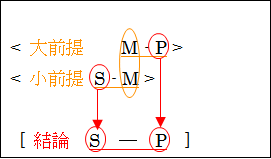
「S - P」となり、結論と同じ構造になります。
つまり、大前提「M - P」と小前提「S - M」によって導かれる結論「S - P」が正しいことが分かります。
なお、日常では前提 の1つを明示せずに発言することが多いです。
例えば「マグロは魚だから泳ぐ」と言った場合、隠れた前提があることに気付けるようにならなければなりません。
「マグロは魚だ(S - M)」を根拠として、結論「マグロは泳ぐ(S - P)」という構造になっており、隠れた前提として「魚は泳ぐ(M - P)」があるわけです。
根拠 「S - M」と結論「S - P」を比べると「M」が欠けており、両者は直接的には繋がりません。それにもかかわらず、正しいものとなっています。
そこで、隠れた前提「M - P」を補うことで、「S - M」と「M - P」から、「S - M - P」という繋がりがあることに気付き、「S - P」が正しいことが分かるのです。
(3.1)では、常識に照らしても簡単に正しいと分かることを例にしているので難しくはないですが、話が込み入って複雑になって来たときや相手の主張の核心をつくときに、隠れた前提を発見することが重要になってきます。
とりあえず、今の話を分かったことをまとめましょう。
三段論法では、
(1)2つの前提命題と結論命題から構成される
大前提と小前提を踏まえて、結論が推論されていました。
(2)どの命題も主語と述語から構成される
大前提、小前提、結論全て主語と述語で表されていました。
(3)3つの概念が現れる
大前提、小前提、結論の中身を見てみると、S、M、Pで構成されてました。
(4)結論命題の主語と述語は、2つの前提に1回ずつ現れる
結論(S - P)に対して、大前提 (M - P)、小前提(S - M)となっていました。
(5)2つの前提命題には共通する概念が必ず1回現れて、結論命題では消える
大前提(M - P)、小前提(S - M)に、共通する概念Mが1回現れており、結論(S - P)では消えていました。
ということが分かりました。
そして、このことを踏まえて、結論(S - P)を推論するために必要な2つの前提の組み合わせは4通りに場合分けできます。
大前提の概念がMとPの2つで主語述語に当てはまるので2通りあり、小前提の概念がSとMの2つで主語述語に当てはまるので2通りあるので、2×2=4だからです。
表3.1定言三段論法の形式
| <前提> M - P P - M M - P P - M <前提> S - M S - M M - S M - S [結論] S - P S - P S - P S - P |
では、(3.2)の場合はどうでしょうか。
| (3.2)次の推論は正しいか。 <大前提> 魚は泳ぐ <小前提> マグロは泳ぐ [結論] よって、マグロは魚だ |
この推論は誤りです。
「魚が泳ぐ」ことと「マグロが泳ぐ」ことから「マグロが魚だ」ということは導けません。確かに、大前提も小前提も真の命題ですし、それから導かれるも結論も真です。
しかし、推論が正しくありません。一見正しく見えても論理的思考ができているとは言えません。
何故でしょうか。
詳しく見ていきましょう。
大前提「魚は泳ぐ」は、「魚」の性質について述べています。その性質は「泳ぐ」ことです。
小前提「マグロは泳ぐ」は、「マグロ」の性質について述べています。その性質は「泳ぐ」ことです。
そして、結論「マグロは魚だ」は、「マグロ」の性質について述べています。その性質は「魚」だということです。
小前提と大前提より「魚」の性質と「マグロ」の性質は「泳ぐ」ことと共通しているのが分かりますが、「魚」と「マグロ」がどのような関係にあるかは何も分かりません。
したがって、肝心の結論「マグロは魚だ」ということを導くことはできません。
これから分かるように、前提に共通項があるからといって、それを単純抜き出して繋いで結論を述べても、正しい推論にならない、ということです。
常に前提 の命題の真偽を確かめた上で、更に推論が正しくできているかを必ず確認しておかなければなりません。
(3.2)は簡単な例なので余り間違うことはありませんが、複雑な論証になったときに、勝手に論理を捻じ曲げないよう気を付けなければなりません。
(3.1)と同じように、(3.2)も記号を使って単純化してみましょう。
「魚」を「P」と置き、「泳ぐ」を「M」と置くと、
「魚は泳ぐ」は「P - M」と置き換えられます。
さらに「マグロ」を「S」と置くと、
「マグロは泳ぐ」は、「S - M」と置き換えられ、
「マグロは魚だ」は、「S - P」と置き換えられます。
| (3.2.1) <大前提> P - M <小前提> S - M [結論] よって、S - P |
(3.2.1)では、大前提「P - M」と小前提「S - M」を「S - M - P」と並べることはできません。
大前提と小前提の述語は、M で共通していますが、主語はそれぞれ P と S となっており、異なっています。
そもそも(3.1.1)では、大前提「M - P」と小前提「S - M」を「S - M - P」と並べることができたのは、大前提の主語と小前提の述語に共通項 M があったからです。
つまり、小前提より「S は M だ」と大前提より「M は P だ」を繋げて読むと、「S は M で、M は P だ」となります。よって、結論「S は P だ」と導ける。このように言うことができました。
しかし、(3.2.1)では、小前提より「S は M だ」と大前提より「P は M だ」を繋げて読むと、「S は M で、P は M だ」となります。よって、結論「S は P だ」と導ける。
このように言えず、「S も P も M だ」くらいしか述べられません。
どうやら三段論法を使用する際には、先に確認した条件の他にも気を付けなければならないコトがあるようです。
三段論法の成立条件には、命題の分析で重要であった全称・特称と肯定形・否定形が大いに関係してきます。
全称と特称で2通り、肯定形と否定形で2通りずつあるので、2×2= 4 通りあります。さらに、先に述べた主語・述語の組み合わせのパターンが4通りあるので、単純計算で44=256通りとなります。
それでは、256通りのパターンを逐一確認して成立条件を探っていきましょう。
というのは冗談で、昔の偉人、古代ギリシアの哲学者アリストテレスが調べてくれていたんですね。256通りの内24種類が三段論法を成り立つことを見つけ出しています。
しかも、4種類といっても、実質的には19種類が三段論法の正しい推論となります。非常にありがたいことです。
それでも19種類すべてのパターンを検討するのは時間がかかるので、ここでは、使用頻度や応用範囲を考えて、4種類のパターンを紹介しておきます。
1.結論が肯定形の場合
まず結論が全称の「すべての~」となり、かつ肯定形の「である」になる。| (3.3.1)結論が全称・肯定形 <大前提> すべてのMはPである <小前提> すべてのSはMである [結論] よって、すべてのSはPである |
次に、結論が特称の「ある~」となり、かつ肯定形の「である」になる。
| (3.3.2)結論が特称・肯定形 <大前提> すべてのMはPである <小前提> あるSはMである [結論] よって、あるSはPである |
(3.3.1)と(3.3.2)の小前提と結論の全称・特称を取り除いてやると、同じ形になります。大前提はそのままです。
| (3.3.3)結論が肯定形 <大前提> すべてのMはPである <小前提> SはMである [結論] よって、SはPである |
これを図解すると、このようになります。
図3.1.結論が肯定形の定言三段論法
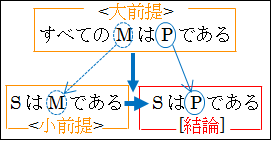
結論が肯定形になる場合は、大前提の主語 M は全称化されており、小前提にも表れて、結論では消えます。そして大前提の述語 P は結論でも述語に残ります。
| (3.3.4)結論が肯定形 <大前提> すべての犬は哺乳類である <小前提> ポチは犬である [結論] よって、ポチは哺乳類である |
(3.3.4)の例のように、自分の中で推論が正しいかどうかを簡単に確認できるものを持っておくとよいでしょう。
2.結論が否定形の場合
続いて、結論が全称の「すべての~」となり、かつ否定形の「でない」になる。| (3.4.1)結論が全称・否定形 <大前提> すべてのPはMでない <小前提> すべてのSはMである [結論]よって、すべてのSはPではない |
最後に、結論が特称の「ある~」となり、かつ否定形の「でない」になる。
| (3.4.2)結論が特称・否定形 <大前提> すべてのPはMでない <小前提> あるSはMである [結論] よって、あるSはPではない |
(3.4.1)と(3.4.2)の小前提と結論の全称・特称を取り除いてやると、同じ形になります。大前提はそのままです。
また、(3.3.3)結論が肯定形の場合と異なり、大前提の主語-述語が「M - P」でなく、「P - M」になっていることに気を付けてください。
| (3.4.3)結論が否定形 <大前提> すべてのPはMではない <小前提> SはMである [結論] よって、SはPではない |
これを図解すると、このようになります。
図3.2.結論が否定形の定言三段論法
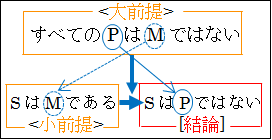
結論が否定形になる場合は、大前提の主語 P は全称化されており、否定の述語 M は小前提にも表れて、結論では消えます。そして、大前提の主語 P は、結論でも述語に残ります。
| (3.4.4)結論が否定形 <大前提> すべての猫は鳥類ではない <小前提> タマは猫である [結論] よって、タマは鳥類ではない |
(3.4.4)の例のように、否定形の場合も自分の中で推論が正しいかどうかを簡単に確認できるものを持っておくとよいでしょう。
残りの15種類も今まで紹介したことを基礎にすれば、簡単に正しい推論であることが分かります。各自で配布資料でよく確認しておいてください。
3.定言三段論法の成立条件
それでは今の議論を踏まえて、(3.5)を考えてみます。| (3.5)次の推論は正しいか。 <大前提> ある学生は勤勉だ <小前提> ある野球部員は学生だ [結論] よって、ある野球部員は勤勉だ |
大前提と小前提の2つ前提が真だとしても、推論が正しくありません。
理由は、大前提と小前提の命題がどちらも特称で「ある~」になっています。
したがって、2つの前提にある共通の概念「学生」があっても、繋げられません。
よって、(3.5)の推論は正しくありません。
一応、推論の形式からの判定だけでなく、意味の面からも詳しく見てみます。
大前提「ある学生は勤勉だ」の意味する所は、学生全体を表しているのではなく、ここでは一人と考えてもいいでしょうが、「一部の学生について勤勉だ」ということです。
小前提「ある野球部員は学生だ」の意味する所は、野球部員全体を表しているのではなく、「一部の野球部員について学生だ」ということです。
大前提と小前提の「学生」が共通概念となっていますが、大前提の一部の「ある学生」が、小前提の「学生」である一部の「ある野球部員」とは限らないわけです。
つまり、ある勤勉である「学生」とある野球部員の「学生」が必ずしも同じとは限らないということです。
したがって、この2つの前提から推論して結論「ある野球部員は勤勉だ」とすることは論理的には正しいとは言えないことが分かります。
以上の議論をまとめると、三段論法を使用する際の条件が、(1)~(5)に加えて次のモノがあることが分かります。
(6)共通概念は、少なくとも1つの前提において、全称化される
今までの推論の例を見てみると、正しい推論になる場合は、少なくとも1つの前提で、共通概念Mが全称化されているのが確認できました。
(7)2つの前提命題の述語部分に共通概念が現れる場合には、一方は肯定形、他方は否定形となる
(3.2)で、大前提「魚は泳ぐ」と小前提「マグロは泳ぐ」から推論して結論「マグロは魚だ」を導き出すことは誤りでした。2つの前提の述語部分に共通概念M「泳ぐ」が現れていますが、どちらも肯定形になっています。
大前提「犬は哺乳類だ」と小前提「シロは哺乳類ではない」から結論「シロは犬ではない」と導くのは推論として正しいです。2つの前提の述語部分が共通概念「哺乳類」ですが、大前提が肯定形で、小前提が否定形であり、推論が正しくなっています。
(8)結論命題が否定形の場合には、2つの前提命題のいずれから1つが否定形となる
再び、大前提「犬は哺乳類だ」と小前提「シロは哺乳類ではない」から結論「シロは犬ではない」と導く推論を考えてみると、結論が否定形で表されている場合に、大前提が肯定形で、小前提が否定形になっているのが確かめられます。
(9)結論命題で全称化されている、または否定されている概念は、前提命題でも全称化されている、または否定されている
(3.4)の、大前提「すべての猫は鳥類ではない」と小前提「タマは猫である」から推論して結論「タマは鳥類ではない」となる場合を見てください。結論で否定されている概念「鳥類」は、大前提でも否定されています。
また、(3.2)の、大前提「魚は泳ぐ」と小前提「マグロは泳ぐ」から推論して結論「マグロは魚だ」となる場合で考えてみます。ここで「マグロ」は、言明されていませんが、「すべてのマグロ」という意味でした。ということは、結論で全称化されている概念「マグロ」は、小前提でも全称化されていることが分かります。
これで、定言三段論法を使用する際に正しい推論となるための条件が分かりました。
表3.2.定言三段論法の成立条件
| (1)2つの前提命題と結論命題から構成される (2)どの命題も主語と述語から構成される (3)3つの概念が現れる (4)結論命題の主語と述語は、2つの前提に1回ずつ現れる (5)2つの前提命題には共通する概念が必ず1回現れて、結論命題では消える (6)共通概念は、少なくとも1つの前提において、全称化される (7)2つの前提命題の述語部分に共通概念が現れる場合には、一方は肯定形、他方は否定形となる (8)結論命題が否定形の場合には、2つの前提命題のいずれから1つが否定形となる (9)結論命題で全称化されている、または否定されている概念は、前提命題でも全称化されている、または否定されている |
2 選言三段論法
次は選言「または」が絡む三段論法を学びます。
選言三段論法は、大前提に選言の命題があり、小前提で選言の1つの命題を否定することで、結論を導くという形式の推論方法です。
論より証拠ということで、早速(3.6)を見ていきましょう。
| (3.6)次の2つの前提から得られる結論は何か。 <大前提> 太郎または花子は風邪を引いている <小前提> 太郎は風邪を引いていない [結論] よって、 |
大前提が「太郎または花子」と選言の形になっています。「太郎は風邪を引いている、または、花子は風邪を引いている」ということです。
したがって、大前提が偽である場合は、「太郎と花子の両方が風邪を引いていない」場合のみです。それ以外は、大前提は真となります。「少なくとも太郎と花子のどらか一方が風邪を引いている」ことが必要です。
そして、小前提が「太郎は風邪を引いていない」となっています。つまり、「太郎は風邪を引いている」は偽であることを示しています。
つまり、大前提が真となるためには、「太郎と花子のうち少なくとも1人は風邪を引いて」いなければならないが、小前提で「太郎は風邪を引いている」ことが否定されている状況です。
ここで「花子は風邪を引いていない」とすると、大前提が偽となってしまいます。これは大前提が真であることに反します。
それならばどう考えても、「花子は風邪を引いている」と結論づけるしかないことが分かります。
| (3.6)次の2つの前提から得られる結論は何か。 <大前提> 太郎または花子は風邪を引いている <小前提> 太郎は風邪を引いていない [結論] よって、花子は風邪を引いている |
もっと論理関係を分かりやすくするため、記号を使って単純化してみましょう。
「P」を「太郎は風邪を引いている」、「Q」を「花子は風邪を引いている」とします。
| 選言三段論法 <大前提> P または Q <小前提> P ではない [結論] よって、Q である |
大前提「P または Q」は、P と Q のうち少なくとも1つは真であることが必要です。もちろん、少なくとも1つなので、P と Q の両方真でもかまいません。
そして、小前提「P ではない」によって、P が真であることが否定されます。
そうすると、大前提から P と Q のうち少なくとも1つは真であることを満たすためには、必然的に「Q である」が真であることになります。
したがって、結論「Q である」を導くことができます。
もちろん、小前提で「Q ではない」として、結論「Pである」と導いても問題ありません。
このとき注意が必要なのは、小前提で「P ではない」と否定されていることです。
もし小前提で「P である」と肯定すると、三段論法は成り立たなくなってしまいます。
これを選言肯定の誤謬と言います。
| 選言肯定の誤謬 <大前提> PまたはQ <小前提> Pである [結論] よって、Qではない |
大前提「P または Q」は、P と Q のうち少なくとも1つは真であることが必要です。もちろん、少なくとも1つなので、P と Q の両方真でもかまいません。これは正しい選言三段論法と同じです。
そして、小前提「P である」によって、P が真であることが肯定されます。
正しい選言三段論法では、小前提で「P ではない」と否定されることで、大前提から P と Q のうち少なくとも1つは真であることを満たすためには、必然的に「Q である」が真であることになりました。
しかし、小前提で「P である」と肯定され真になると、Q が真でも偽でも大前提は真となります。
つまり、Q の真・偽判定ができないことになります。
にも係らず、結論「Q ではない」とすると、Q が真であるか偽であるかは不明なので、推論だけでは結論が正しいかどうか分かりません。
つまり、推論方法が誤っていることになります。正しい前提から正しく推論された結論は必ず正しくなることに反しています。
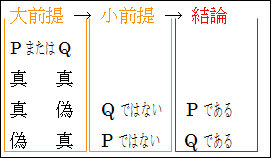
図示すると分かりやすいです。
左から右へ推論が流れていると考えてください。
大前提「P または Q」の時点では、可能性は3通りあるわけです。P も Q も偽の場合は、大前提が必ず偽になるので、最初から考えません。

正しい選言三段論法の場合、小前提で「P ではない」と否定することで、可能性は1つに絞られ、結論「Q である」が導かれます。小前提で「Q ではない」と否定しても、可能性は1つに絞られ、結論「P である」が導かれます。
しかし、選言肯定の誤謬の場合、小前提で「P である」と肯定しても、可能性は1つに絞られません。「Q である」と「Q ではない」の2つの可能性が残ります。したがって、何かしら違う前提を持ってきて推論してやらないと結論が導けないことが分かります。これは小前提で「Q である」と肯定しても同じことです。
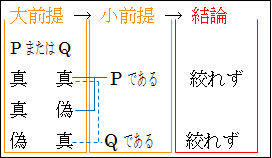
このように、選言三段論法では、前提で否定されていることに注意してください。選言肯定の誤謬は、おかしやすい間違いです。
なお、今まで話してきた選言は、少なくとも1つは真という意味で、これは包含的な場合の選言でした。
そして、選言にはもう1つ二者択一的で両立しない場合、つまり、排他的な場合もありました。「剣かコーランか」または「ライスまたはパン」のパターンがありました。
排他的な場合も、包含的な場合の選言三段論法と同じで、大前提に選言の命題があり、小前提で選言の1つの命題を否定することで、結論を導くという形式の推論方法は、当然正しくなります。
| (3.7)次の2つの前提から得られる結論は何か。 <大前提> 剣かコーランか <小前提> 剣ではない [結論] よって、 |
大前提で「剣かコーランか」と選言の命題になっています。
小前提で「剣ではない」と、選言の1つが否定されています。
これで選言三段論法による推論ができるので、結論は「コーランである」となります。要はイスラーム教に改宗することを意味します。
| (3.7)次の2つの前提から得られる結論は何か。 <大前提> 剣かコーランか <小前提> 剣ではない [結論] よって、コーランである |
では排他的な場合に選言肯定されているとどうなるでしょうか。
| (3.8)次の推論は正しいか。 <大前提> 剣かコーランか <小前提> 剣である [結論] よって、コーランではない |
大前提で「剣かコーランか」と選言の命題になっています。
小前提で「剣である」と、選言の1つが肯定されています。
この場合は、選言三段論法は使えませんでした。もし使うと、選言肯定の誤謬になってしまいます。したがって、選言三段論法としては正しい推論とはなりません、と言いたいとこですが…。
しかし、大前提の「剣かコーランか」というのは選言ではあるけど、両方真でもよいが少なくとも1つは真といった包含的な意味ではありませんでした。
最初に確認したように、大前提の「剣かコーランか」における選言は、どちらか一方のみが真という二者択一的なもので、排他的な意味でした。
通常、選言と言うとき包含的な意味を指すことが多いですが、ここでは排他的な意味です。
ということは、排他的な意味が一種の隠れた前提となり、「同時に剣とコーランを選ぶことはない」ということがあることになります。
もしこの隠れた前提を認める、つまり真と考えるならば、この推論は正しいことになります。
| (3.8)次の推論は正しいか。 <大前提> 剣かコーランか <小前提> 剣である <隠れた前提> 同時に剣とコーランを選ぶことはない [結論] よって、コーランではない |
隠れた前提より、「剣とコーランの両方が同時に選ばれることはない」のだから、小前提で「剣である」と肯定すると、残りのコーランは必ず選ばれなくなるからです。
ただし、3つの前提から結論が導かれているので、もうこれは厳密な意味での三段論法にはなっていませんが。
以上のことをまとめると、
選言三段論法は、選言が包含的であろうと排他的であろうと、常に成り立ちます。
そして、選言肯定の誤謬は、選言が包含的な場合に生じます。
しかしながら、一見すると選言三段論法の形式をとっているのに、選言肯定の誤謬が生じないことがあります。それは選言が排他的な場合です。
選言は包含的なモノと考えるのが一般的なので、推論の形式を常に正しくしておくためには、選言が排他的な場合は明示して前提の1つにしておくのがよいです。
前提の1つとして明示されていないと、隠れた前提として処理する必要があります。
| 選言三段論法 <大前提> PまたはQ <小前提> Pではない [結論] よって、Qである ・選言肯定の誤謬(包含的場合) <大前提> PまたはQ <小前提> Pである [結論] よって、Qではない ・選言肯定の誤謬(排他的場合) 隠れた前提を見つけ出す <大前提> PまたはQ <小前提> Pである <隠れた前提> PとQは両立しない [結論] よって、Qではない |
人と議論しているときに、相手が選言三段論法の選言肯定の誤謬をしていたら、隠れた前提があるのか考えてみるとよいでしょう。
その隠れた前提がどうも真ではないと判断できたら、その推論は正しくないのから、結論は妥当ではないことを指摘するとよいでしょう。
もちろん、隠れた前提が正しくないときや明示しておいた方がよいときには指摘して、話が誤った方向に進むのを止めるのはいいこです。
が、議論の中では隠れた前提を明示せずとも、分かり切っていたり共通了解があるのに、最初から推論形式にばかりこだわって、逐一選言肯定の誤謬を指摘して話を止めていたら鬱陶しがられるので、気を付けてください。
3 仮言三段論法
続いて、仮言三段論法を学びます。
仮言三段論法は、条件法「ならば」と三段論法を用いて推論していくものです。
条件法の命題「P ならば Q」は、P と仮定して Q が導けるということを表しており、この意味で仮言つまり仮に言うということです。
それでは実際に例を見ていきましょう。
| (3.9)次の2つの前提から得られる結論は何か。 <大前提> 雨が降るならば、試合は中止だ <小前提> 試合が中止ならば、入場料は入らない [結論] よって、 |
これは論理の流れが非常に分かりやすいかと思います。
大前提で「雨が降るならば」「試合は中止だ」となっています。
そして、小前提で「試合が中止ならば」「入場料が入らない」となっています。
このことから、大前提との小前提に共通する「試合は中止だ」によって、大前提の前件「雨が降る」から、小前提の後件「入場料が入らない」を導くことができます。
したがって、結論は「雨が降るならば、入場料は入らない」となります。
| (3.9)次の2つの前提から得られる結論は何か。 <大前提> 雨が降るならば、試合は中止だ <小前提> 試合が中止ならば、入場料は入らない [結論] よって、雨が降るならば、入場料は入らない 雨が降る ⇒ 試合は中止 ⇒ 入場料は入らない |
一番左に位置する「雨が降る」から、中央に位置する「試合は中止だ」を経由して、一番右に位置する「入場料は入らない」まで、右向きの矢印(⇒)で結べているのも視覚的に確認できます。
論理の流れがを明確にするために記号化してみます。
「雨が降る」を「P」、「試合が中止だ」を「Q」、「入場料は入らない」を「R」とします。
すると、大前提は「P ⇒ Q」、小前提は「Q ⇒ R」、結論は「P ⇒ R」となります。
| (3.9.1) <大前提> P ⇒ Q <小前提> Q ⇒ R [結論] よって、P ⇒ R P ⇒ Q ⇒ R |
P から、Q を経由して、R まで、⇒ で流れて行けるのが分かります。
これが、仮言三段論法の基本的な形式になります。
| 仮言三段論法 <大前提> P ⇒ Q <小前提> Q ⇒ R [結論] よって、P ⇒ R P ⇒ Q ⇒ R |
たまに、2つの前提「P ⇒ Q」と「R ⇒ Q」から結論「P ⇒ R」を導く人がいますが、これは仮言三段論法としては誤りです。
2つの前提「P ⇒ Q」と「R ⇒ Q」ではどちらも後件に「Q」があるため、「P ⇒ Q ⇒ R」といった一本のルートになり得ません。
| 犯しやすい仮言三段論法の誤り <前提> P ⇒ Q <前提> R ⇒ Q [結論] よって、P ⇒ R → 正しくは、P または R ⇒ Q |
例えば、(3.10)を見てみましょう。
| (3.10)次の2つの前提から得られる結論は何か。 <前提> 雨が降るならば、試合は中止だ <前提> 入場料が入らないならば、試合は中止だ [結論] よって、 |
2つの前提を「雨が降るならば、試合は中止だ」と「入場料が入らないならば、試合は中止だ」で考えてみましょう。
これから推論して得られる結論は、「雨が降るか、または、入場料が入らないならば、試合は中止だ」といったものになります。これは、「試合が中止である」場合がどのような場合かを表しているに過ぎず、(3.9)のように、「雨が降るならば、入場料が入らない」といったことは導けません。
| (3.10)次の2つの前提から得られる結論は何か。 <前提> 雨が降るならば、試合は中止だ <前提> 入場料が入らないならば、試合は中止だ [結論] よって、雨が降るか、または、入場料が入らないならば、試合は中止だ |
論理の流れが見やすいように、記号化してみます。
「雨が降る」を「P」、「試合は中止だ」を「Q」、「入場料が入らない」を「R」とすると、
| (3.10.1) <前提> P ⇒ Q <前提> R ⇒ Q [結論] よって、P または R ⇒ Q ×P ⇒ Q ⇒ R |
のようになります。P と R が条件として並立しているのであって、決して「P ⇒ Q ⇒ R」ではありません。条件法を見るとすぐに、仮言三段論法と考えて間違った推論をしないようにしましょう。
正しい仮言三段論法では、「P ⇒ Q ⇒ R」という論理の流れが一本道になっているものと、「P ⇒ Q、R ⇒ Q」という「P」と「R」から出発する2つの論理の流れが1つの「Q」にたどり着く形を混同しないように気をつてください。
なお、仮言三段論法は条件法を用いているので、第2章 推論方法の基礎 5 条件法もよく復習しておいてください。
4 まとめ
このように、2つの前提から結論を導く推論形式が三段論法です。
そして、三段論法の種類として、大きく別けて、定言・選言・仮言と3つの場合を見てきました。
分かりやすいように、定言三段論法なら定言のみの前提で、仮言三段論法なら仮言のみの前提で構成しておきましたが、実際には、定言・選言・仮言が混じりながら使用されることが多いです。
例えば、第2章 推論方法の基礎 5 条件法で見た前件肯定規則や後件否定規則は、大前提が仮言でしたが、小前提は定言で構成されていました。
今まで見てきた例は簡単な内容や論理なので、わざわざ推論形式を学ぶ必要も感じないかもしれませんが、複雑な事象を整理するのに役立つ基礎です。また同時に、色々な推論の雛形的な位置づけになります。各三段論法の基本的な型をしっかりと押えて、正しい推論方法の知識を活用しながら、論理的に思考できるようにしてください。
推論方法の基礎と典型的で有名な三段論法を学んだので、次からより高度な推論方法を学んでいくことにします。
前頁:第2章 推論方法の基礎
ページトップへ:第3章 三段論法
次頁:第4章 演繹法