前頁 |▼| 次頁
第18章 設定型の問題と創造型の問題
前章までは論理ツリーの説明しました。「設定型」の問題と「創造型」の問題も論理ツリー、特に how ツリーを用いることになります。
両問題ともに、主に how ツリーを使うことになるので、how ツリーの繰り返しの説明はしませんが、それぞれの注意点と応用について触れてきます。
| 目次 |
| 1 「設定型」の問題 2 創造的思考 3 「創造型」の問題 4 まとめ テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 「設定型」の問題
前章までは、論理ツリーの使い方を説明してきました。
構造や概念の整理・分析のための what ツリー。原因分析のための why ツリー。解決策を考えるための how ツリー。この3つがありました。
問題の類型で言えば、「発生型」の問題への対処法を説明しました。
「発生型」の問題は、単発的に現れて、1つに特定できる「困った事態」でした。why ツリーは、この「発生型」の問題の原因を分析するのに役立ちました。
そして、残る問題の類型は、「構造型」、「現象型」、「設定型」、「創造型」の4つです。
そこで、論理ツリー、特に how ツリーを主に使う「設定型」の問題と「創造型」の問題について説明します。
改めて確認します。
how ツリーは、課題を解決するためにどのような方法があるかを考えるための論理ツリーです。しかし、how ツリーを作る前にやるべきことがありました。それは、問題の本質的な原因を明らかにして、それを解決すべき課題として課題化することでした。
図18.1.発生型の問題の解決の過程 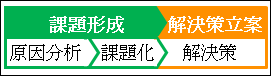
「発生型」の問題を思い返してみてください。
確かに、まず why ツリーを使って本質的な原因を特定してから、それを課題化して、次に how ツリーで解決策を考えるという手順でした。
図18.1.発生型の問題の解決の過程 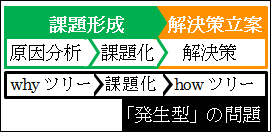
その過程で、理想の状態や現実の状態を分析して明らかにしていました。
図18.1.発生型の問題の解決の過程 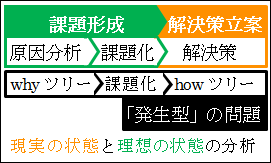
では、「設定型」の問題ではどうなるでしょうか。
皆さんの予想通り、基本的な流れは同じですが、少し注意が必要です。「設定型」の問題の特徴を確認しながら注意点を見て行きましょう。
まず、「設定型」の問題とは、実現すべき課題や、達成すべき課題を設定する問題です。
ですから、「設定型」の問題は、なぜ「困った事態」が起きているのか、その本質的な原因は何なのか、といったことを考えずに、何かをしたいと考えることから始まる場合が多いです。
図18.2.設定型の問題の解決の過程 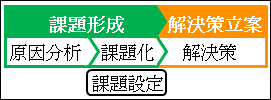
例えば、「志望校に受かる」という課題を設定したとします。
「志望校に落ちる」という事態が発生することが簡単に予想される場合には、それは「困った事態」だと言えるかもしれません。
が、しかし、「志望校に受かる」という課題は、「困った事態」を解消するためと言うよりは、「志望校に受かる」こと自体を目標として設定していると言えます。
このように、実現すべき課題や、達成すべき課題を設定する「設定型」の問題の場合は、原因分析よりも前に、ある程度明確に解決すべき目標が設定されていることが多いことが分かります。
そうすると、目標たる解決すべき課題が明確になっているだけに、ついつい「志望校に受かる」ためには「どうやって?」と、いきなり考えてしまいやすいです。
つまり、原因分析をせずに、目標として設定された課題を達成するための方法を考え始めてしまいがちだということです。
図18.2.設定型の問題の解決の過程 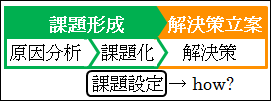
それでは、「志望校に受かる」という目標・課題を設定して、すぐに「どうやって?」how? と解決策を考えてみてください。
おそらく、どのような解決策が効果的で効率的なのか判断がつかないはずです。さらには、思考が発散して収拾がつかなくなっていくはずです。
つまり、「志望校に受かる」ための方法は色々ありますが、何の準備なしに考えてみても、効果的ではないことが分かります。
なぜなら、「志望校に受かる」と課題を設定しただけでは、現実の状態や理想の状態がどのようなものなのかが分、具体的に分かりません。
それゆえに、前提条件や制約条件が不明のままなので、具体的な状況に適した解決策で、「実効性」があり「実現可能性」がある解決策が何なのかが、まったく分かりません。
図18.2.設定型の問題の解決の過程 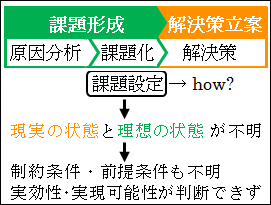
したがって、「設定型」の問題でも、目標や課題が明らかだからといって、いきなり how?「どうやって?」と問うのではなく、現実の状態を分析して、「現実の状態がどうなっているのか」を明らかにして、「課題や目標が達成されたとはどういう状態なのか」を最初にしっかりと考えておく必要があります。
図18.2.設定型の問題の解決の過程 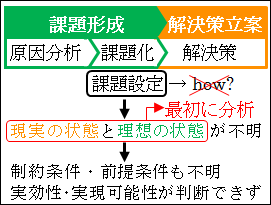
これは、結局、問題の認識の重要性と同じことを言っていることになります。図14.4.問題の認識を見てください。
図14.4.問題の認識 画像クリックで拡大 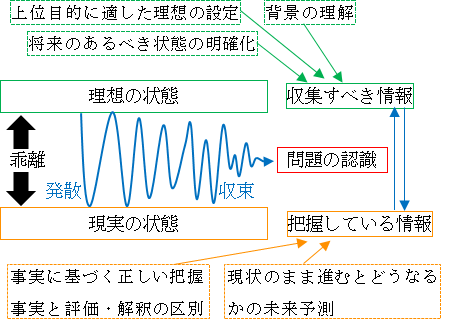
理想の状態が目標です。
現実の状態が、文字通り、今自分が置かれている状況です。
理想と現実の乖離、要はギャップが存在するから、理想の状態が目標になります。
そして、現実の状態を何とかして理想の状態に近づけようとすることが課題となるわけです。
こうした理由から、「志望校に受かる」という課題を設定して、すぐに解決策を考え出すのは悪手なのが理解できます。
ここまでの話をまとめておきます。
目標や課題を設定することから始まる場合が多い「設定型」の問題は、 how ツリーを使って解決策を考え出す前に、
理想の状態はどのようなものなのかを具体化しておくこと、
現実の状態がどうなっているのかを分析しておくこと、
理想の状態と現実の状態の乖離を具体的にしておくこと、
この3つが大切です。
なお、理想と現実の状態と両者の乖離は、発散と収束を繰り返しながら行ったり来たりして徐々に具体化されていくことは忘れないでください。
まず、目標や課題を設定しただけでは、理想の状態が具体的ではないです。
これでは近づけるべき理想の状態が何なのかが分からないので、何をしてもある意味では理想の状態に近づけたと言えます。ですから、「課題や目標が達成されたとはどういう状態なのか」を具体的にする必要があります。
また、目標や課題を設定するだけでは、現実の状態がどのような状況にあるのかも分かりません。
もちろん、現実の状態が分からないと、理想の状態からどれだけ離れているのかも分かりません。そうすると、何をすれば課題が解決できるのかが分かりません。ですから、現実の状態を分析する必要があります。
図18.3.設定型の問題の明確化 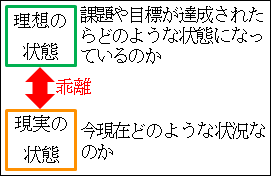
理想の状態と現実の状態とが具体的になって、両者の乖離が明確になった段階で、やっと how ツリーを使って解決策を考え出す段階になります。
how ツリー作成段階になれば、後は前章でやったように、前提条件や制約条件を意識しながら解決策を考え出していけばいいことになります。
改めて、「志望校に受かる」という例を使って考えてみます。
目標、あるいは、実現すべき課題、理想の状態として「志望校に受かる」ことを設定したとします。
目標たる理想の状態は、「志望校に受かる」ことです。
具体的には、「合格点をとる」、あるいは、「合格基準を満たす」ことと言えます。
このように、「受験科目それぞれで必要な点数」等をどんどん具体化していきます。
「受験科目1で X1 点」「受験科目2で X2 点」「受験科目3で X3 点」と具体化でき、「合格に必要な受験科目の合計点は X である」と具体化できます。
図18.4.志望校合格の課題の明確化 
現実の状態の分析はどうでしょうか。
現状を分析するとしたら、「自分の各教科の成績」や「現在の勉強量」など色々要素が挙げられます。
理想の状態である受験科目の点数に関して調べれば、「受験科目1で Y1 点」「受験科目2で Y2 点」「受験科目3で Y3 点」と具体化でき、「現在の自分の受験科目の合計点は Y である」と具体化できます。
「現在の勉強時間・量」からは、日常の生活でどれだけの時間を勉強につぎこんでいるのかや、自分の処理能力がどれだけのものなのかといったことが分析できるはずです。
とりあえず、課題に関係ありそうなことをどんどん分析して行きます。
図18.4.志望校合格の課題の明確化 
理想の状態と現実の状態が明らかになると、両者の乖離・ギャップが明らかになります。
「志望校に受かる」という目標・課題のためには、「受験科目の合計点で X-Y 点上げる必要がある」。
各科目で言えば、「受験科目1で X1-Y1 点」、「受験科目2で X2-Y2 点」、「受験科目3で X3-Y3 点」、それぞれ上げる必要がある。
他にも、前提条件や制約条件として、「勉強時間はこれ以上増やせるか否か」や「得意科目や苦手科目の有無」など色々と設定できるはずです。
図18.4.志望校合格の課題の明確化 
こうして、最初に設定された「志望校に受かる」という課題が具体的になったら、how ツリーを使って、どういった解決策の方向があるのかを考えて行けばいいです。
「得意科目を中心に伸ばすべきなのか」、「苦手科目をしっかりと克服すべきなのか」といった視点から解決策を考えるのもいいでしょう。
または、「勉強量をできるだけ増やしていくべきか」、「勉強量を変えずにいくべきなのか」という視点もあるでしょう。
他にも、カネやコネがあるのならそれを使うための解決策の方向を検討してみるのもいいでしょう。
最後のは冗談ですよ。
ともかく、「志望校に受かる」という課題を設定して、すぐに how ツリーを作成するよりも効果的で効率的、あるいは、「実効性」があって「実現可能性」のある解決策が考えられるはずです。
以上のように、「設定型」の問題であっても、how ツリーを作る前に、しっかりと現実の状態と理想の状態を分析しておく必要があることに注意してください。
2 創造的思考
続いて、「創造型」の問題と how ツリーの関係の説明に移る前に、論理的思考を踏まえた創造的思考について少し触れおきたいと思います。
復習ですが、創造的思考 creative thinking は、制約条件を無視したり変更したりして今までに無かったような考えを生み出す ための思考でした。
制約条件は、当事者が変更できない条件でした。
制約条件を無視すればとんでもない方向に思考が流されていくかもしれないので、制約条件は常に意識しておかないといけません。制約条件があることで、課題解決から外れずに効果的で効率的な解決策を考えることができました。
そして、創造的思考の中で、すべての制約条件を外して考える方法をゼロベース思考と言いました。
創造的思考は、今までになかったような何か新しいことを考え出したりするときに使います。
しかし、創造的思考は、何か新しいことを考え出す以外にも使い道があります。
行き詰まった思考、硬直的になった思考を打ち破るのにも役立ちます。
つまり、今までになかったような新しいこととまではいかなくても、制約条件や前提となっている条件を守りながら、論理的に how ツリーを作っているときにも創造的思考が利用できるということです。
「創造型」の問題に入る前に、それに縛られない創造的思考の利用法について話したいと思います。
ずっと説明して来たことですが、how ツリーでは、論理的思考を使いながら、枠組みを適切に設定して解決策を考え出しています。
このとき、「どうも良い案が思いつかない」といったのように、考えに行き詰まることがあります。そういうときは、枠組みを変える等して考え方を変えたりしながら、必死に解決策を絞り出そうとするものです。
しかし、意図的に考え方を変えようとしてもそう簡単には行きません。そもそも、簡単に考え方を変えられないからこそ、行き詰まっているのだとも言えます。長い時間考え事をしていると、どうしても思考の方向性が凝り固まりがちです。
この行き詰まった感覚は、誰もが経験したことがあることだと思います。
論理的思考を使っているときに思考が硬直化していく様を分かりやすく図解してみます。
○が、有り得る解決策です。何の制約条件や前提条件もなければ、この中から自由に選べます。
図18.5.創造的思考の概念図 
しかし、現実には、制約条件や前提条件があります。
そして、こうした条件によって、各解決策に「実効性」や「実現可能性」があるかが決まってきます。
そこで、制約条件や前提条件で使えない解決策を緑色で塗りつぶします。
実線で縁をとっているのが当事者に変更不可能な制約条件です。
縁がないのが当事者に変更がある程度は可能な前提条件です。自由度があるといってもいいでしょう。
図18.5.創造的思考の概念図 
このように、複数の制約条件や前提条件によって、○の数が絞り込まれます。
今、○で残っているものが、制約条件や前提条件から、実行が可能で、課題解決に効果があるものです。
この中から、解決策を選ぶことになります。
後の説明で区別しやすくするために、○を赤色で塗りつぶしておきます。
図18.5.創造的思考の概念図 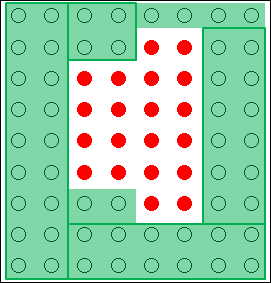
と言っても、現実には、●が目の前に転がっているわけではなく、また、●をすぐさま思いつくわけではありません。色々な枠組みを使って解決策を認識して自分で考え出さないといけません。
枠組みによって認識する解決策を黄色の枠で囲ってみます。
図18.5.創造的思考の概念図 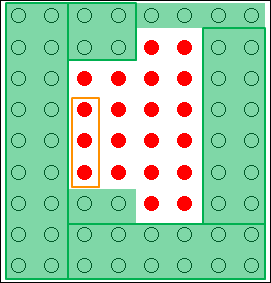
枠組みは、自分で一から作る場合もあれば、既にあるものを使る場合もあります。いずれにしろ、MECE に(ダブりなくモレなく)考えたり、論理的に考えるのに非常に有益でした。
しかし、実際に枠組みを作ってみると分かると思いますが、都合よく制約条件や前提条件の中にある解決案すべてを漏れなく考えるのは、非常に難しいです。何回か枠組みを変えても、つまり、考え方を変えても、すべての解決策を思いつくことは難しいです。
図18.5.創造的思考の概念図 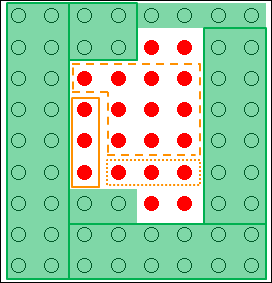
こうなると、自分の持っている枠組みも尽きて、発想を変えようにも難しく、考えに行き詰まった状態になったと言えます。
そこで、敢えて制約条件や前提条件を一部変更し、考え直すことで、発想の転換を試みます。
つまり、思考の方向性を縛っていた条件を変更することで、思考を発散させ、発想の転換を図ろうということです。
方法として、条件を強化することと条件を緩和することの2通りあります。
変更対象が、変更不可能な制約条件と変更可能な前提条件の2通りあります。
したがって、方法が、2×2=4通りあることになります。
これに加えて、まったくの0から考えるゼロベース思考があるので、計5通りの方法が存在します。これを順に見て行きます。
まず、制約条件の変更からです。
制約条件の一部を変えることは、今まで思考を縛り付けていた条件が変わることを意味します。そうすると、思考の縛りが変わることになるので、何か新しいことを思いつく可能性が出てきます。
制約条件の一部を変える方法は、主に2通りあります。
1つ目は制約条件の緩和です。
ある制約条件を無くしたり、緩くしたりすることで、制約条件を変えます。
そうすると、条件が緩くなるので、解決策をより幅広く考えやすくなります。
図の制約条件の1つを外してみます。緑色で塗りつぶした部分の一部を元に戻します。
図18.6.創造的思考の概念図―制約条件の緩和 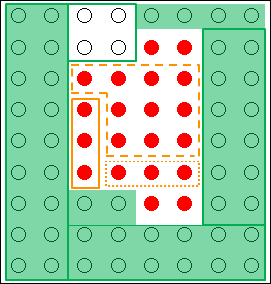
物の見え方が変わり、視野が広がるので、考え付かなかった解決策が思いつくかもしれません。
例えば、二重線の黄色の枠が制約条件を緩和することで考え付いた枠組みです。●を新しく含んだものです。
図18.6.創造的思考の概念図―制約条件の緩和 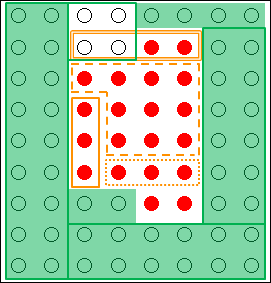
ただし、課題の解決に「実効性」や「実現可能性」のない解決策である○まで含まれているので、最終的には、この2つの○は後で外して考える必要がありますが。
とにかく、行き詰まって考え出せなかった●を2つ思いつくことができました。
2つ目は制約条件の強化です。
ある制約条件を新しく設けたり、厳しくしたりすることで、制約条件を変えます。
そうすると、条件が厳しくなるので、視野が狭くなり、新しい気付きが生じる可能性が出てきます。
要は、「灯台下暗し」みたいな感じです。探し物をしていて見つからないと思ったら、すぐそこの目の前にあったみたいな感じです。敢えて条件を厳しくしてみて思考をガチガチに縛ってみることで、ピンポイントに新しい発想を得る試みです。
図の制約条件を厳しくしてみます。緑色で塗りつぶす部分を増やします。
図18.7.創造的思考の概念図―制約条件の強化 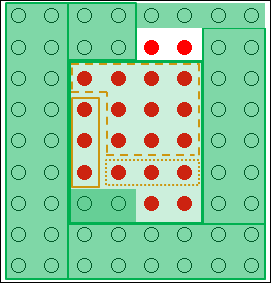
そうすると、嫌でも2つの●に考えが行くようになります。
図18.7.創造的思考の概念図―制約条件の強化 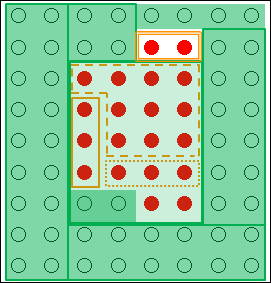
これで、新しい枠組みを設定でき、●を思いつくことができました。
制約条件を一部変更する方法以外にも、変更可能な条件を変えてみることで、発想の転換を促す方法があります。
いわゆる自由度を変更することです。
制約条件は当事者が変更することできませんが、前提条件の中には、変更の幅に限度があるにしても、一応は当事者が変更できるものがあります。
例えば、予算や期間、人員は、最大値が決まっていても、最大値以内なら多くしたり少なくしたりできます。もしかしたら、頑張れば最大値を変えることができる場合もあります。
このように変更可能な前提条件を変えることで、自由度を変更することになります。
自由度を変える方法も、主に2通りあります。
1つ目は自由度の拡大です。
ある前提条件を無くしたり、緩くしたりすることで、自由度を変えます。そうすると、条件が緩くなるので、解決策をより幅広く考えやすくなります。
制約条件を緩和したように、自由度を広げてみます。緑色で塗りつぶしていた部分を一部元に戻します。
図18.8.創造的思考の概念図―自由度の拡大 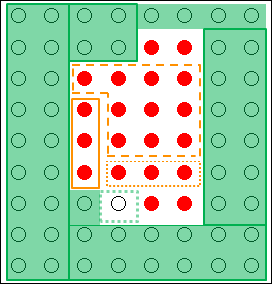
こうすることで、新しく●を思いつくことができます。もちろん、新しく含まれた○は、課題の解決に「実効性」や「実現可能性」のないので外しておく必要があります。
図18.8.創造的思考の概念図―自由度の拡大 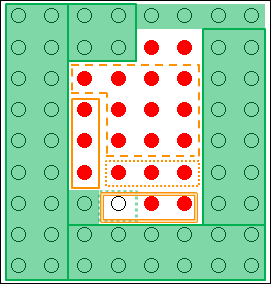
2つ目は自由度の縮小です。
ある前提条件を新しく設けたり、厳しくしたりすることで、自由度を変えます。そうすると、条件が厳しくなるので、何かしらの新しい気付きがあるかもしれません。
制約条件を厳しくしたように、自由度を縮小してみます。緑色で新しく塗りつぶす部分を増やします。
図18.9.創造的思考の概念図―自由度の縮小 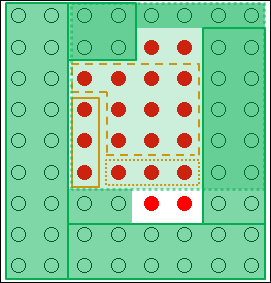
そうすると、嫌でも2つの●に考えが行くようになります。
図18.9.創造的思考の概念図―自由度の縮小 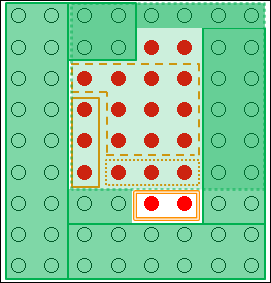
これで新しい枠組みを設定でき、●を思いつくことができました。
このように、制約条件や自由度を変更することで、考えに行き詰まった状況を打破できるかもしれません。
そして、制約条件を変えたり自由度を変えたりすることを極端に推し進めたのが、ゼロベース思考 zero-base thinking です。
ゼロベース思考では、すべての制約条件を外して考えることになります。特別に条件に縛りを設けずに、思いつくままにどんどん考えを出していきます。
イメージとしては、白紙で考えることになります。
繰り返しになりますが、ゼロベース思考では、非現実的だが極端な場合どうなるかといったことを始めとして、すべての制約条件を外して考えてみることが大切です。
制約条件であろうが関係なしに、思考を縛り得る様々な条件を取っ払って解決策を考えます。
したがって、ゼロベース思考では、当然ながら、常識に照らせば荒唐無稽に思えるような案が大量に生まれます。その量は、制約条件や自由度を一部変更するだけよりも圧倒的です。
ですが、ゼロベース思考では、問題の見方を変えて、とにかく構想を絞り出すことが狙いなので、問題ありません。
このように、創造的思考では、制約条件の変更、自由度の変更、ゼロベース思考といった方法が役に立ちます。論理的思考で行き詰まった際には、使ってみてください。
創造的思考の最後に、注意点として、制約条件を変更したり、自由度を変更したりすれば、自ずと「実効性」や「実現可能性」の面で難が生じやすくなることです。
ちょっと考えれば分かると思いますが、制約条件や自由度は、論理的思考で現実の状態や理想の状態を具体化したり、定義したりするための前提となっています。これを意図的に変更するのだから、現実の状態や理想の状態からズレが生じる可能性があります。すべての条件を取っ払ってしまうゼロベース思考になると、そのズレは更にもっと大きくなります。
図で言えば、創造的思考を使って考えると、「実効性」や「実現可能性」のある●だけではなく、「実効性」や「実現可能性」のない○が含まれてしまうことからも、理解できます。
したがって、創造的思考で考え出した案は、他の場合よりも、本当に「実効性」と「実現可能性」があるかの仮説検証をしっかりする必要があることに注意してください。
このように、論理的思考だけでは視野が狭くなりがちなところ、創造的思考が視野を広げたり、新しい考えを生み出すのを手助けしてくれます。
逆に、創造的思考だけでは、「実効性」も「実現可能性」もあるかないか分からないところを、論理的思考によってそれがあるかないかを検討することができます。
3 「創造型」の問題
創造的思考の実行法や注意点が分かったところで、「創造型」の問題の話に移ります。
と言っても、この講義では論理的思考による問題解決を目的としているので、「創造型」の問題については実例を使って論理ツリーを組み立てたりしません。
もっと正直に言えば、既存の知識を紹介するのではなく、この場で創造的思考を用いて、創造的 creative な解決策とか事業とかを紹介することが、私にはできないからでもあります。少しくらい何か付け加えて独創的に見せることはできても、まるで今まで考えられもしなかったようなことを披露するほど、私は創造的ではありませんから。
さて、「創造型」の問題は、新たなことを創出するような創造的な課題を設定する問題でした。どのような方向で今までに無かったような創造的なことを生み出すのかを定めることが大切になります。
いくら今までになかった新たなことを生み出すといっても、何か目的があるはずなので、その目的から逸脱しないように方向性はある程度定めておかないといけません。
目的から離れた解決策が無用の長物であったのと同じで、独創的なものだから良いわけではありません。独創的であり、今までにない程に目的をよりよく達成してくれるから良いことを忘れないでください。
そして、こうした創造的な考えを生み出す場合には、論理的思考も大切ですが、創造的思考が重要になってきます。
「設定型」の問題と同様に、色々な事柄を調査して検討して論理的に物事を考える必要がありますが、そこから更に、制約条件や前提条件をある程度取っ払って創造的に考えることも大切になります。つまり、「設定型」の問題よりも創造的思考の役割が大きくなります。
「創造型」の問題では、新しいことを始めるのが主になるので、今までにあった事例、つまり、前例がなかったり少なかったりすることが普通です。
前例がなかったり、少なかったりするということは、上手く行った事例や失敗した事例が少ないことになります。そうすると、上手く行った場合の状況や失敗した場合の状況が、あまり明らかではないことを意味します。
例えば、ある事業を始めて、上手く行った場合に、条件 A があったとします。また、他にも数少ない事例を調べてみると、条件 A があったとします。
このとき、条件 A が、上手く行くための必須の条件だと考えてしまいがちです。
しかし、実は条件 A がたまたま存在しているだけで、条件 A がなくても上手くいっていたのかもしれません。
事例が少ないので、条件 A がない場合がたまたま見つかっていないだけかもしれません。
条件 A と結果 B が同時に現れると、「A ならば B」のように、因果関係等を安易に見つけ出そうとしてしまうのが、人間の習性です。
数少ない事例を安易に一般化するのは、早まった一般化という誤謬でした。
また、人間は類似した事例を見つけると、同じような方法で解決できるとも考えがちです。
自分が取り組もうとしている課題と調べている事例が本当に同じなのか、と疑うことも必要です。世の中には、似たような事例だけど微妙に異なっているものでが多数あります。その微妙な違いが、現実には結果を大きく左右したりするものです。
誤った類比も誤謬の1つでした。
このように、先例がないからこそ、自分の頭で1から考えることが大切になります。したがって、「創造型」の問題は、目的達成志向を持ちながらも、臨機応変に柔軟に考えることが大切です。
何か新しいことをするとき、制約条件や前提条件を絶対のものと考えて思考の幅を狭めても良い考えが生まれ難いです。制約条件に縛られずに幅広い観点から考えたり、自由度を変えてみて色々な視点から考えてみることが大切になります。そして、制約条件と思っているものが、実はそうではなかったということも十分あります。
ですから、創造的思考によって、自由な発想で、今までの先例に縛られずに考えることが大切になります。
その一方で、人間は偏見と誤謬に満ち溢れていることを自覚することも大切です。
人間は、自分に都合が良いように物事を考える癖があります。そして、自分に都合が良い様に物事を事実であったり、真実であったりと見ようとします。そうした習性があることを弁えて、自由な発想が自分勝手な独り善がりな発想に陥らないように心掛けておかないといけません。
「創造型」 の問題は、難しい課題ですが、非常に面白いものです。実行するかは別としても、楽しみにながら色々と考えてみるといいでしょう。
4 まとめ
「設定型」の問題も「創造型」の問題も、論理ツリーの how を主に使います。
しかし、実際に how ツリーの作成に取り掛かる前に、現実の状態と理想の状態の分析して把握することが必要でした。それを踏まえたうえで how ツリーを作成しないとけません。
「発生型」の問題で本質的原因を分析した後に解決策を考える場合でも、論理的思考以外にも創造的思考が必要になることもあります。「設定型」の問題でもそれは同じです。そして、「創造型」の問題では、いっそう創造的思考が求められることになります。
ただし、創造的思考で考え出された解決策は、論理的思考に比べると、実際に解決しなければならないことと離れている確率が高くなっています。ですから、他の場合よりも、構想たる案や仮説を実現する手段や計画をしっかりと考えておかないといけません。
いずれにしろ、創造的思考 creative thinking は、「創造型」の問題で大いに活躍しますが、それ以外の解決策を考えるときにも有効ですので、0か1かではなく、少しでも使えるように、常識に縛られずに自由に発想しながら訓練してみてください。
前頁:第17章 論理ツリー ― how ツリー―
ページトップへ:第18章 設定型の問題と創造型の問題
次頁:第19章 因果関係図