前頁 |▼| 次頁
第4章 演繹法
推論方法の基礎として三段論法を学びましたが、この三段論法は演繹法を一般化したものと言えます。
そこで演繹法とは何なのか。どのような推論方法なのかについて考えていきたいと思います。
| 目次 |
| 1 定義 2 一般・普遍・抽象と個別・特殊・具体 3 演繹法の構造 4 相対的と絶対的 テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 定義
演繹法とは、一般的・普遍的・抽象的な命題や法則を前提として、その前提から、より個別的・特殊的・具体的な結論を導く推論方法である
と定義されます。ちなみに英語では deduction と言います。また、deductive reasoning と言うこともあり、日本語では演繹法的推論や演繹的推論になります。
呼び方は様々にありますが、ここでは演繹法と呼ことを基本とします。
この演繹法を単純化したのが、三段論法と言えます。
演繹法は、アリストテレス以来ずっと哲学者やキリスト教の教義を研究する人である神学者等によって利用されてきました。
そして、17世紀前半に活躍したフランスの哲学者デカルトが、演繹法での推論を厳密な学問で使用できるように整理しました。
こうしたデカルトの思想の流れをフランス合理論と呼びます。
それでは演繹法について分析していきましょう。
| (4.1)演繹法の特徴 <大前提> 魚は卵を産む <小前提> 鮭は魚である [結論] よって、鮭は卵を産む |
三段論法によって推論されています。
大前提の「魚は卵を産む」とは、「すべての M は P である」の形をしています。
小前提の「鮭は魚である」とは、「S は M である」の形をしています。「S」は「鮭」なので、「M」の「魚」に対して特称的な意味合い、つまり「ある魚」という意味合いを持ちます。
結論の「鮭は卵を産む」とは、「S は P である」の形をしています。
定言三段論法として正しく推論されていることが確認できました。
推論が正しいことが確認できたので、演繹法がどういうことかを確認していきます。
もう一度確認しますが、演繹法は、一般的・普遍的・抽象的な命題や法則を前提として、その前提から、より個別的・特殊的・具体的な結論を推論するものです。
まず一般的とは、全体的に当てはまるといった意味で用いられます。
それに対して、個別的とは、それぞれ別々に扱うといった意味で用いられます。
大前提の「魚は卵を産む」と結論の「鮭は卵を産む」を比較すると、どちらがより一般的なことを述べているかが明らかになります。
「魚」と「鮭」ではどちらか一般的かと言えば、「魚」に決まっています。これは小前提の「鮭は魚である」からも確認できます。
とすると、「鮭」は、一般的なモノである「魚」に比べて、より個別的のモノと言えます。
このことから確かに、より一般的な命題である大前提「魚は卵を産む」を前提として、その前提からより個別的な結論を推論して導いていることが分かります。
これが演繹法の基本的な考え方と推論方法です。
2 一般・普遍・抽象と個別・特殊・具体
演繹法の定義で、一般的・普遍的・抽象的という言葉と個別的・特殊的・具体的という言葉を特に気にせず使いましたが、これらの言葉の意味を確認しておきます。
議論や学問を行う上で、この言葉は非常に重要になってくるからです。
実は、これは次のように類義語と対義語の組み合わせになっています。
|
物事が広く当てはまったり、物事について全体的な話をしている場合には、「一般的に言って」等の枕詞を使いますね。
「一般的・普遍的・抽象的」の3つは、細かく見れば意味が微妙に異なりますが、大きく捉えれば、広い話や全体的な話をしているという点で非常に似た言葉です。
例えば、「日本人は物静かだ」というのは日本人全体に当てはまる広い命題になります。
「広い」の反対は「狭い」であり、「全体的な」の反対は「部分的な」です。
このことから分かる通り、「個別的・特殊的・具体的」の3つも、細かく見れば意味は微妙に違いますが、大きく捉えれば、狭い話や部分的な話をしている点で似た言葉となっています。
「日本人は物静かだ」という命題と比べて、「太郎は物静かだ」というのは、日本人の中の1人の個人の話をしているので、狭い部分的な命題になっています。
これらの言葉の関係と違いを明確にしておきたいので、これからする説明は若干くどくなりますが、(4.1)の「魚」と「鮭」の関係から見てみましょう。
| (4.1)演繹法の特徴 <大前提> 魚は卵を産む <小前提> 鮭は魚である [結論] よって、鮭は卵を産む |
大前提の「魚は卵を産む」と結論の「鮭は卵を産む」というのを比較します。
小前提の「鮭は魚である」からも分かる通り、「鮭」は「魚」の一種です。
先ず、「一般的」と「個別的」という対の語について考えてみます。
「一般的」とは、広く全体的に当てはまるさまです。
「個別的」とは、それぞれ別々に扱うさまです。
大前提の「魚は卵を産む」では、「魚」には「鮭」も含む色々な魚があり、「魚」について広く全体的に当てはまるコトを述べているのが分かります。
これに対して、結論の「鮭は卵を産む」では、「魚」の中でも「鮭」という種類の魚についてのみ述べています。
つまり、「鮭」という「魚」の中の一部を別に取り出して述べている述べているのが分かります。
こうしてみると、大前提「魚は卵を産む」は、広く全体的なコトを述べているので、「一般的」な命題と言えます。
これに対して、結論の「鮭は卵を産む」は、その中で一部を別にして述べているので、「個別的」な命題ということが分かります。
続いて、「普遍的」と「特殊的」という対の語について考えてみます。
「普遍的」とは、すべてのモノに共通しているさまです。すべてのモノに当てはまるということです。
「特殊的」とは、限られた若干のモノにだけ当てはまるさまです。すべてのモノに当てはまっていないわけです。
大前提の「魚は卵を産む」では、「魚」には「鮭」も含む色々な魚があり、「魚」というすべてに共通して当てはまるコトを述べているのが分かります。
これに対して、結論の「鮭は卵を産む」では、「魚」の中でも「鮭」という種類の魚についてのみ述べています。
つまり、「鮭」という「魚」の中の限られたモノを取り出して述べている述べているのが分かります。
こうしてみると、大前提「魚は卵を産む」は、すべてのモノに共通してそうであるコトを述べているので、「普遍的」な命題と言えます。
これに対して、結論の「鮭は卵を産む」は、その中で限られたモノを別に取り出して述べているので、「特殊的」な命題ということが分かります。
たとえば、いつでもどこでも起きる現象を「普遍的な現象」と言ったりします。
これに対して、普通では起こり得ない現象や、ある特定の場所や時間といった限らた状況でのみ起きるような現象を「特殊な現象」と言ったりします。
最後に、「抽象的」と「具体的」という対の語について考えてみます。
「抽象的」とは、多数の物事に共通している性質です。いわゆる一般的で概念的なことと簡単に説明されたりすることが多いです。
「具体的」とは、一つ一つの物事が持つ性質です。こちらは、共通している性質ではなく、一つ一つの物事自体に注目しています。
大前提の「魚は卵を産む」では、「魚」には「鮭」も含む色々な魚があり、「魚」という多数に共通している性質を述べているのが分かります。
これに対して、結論の「鮭は卵を産む」では、「魚」の中でも「鮭」という種類の魚についてのみ述べています。
つまり、「鮭」という「魚」の中の1つの種類が持つ性質について述べているのが分かります。
こうしてみると、大前提「魚は卵を産む」は、多数に共通している性質を述べているので、「抽象的」な命題と言えます。
これに対して、結論の「鮭は卵を産む」は、その中で1つの種類が持つ性質を述べているので、「具体的」な命題ということが分かります。
なお、「抽象化する」と「具体化する」といった動詞で用いられたりすることも多いです。
「抽象化する」の意味は、多数の物事に共通している性質を抜き出すといった理解をすればいいです。
「魚」とは、「マグロ」「鮭」「鯖」等といった個別の具体的なモノに共通している性質を抜き出した、つまり抽象化した概念・言葉です。
たとえば、エラがある、ヒレがある、水中を泳ぐといった性質は、すべての「魚」に共通しています。「マグロ」「鮭」「鯖」と別々に考えるのではなく、共通する性質から、大きく一纏めにして「魚」とくくっているわけです。
もっといえば、「マグロ」も1匹1匹は違う個体なのに、それらに共通する性質を抜き出して「マグロ」としているわけです。
この「抽象化」の「抽」は、抜き出すという意味で、「象」は物の形といった意味ですが、確かに共通している性質たる「形」を「抜き出し」て考えていることが分かります。
「抜き出す」を別の見方をすると、抜き出されなかった性質たる「形」は、考えないで無視すること、つまり「捨てられている」ことになります。
このように、物事から共通する性質を抽象化するときに、それ以外の性質を度外視することを「捨象」といいます。
「抽象化する」と必ず「捨象する」ことになります。コインの裏表の関係です。
図示して見ましょう。
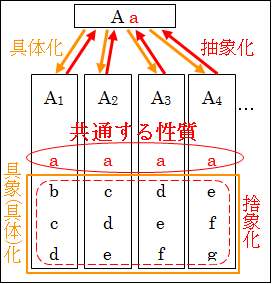
抽象化された概念「魚」をA として、個別の具体的な「マグロ」「鮭」「鯖」といったものをA1、A2、A3 に記号化します。もちろんそれ以外にも、A4、…と個別の具体的なものがあります。
さらに、A1らが持つ性質を、a、b、c、d、…とします。
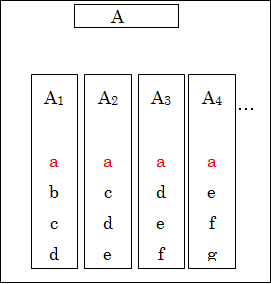
こうして見たとき、A1らに全てに共通する性質は、a だと分かります。
この共通する性質a を抜き出す、つまり「抽象化する」と、Aとなり、性質a を持っているということになります。
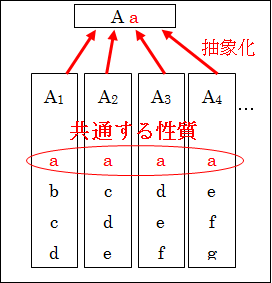
さらに、抽象化されたAを考えているとき、共通する性質a 以外のA1らが持っていた性質b、c、d、…は無視されることになります。つまり「捨象化」されています。
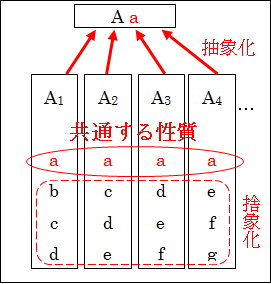
そして、「抽象的」の対義語が「具体的」であったように、「抽象化する」の対義語は「具体化する」です。
したがって、「具体化する」の意味は、抽象化された性質を1つの別個の物事にすることと理解しておけばいいです。
たとえば、実際に漁をするときに、「魚」という大きなくくりで考えても役に立ちません。「マグロ」と「鮭」では獲れる場所や時期が異なります。「魚」ではなく、別個の1つの種として「マグロ」や「鮭」を具体的に考えないといけません。
「具体化」の「具」は、具(そな)えるという意味で、「体」は実体の意味ですので、「実体」を「具えている」ようにして考えていることが分かります。
なお「体」も「象」も「形」といった似た意味がありますが、「体」の方が現実感があり、「象」の方が想像的な感じだと思ってください。
だから、「具体化」の場合は、より現実に近づけていた「形」にすることなので、具「体」化となっており、「抽象化」の場合は、共通した性質の「形」を抜き出しているので、抽「象」化となっています。
したがって、「具体」と同じ意味で「具象」という言葉もあります。「象」の字から分かる通り、意味は微妙に違い、「具象」を別個の性質を具えておりハッキリとそれと分かるといったことになりますが、「具体」と「具象」は同じ意味として捉えておけばいいです。
「具体化」も図示してみます。「抽象化」の図を見てください。この矢印が逆になります。
抽象的な概念A を具体化することで、1つ1つ別個のモノA1、A2、A3、…が導かれます。
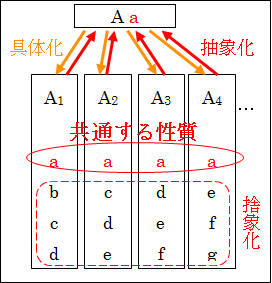
そして、抽象的なA では、共通する性質a のみがありましたが、具体化された1つ1つの別個のモノにはそれぞれが持つ性質b、c、d、…があります。
この具体的な概念A1らが持つ性質は「具象化された」ものです。もちろん「具体化された」といってもいいです。
図4.1.抽象化と具体化
なお、一般的・普遍的・抽象的な概念Aと個別的・特殊的・具体的な概念A1、A2、A3、…を比較したときに、
より抽象度の高い概念Aを上位概念や高次の概念、
より抽象度の低い、つまり具体的な概念A1、A2、A3、…を 下位概念や低次の概念、
と言ったりすることもあります。
3 演繹法の構造
「抽象」と「具体」の話が長くなりましたが、演繹法に戻って考えます。
演繹法の定義が、一般的・普遍的・抽象的な命題や法則を前提として、その前提からより個別的・特殊的・具体的な結論を導く推論方法でした。
これは、先程描いた図4.1で考えると、赤の矢印ではなく黄色の矢印に論理が流れていることを表しています。
つまり、演繹は、一般的・普遍的・抽象的な命題や法則である前提から、より個別的・特殊的・具体的な結論を導いています。
図4.2.演繹法 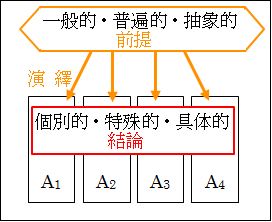
これが演繹法の基本的な形式なのですが、実際に使うときには、三段論法のように考えて使うことが多いです。
では、(4.2)を見てください。
| (4.2)三角形で2つの角が35°と45°のとき、残りの1つの角は何度か。ただし、値だけでなく、どのように答えを導いたかも明確せよ。 <大前提> 魚は卵を産む <小前提> 鮭は魚である [結論] よって、鮭は卵を産む |
今、ある「三角形の2つの角がそれぞれ35°と45°である」ことが分かっています。おそらく、「残りの1つの角は100°である」と答えを導いた人が多いと思います。もちろん結論の「残りの1つの角は100°である」自体は正しいです。
でも、ある「三角形の2つの角がそれぞれ35°と45°である」ことからは直接推論することはできないです。詳しく見て行きましょう。
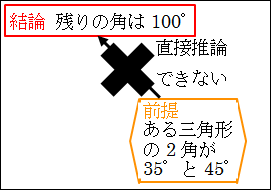
まず、問題文からは、「三角形の2つの角が35°と45°である」ということが分かっていますが、これが推論するための前提になります。
| (4.2)三角形で2つの角が35°と45°のとき、残りの1つの角は何度か。ただし、値だけでなく、どのように答えを導いたかも明確せよ。 < 前提> 三角形の2つの角が35°と45°である [結論] よって、残りの1つの角は100°である |
なぜ前提「三角形の2つの角が35°と45°である」ことから、結論「残りの1つの角は100°である」ことを推論できたのでしょうか。それは、「三角形の3つの角の和は180°である」という知識を暗黙の内に使っているからです。
だとすると、「三角形の3つの角の和は180°である」という定理も、結論を導くための推論に使用しているので、前提の1つと言えます。しかも、問題文にも書かれていないし、数学の試験以外の日常では明示されることも少ないですから、隠れた前提と言えます。
| (4.2)三角形で2つの角が35°と45°のとき、残りの1つの角は何度か。ただし、値だけでなく、どのように答えを導いたかも明確せよ。 < 前提> 三角形の3つの角の和は180°である <隠れた前提> < 前提> 三角形の2つの角が35°と45°である [結論] よって、残りの1つの角は100°である |
そして、2つの前提のうち、どちらがより一般性が高いかと言えば、「三角形の3つの角の和は180°である」の方と言えます。これは、すべての三角形の内角の和について述べているからです。対して、「三角形の2つの角が35°と45°である」は、「すべての三角形」の中の「2つの角が35°と45°の三角形」について述べているので、そうでない三角形を除外していることになりますし、より個別的と言えます。
したがって、「三角形の3つの角の和は180°である」が大前提、「三角形の2つの角が35°と45°である」が小前提、と分かります。
| (4.2)三角形で2つの角が35°と45°のとき、残りの1つの角は何度か。ただし、値だけでなく、どのように答えを導いたかも明確せよ。 <大前提> 三角形の3つの角の和は180°である <隠れた前提> <小前提> 三角形の2つの角が35°と45°である [結論] よって、残りの1つの角は100°である |
何気ないことですが、立派な演繹法による推論をしているのが分かります。
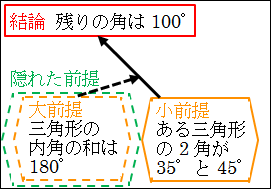
このように演繹法は、
ある事象を発見・観察する。
それに一般的・普遍的・抽象的な命題や法則を適用する。
これによって、個別的・特殊的・具体的な結論が導かれる。
という構造になっています。
図4.3.演繹法の論理構造
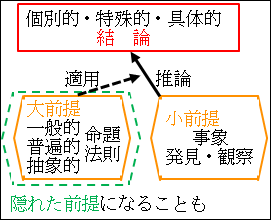
一般的・普遍的・抽象的な命題や法則を大前提とし、
ある事象を小前提とすると、
三段論法の形式になるわけです。
なので、適用する一般的・普遍的・抽象的な命題や法則たる前提は、明示されず隠れた前提になることがあります。
今回の三角形の角度も、数学の試験は別としても、人と話しをしているときに、「三角形の内角の和は180°だから」とわざわざ言う人はあまりいないと思います。
あまりにも当たり前過ぎて、つまり、常識的過ぎて、皆が知っているだろうと考えて、明示しないわけです。
この場合は困ることはあまりないのでいいのですが、議論をする際には、相手と自分が定義や前提を同じように共有しているか不明な部分や、相手が知らないかもしれないと考えられる前提については、明示しておかないといけません。
また、演繹法を逆手にとれば、隠れた前提たる相手の価値観や常識等を推測する手掛かりにもなったりします。
例えば、どんな場合でも「国家権力が肥大化すると、市民の自由が脅かされる」と主張する人がいるとします。
「国家権力が肥大化する」ことが事象 E にあたり、小前提です。
「市民の自由が脅かされる」が、結論となっています。
論理としては、小前提から結論が推論されているわけですが、これだけでは論理が飛躍していることに気付きます。
この主張を論理的または説得的にするためには、「国家権力は人民の権利を侵害する」といった大前提が必要になります。
しかし、「国家権力が肥大化すると、市民の自由が脅かされる」という主張では、明示されておらず隠れた前提になっています。
したがって、どんな場合にもこう主張する者は、「国家権力は人民の権利を侵害する」と考えているのではないか、と推測できるわけです。
もちろん、これは明示されていないものを勝手に推測しているので、常に正しいわけではないです。
相手の価値観等を勝手に理解したり読めたつもりになって議論してはいけません。勘違いが起きないように、隠れた前提について尋ねて確認しておくのがよいでしょう。そして、隠れた前提が明らかになれば、より正確に、より建設的な議論にしていくことができるでしょう。
さらに教科書でも何でもいいのですが、読書等をしていて、論理展開についていけないと感じたりしたら、この隠れた前提は何なのかと考えてみると理解を助けてくられるかもしれません。
4 相対的と絶対的
演繹法の論理構造等を見て来たわけですが、大前提と小前提の違いは、どちらが一般・普遍・抽象的で、どちらが個別・特殊・具体的かというコトに求められました。
しかし、一般的・普遍的・抽象的と個別的・特殊的・具体的といった言葉は常に一定ではありません。何が全体的であり、何が部分的なのかは必ずしも一つに定めることができるとは限らないということです。
つまり、ある場合では一般的・普遍的・抽象的だった命題が、別の場合には個別的・特殊的・具体的な命題になったりします。
例えば、「日本人は物静かだ」と「太郎は物静かだ」とを比べてみます。
「日本人は物静かだ」が一般的で、「太郎は物静かだ」は個別的な話になります。
「太郎」は「日本人」の一部ですから、「日本人」について語っているほうが広い全体的な話で、「太郎」について語っている方が狭い部分的な話になるからです。
それでは、「人間は物静かだ」と「日本人は物静かだ」とを比べて考えてみましょう。
「人間は物静かだ」が一般的で、「日本人は物静かだ」は個別的な話となります。
「人間」は「日本人」だけでなく「アメリカ人」や「中国人」等と様々ですから、「人間」の方が「日本人」よりも広く全体的な話をしているのが分かります。
「日本人」は、「太郎」と比較した場合には一般的な話だったのに、「人間」と比較すると個別的な話になっています。
さらに、「人間は物静かだ」と「日本人は物静かだ」と「太郎は物静かだ」の3つを比べて考えてみます。
最も一般的な話は「人間は物静かだ」で、最も個別的な話は「太郎は物静かだ」で、その中間に「日本人は物静かだ」が位置することになります。
| 一般的・普遍的・特殊的 ↑人間 | |日本人 | ↓太郎 個別的・特殊的・具体的 |
このように、全体的であるのか部分的なのかは比較する対象によって変わるということを肝に銘じておいてください。
そして、今見たように、他と比べたり、他との関係によって、物事が成り立ったり、意味が決まることを「相対的」と言います。
「相対的」の対義語は「絶対的」で、他と比べるたり関係を考慮したりせずに、物事が成り立ったり、意味が決まることです。
「相対的」な場合とは、他との関係により成立したり意味が決まるので、他に制限・制約されているとも言えます。
これに対して、「絶対的」な場合は、他とは無関係に成立したり意味が決まるので、無制限・無制約であるとも言えます。
世の中の多くは相対的であり、人間は何かしらと比較しながらでないと物事を判断できないことが多いです。
例えば、成績がそうでね。100点満点のテストで100点とっても、自分の位置付けが分かる場合は少ないです。100人の受験生が100人とも100点ならば、別に凄くも何とも思わないはずです。
しかし、こうも考えられます。100点は100点だ。満点は何であろうと素晴らしいんだ。このように、100点は無条件に凄いと考えることもできます。つまり、他と比べなくても、他との関係も考えなくても、100点それ自体が凄いと考えるというわけです。これは絶対的なモノの見方です。
でも、実際にそう考える人はあまりいないでしょう。もし、80人位が50点以下で、29人が51~99点を取っていて、自分が100点取ったとします。これならば、凄いと思えるわけです。
これは、他の人の成績と比較して、他の人の成績との関係によって、自分の成績がどういった意味合いを持つのかを判断していると言えます。まさに相対的に考えているわけです。
このように、物事が一般的・普遍的・抽象的なモノなのか、個別的・特殊的・具体的なモノなのかは、比べられる対象同士の関係によって決まってくる場合がほとんどだということを忘れないでください。
ある時は抽象的な概念が、別の時には具体的な概念として扱われたりします。そのときは、議論がどのレベルの抽象度で進んでいるのか等をしっかりと把握しておかないと混乱の元になったりします。
5 まとめ
以上、三段論法と演繹法について学びました。
演繹法は、前提が真であり、推論が正しく行われていれば、それによって導かれる結論も必ず真になるため、議論や推測を行うとき強力な武器になります。
それに加えて、論理的思考に必要な「一般的・普遍的・抽象的」と「個別的・特殊的・具体的」といった対の用語と「相対的」と「絶対的」という概念の意味も学習しました。
演繹法は日常の生活でも意識的にしろ無意識的にしろ使っている推論形式ですが、その意味を今一度しっかりと理解しておくことが重要です。何となく形式が整ったような気がする推論は、論理的思考ができているとは言い難いことがよく分かると思います。
演繹法とは、一般的・普遍的・抽象的な命題や法則を前提として、その前提からより個別的・特殊的・具体的な結論を導く推論方法である、
という定義と、論理構造をしっかりと身に付けて、細かい推論の注意点は三段論法の形式でチェックすることを日頃から意識して練習して、無意識にできるようになりましょう。
図4.3.演繹法の論理構造 
次は、演繹法とは逆の推論方法である帰納法について学びましょう。
前頁:第3章 三段論法
ページトップへ:第4章 演繹法
次頁:第5章 帰納法