前頁 |▼| 次頁
第7章 類比推論
仮説推論と同様に、帰納法の中で、必ずしも正しい推論とは言えないが、重要な推論方法が類比推論です。
類比推論は、物事の似た部分に注目してそこから何かしらを推論する方法です。
これは人間誰しもが持つ考え方で、日常でも多く使用しているので、身近なものかと思います。
| 目次 |
| 1 定義と特徴 2 狭義の帰納法との比較 3 科学と比喩 テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 定義と特徴
推論する際には、形式として演繹法をとるにしろ帰納法をとるにしろ、様々な事柄に共通項を見出して論理的思考を用いて来たのが理解できたはずです。特に狭義の帰納法は、様々な個別・特殊・具体的な事柄から共通項を抜き出し抽象化して、一般・普遍・抽象的な命題や法則を推論するものでした。狭義の帰納法は、必要で十分の事例を前提にする必要がありましたが、日常では圧倒的に少ない事例から、共通項を見つけ出して、推論していることが多いです。
しかし、現実問題として、必要で十分な事例をいつでも集められるとは限りません。また、仮説推論がそうであったように、何かを考える最初の取っ掛かりとして、ちょっとくらいの論理の飛躍は許されるべきと言ってもよいのではないか。最初は論理的思考と言えないコトから始まっても、論理的に主張が組み立てられたらよいのではないか、という考え方があることも学びました。そこで、仮説推論と同様に、論理的思考と言うには、少し思い付き的なコトから出発する推論をもう1つ学びましょう。
それが、類比推論と呼ばれる推論方法です。これは、ある特定の物事の特徴から、他の特定の物事の特徴を推論する方法です。
英語では、analogy と言います。類比推論は類似推論とも言われることもありますし、「類」比「推」論を短縮して類推と言ったりもします。種類という言葉からも分かる通り、「類」は「互いに似ている」という意味です。「比」には「くらべる」といった意味がありますから、「類比」とは「互いに似たものを比べる」というコトになります。また、「類似」も「類」と「似」も同じ意味の漢字を重ねた言葉であり、「互い似ていること」ということです。したがって、類比推論と類似推論は、似たものを比べる推論ということが文字からも分かります。ここでは、「比べる」という意味をより意識したいので、言葉としては類比推論を使うようにします。
さて、類比推論が、ある特定の物事の特徴から、他の特定の物事の特徴を推論する方法ですが、この思考方法も、アリストテレスの時代から整理され、それ以後も色々と研究されてきました。こうした中で、イギリス経験論のフランシス・ベーコンや、ジョン・スチュアート・ミルが、類比推論は帰納法の特殊なものである、と整理しました。
では実際に、ある特定の物事の特徴から、他の特定の物事の特徴を推論するとはどういうことか見てみましょう。(7.1)を見てください。
| (7.1)類比推論の例 <前提1> シイタケとカキシメジは色や形が似ている <前提2> シイタケは食べられる [結論] よって、カキシメジも食べられるはずだ |
この推論は演繹法ではありません。枚挙的帰納法つまり狭義の帰納法と呼べる程に大量の事実を観察しているわけでもありません。
「シイタケは食べられる」という事実を前提にして、「シイタケとカキシメジは色や形が似ている」ということを理由に挙げて、「カキシメジも食べられるはずだ」と結論付けています。「カキシメジが食べられるはずだ」という結論の根拠は、「シイタケが食べられる」ことと「カキシメジが、食べられるシイタケと色や形が似ている」こととなっています。
つまり、「似ている」ということが推論の根拠の中心になっています。これが類比推論です。
この類比推論を記号化して形式化してみます。
| 類比推論 <前提1 > α とβには共に、a、b、c、…という特徴があり、類似である <前提2> αには、(a、b、c、…と関連する) x という特徴がある [結論] よって、βにも、(a、b、c、…と関連する) x という特徴がある |
αとβは、2つの概念です。
a、b、c、…は、αとβが持つ特徴です。つまり、αとβに共通する要素が a、b、c、…であるということです。普通は共通要素は複数あることが多いですが、1つしかないときもあります。
αとβの特徴として、共通する要素が、a、b、c、…とあるので、類似していると言えるわけです。
図7.1.類比推論の構造
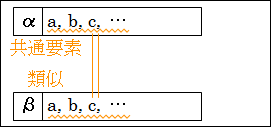
そして、αには特徴として、共通する要素が、a、b、c、…に関連する要素 x があることに気付きます。ここで、「共通する要素が、a、b、c、…に関連する」と付けている理由は、類似性から推論するので、要素 x も、共通する要素が、a、b、c、…に関連しているものになります。ただし、必ずしも関連性がハッキリと分からないこともあります。
図7.1.類比推論の構造
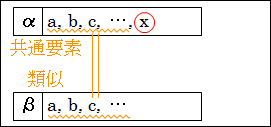
したがって、αとβの特徴として、共通する要素が、a、b、c、…とあり類似しているのだから、βにも特徴として、要素 x があるはずだと推論しています。
図7.1.類比推論の構造
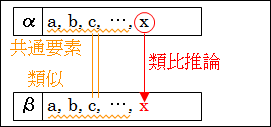
つまり、簡単に言えば、αとβはこんなに似ているのだから、多分だが、要素 x もβにあるはずだと考えているわけです。
記号化したものを(7.1)に照らして言うと、
「α」は「シイタケ」で、「β」は「カキシメジ」ということになります。
共通要素 a、b、c、…は、「キノコ」、「傘の色が褐色」、「傘と柄の形が似ている」、…といったものになり、類似していると考えられます。
共通する要素 a、b、c、…に関連する要素 x は、「食べられる」ことになります。「食べられる」ことは、「キノコ」「傘の色が褐色」、「傘と柄の形が似ている」、…という共通要素と関連していると言えます。
「カキシメジ」が「食べられる」かどうかは分かりません。しかし、「シイタケ」と似ているのだから、「シイタケ」が「食べられる」ので、「カキシメジ」も「食べられる」という特徴を持っていると考えられる、と推論しています。
なお、αとβは類似していることは、殊更に明言されずに、隠れた前提になることもあります。(7.1)で言うと、「シイタケは食べられる」から「カキシメジも食べられるはずだ」と述べられることもあります。
または、推論される特徴たる要素 x が明言されずに、隠れた前提になることもあります。(7.1)で言うと、「シイタケとカキシメジは色や形が似ている」から「カキシメジも食べられるはずだ」ということになります。
これは隠れた前提にしても、類似性があるのだから、わざわざ前提をすべて述べなくても、聞き手が隠れた前提を補って理解してくれると話し手が考えているからと言えます。したがって、一見して類似性が分からなかったり、その類似性があまり一般的な知識ではないならば、隠れた前提にせずしっかりと述べるほうがいいです。
このように、類比推論は、物事に共通する特徴に注目し類似性を見つけ出して、その類似性を理由に、ある物事が持つ特徴をもう一つの物事が持つことを推論する方法です。
ちなみに、カキシメジは、シイタケに似ていますが、毒キノコで食べられないので注意してください。もし食べると、頭痛、腹痛、下痢、吐き気等に苦しむことになります。
このように、類比推論は物事の類似性に注目して推論しているだけなので、必ずしも推論の結果である結論が正しいとは限りません。そもそも、類比推論は、帰納法の特殊な形態と言えるので、結論が必ずしも正しくならないことは納得できます。
ページトップへ
2 狭義の帰納法との比較
ここで帰納法の特殊な形態と言った理由は、観察する事例が極端に少ないのに、それが持つ特徴の類似性を前提として推論しているからです。類比推論と狭義の帰納法との共通点と相違点を改めて確認しみましょう。
共通点として、類比推論も狭義の帰納法も、観察された事実から、観察されていない事実を推論します。
類比推論では、「シイタケが食べられる」ことと「シイタケとカキシメジが似ている」こと以外は観察されていないのに、「カキシメジが食べられる」という観察されていない結論を推論しています。
狭義の帰納法では、「あるシイタケA1は食べられる」、「あるシイタケA2は食べられる」、…と観察を続けて、「すべてのシイタケは食べられる」という観察されていない結論を推論しています。
このように、類比推論も狭義の帰納法も、観察された事実から、観察されていない事実を推論する点で同じと言えます。
相違点として、類比推論は1つのコトから多くのコトを推論するのに対して、狭義の帰納法は多くのコトから1つのコトを推論します。
類比推論では、「シイタケが食べられる」という1つの事実から「カキシメジが食べられる」と推論しています。本来、「シイタケ」と「カキシメジ」は「キノコ」で似ているとは言え、全く別の物です。にもかかわらず、「カキシメジが食べられる」という結論を推論しています。1つの物である「シメジ」から、もう1つの物である「カキシメジ」を推論しており、一から多となっています。
狭義の帰納法では、「あるシイタケA1は食べられる」、「あるシイタケA2は食べられる」、…と観察を続けて、「すべてのシイタケは食べられる」と推論しています。これは多くの観察事実から、1つの結論「すべてのシイタケが食べられる」と推論していることになります。あくまで多くの「シメジ」から1つの「シメジ」の特徴のみを推論しています。つまり、多から一となっています。
このように、類比推論と狭義の帰納法は、一から多へ、多から一へという点で異なると言えます。
3 科学と比喩
類比推論では、結論が必ずしも正しくならないとは言え、何かしらを考える際に、最初の取り掛かりとしては、強力な思考法であることを先程説明しました。この思考の最初の一歩という意味では仮説推論と似ています。仮説推論と似ているということは、類比推論の結論も一種の仮説と考えられます。したがって、仮説検証が重要になり、結論が正しいかどうかを実際に調べる必要があります。
類比推論は仮説なのか?、と思った人は、先程の「シイタケ」と「カキシメジ」の例を思い出してください。もし類比推論が、演繹法とまでは言えなくても狭義の帰納法と同じ位の確からしさで結論を導けるとしたら、何故「カキシメジ」は実際に食べられなかったのに「食べられる」と結論づけられたのでしょうか。これは、仮説であり、論理的思考よりも思い付き的な面が強いからです。
1 類比推論と科学
その他にも、類比推論が、思考法の最初の一歩ということは、枚挙に暇がありません。
例えば、物理学における力学の考え方は、電磁気学に類比推論を適用することで発展しました。有名なのが19世紀のイギリスの物理学者であるファラデーとそれをさらに発展させたマックスウェルです。
力学の分野と電磁気学の分野で起きている現象を比べて、何かしら似ていることに気付き、実際に力学の考え方で電磁気学の説明を試みようしたわけです。もちろん、類比推論をしただけでは、実際に結論が正しいとは限らないわけですから、検証する必要があります。そこで実験を重ねて、類比推論で得られた結論通りになっていることを確認していきます。また、数式を用いて方程式で現象を表して正しさを証明していきます。そうすると、今まで力学と電磁気学は別の分野であったはずなのに、統一的な法則で説明できるようになったわけです。この偉大な成果の最初の第一歩は、類比推論でした。これについてもっと詳しく知りたい人は、物理学の勉強をしてください。
現代も、科学の分野では色々と類比推論から着想、つまり、最初の発想を得て、得て色々と研究をしています。
仮説推論でも述べましたが、私達人間は事実を観察するだけでは、中々新しいコトは思いつきません。必ずしも論理的思考とは言えないような方法、つまり、自分の持っている経験や知識等と結びつけることで、何かを思いついたり、主張の結論を得ます。思い付きはよく私達を誤らせますので、それが本当に正しいかどうか確かめていくわけです。そして、時には全く関係ないと思われていた分野の知識を類比推論することで新しい知識が生まれることも少なくありません。
2 類比推論と比喩
また科学の知識以外にも、日常生活で誰かに何かを説明するとき分かりやすくするため、類比推論を用いることがあります。
いわゆる比喩というやつです。英語では、trope と言います。比喩は、ある物事を、類似または関係する他の物事を借りて表現することです。
論理的思考では、難しい事柄または馴染みの薄い事柄を、分かりやすくするために、易しい事柄または馴染みの深い事柄に喩えることで使うことが多いです。
単純化すると「α は、β である」という形で表されます。
α が、喩えられるコトで、難しい事柄または馴染みの薄い事柄です。
β が、喩えるモノで、易しい事柄または馴染みの深い事柄です。
| 比喩の一般的形式 α は、β である α:喩えられること 難しい事柄または馴染みの薄い事柄 β:喩えるもの 易しい事柄または馴染みの深い事柄 |
分かり難いα を、β で喩えることで、理解しやすくします。そして、β で喩えられるとα が理解しやすくなる理由は、α とβ の類似性があるからです。
そもそも、α がよく分からないというのは、α が持つ特徴 a、b、c、…が掴めないため、具体的なことが分からないからです。それならば、α を理解するためには、α が持つ特徴 a、b、c、…が理解できればいいと分かります。
図7.2.比喩の構造
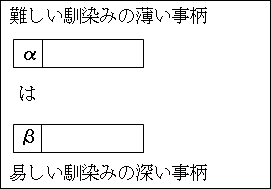
そこで、より易しく馴染みの深いβ が、αが持つ特徴 a、b、c、…と持っているために似ていることを利用します。
図7.2.比喩の構造
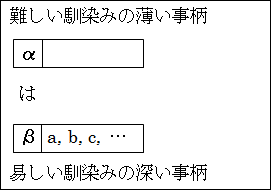
そして、β は、易しく馴染み深いので、理解ができています。したがって、β が持つ特徴 a、b、c、…も理解できていることになります。
図7.2.比喩の構造
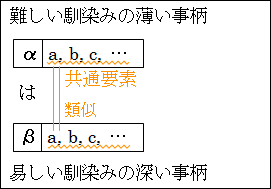
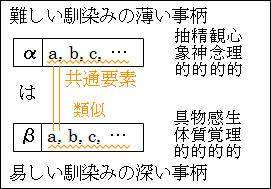
そうすると、共通要素があり似ているため、β を通じて、α の特徴 a、b、c、…を把握することができます。
これが比喩の構造となっています。逆に言えば、比喩が分からないときには、α とβ の類似性に注目することで比喩が理解できます。
比喩は、直喩と暗喩があります。直喩は明喩、隠喩は暗喩と言われることもあります。英語では、直喩は simile で、隠喩は metaphor と言います。隠喩の方は日本語でもメタファーと言われることが多いですが、直喩は何故かシミリーと表されることが少ないです。
直喩は、「α は、まるで β のようだ」のように、「あたかも」や「まるで」、「ようだ」や「如し」といった表現で比喩だというコトが直接分かるように喩えることです。
例えば、(7.3)の「雨が、滝のように降る」を考えてみます。
| (7.3)直喩 雨が、滝のように降る |
これは、「ように」があり直喩だと分かります。「雨が降る」という様を、「滝のように」と喩えているわけです。
| (7.3)直喩 雨が、滝のように降る →雨が降る様は、滝のようだ |
「雨が降る様は、滝のようだ」とは、「雨がものすごい大量に降る」ことを示しているのは分かると思います。
| (7.3)直喩 雨が、滝のように降る →雨が降る様は、滝のようだ =雨がものすごい大量に降る |
ただ「ものすごい大量に」と言っても、曖昧ですし、想像し難いところがあります。
そこで、「滝のように」と喩えることで、「雨がものすごい大量に降る」ことが想像しやすくなります。その理由として、「滝」が持つ特徴に、「水量が凄い」ということがあります。この特徴は多くの人が抱くものかと思います。
| (7.3)直喩 雨が、滝のように降る →雨が降る様は、滝のようだ 水量が凄い =雨がものすごい大量に降る |
つまり、「雨がものすごい大量に降る」ことと「雨が滝のように降る」こととの類似点は、「水量が凄い」ことと言えます。
また、「水量の凄さ」以外にも、
「雨」の特徴が、「水」であり、「上から下へ落ちる」こと
と
「滝」の特徴が、「水」であり、「上から下へ落ちる」こと
と共通しています。
| (7.3.1)直喩 雨:水、上から下へ 滝:水、上から下へ、水量が凄い |
したがって、「雨が、滝のように降る」と言ったとき、「水量が凄い」ことが自然と想像しやすいと言えます。
| (7.3.1)直喩 雨:水、上から下へ、水量が凄い 滝:水、上から下へ、水量が凄い |
もし「雨がアマゾン川のように降る」と言ったら、多くの人は、ん?、となるはずです。
「アマゾン川」も大きな川だけあって、確かに水量は凄いです。しかし、「雨」や「滝」ほどに上から下へ落ちるということを経験から呼び起こされません。だから、「雨が滝のように降る」と言えば、分かりやすい比喩になりますが、「雨がアマゾン川のように降る」と言うと奇妙に感じるのです。
このように、比喩は適切に使わないと、かえって混乱を引き起こすので、喩えられるモノα と喩えるコトβ の類似性や共通性を上手く踏まえて使わないといけません。
直喩が比喩だと直接分かるような比喩であるならば、比喩だと直接は明示されない比喩もあります。それが隠喩です。
隠喩は、「α は、β だ」という形式で表されます。直喩と違う点は、「あたかも」や「まるで」、「ようだ」や「如し」といった表現で直接比喩と分かるような表現がないことです。
例えば、(7.4)の「王の怒りは、燃え盛る炎だった」を考えてみます。
| (7.4)隠喩 王の怒りは、燃え盛る炎だった |
「王の怒り」が「燃え盛る炎」であるはずがありません。「怒り」とは物質ではなく気持ちなので、火がついて燃えるというのは現実に起こり得ません。しかし、「王の怒りは、燃え盛る炎だった」という表現を私達は受け入れられます。何故でしょうか。
これは、「怒り」を「炎」で喩えているからだと言えます。そして、「まるで」や「ようだ」といった直接比喩表現だと分かる言葉がないので、隠喩になります。したがって、「王の怒り」の様を、「燃え盛る炎」と言っているわけです。「王の怒りがものすごい」ことが、「燃え盛る炎」で喩えられていることが分かります。
| (7.4)隠喩 王の怒りは、燃え盛る炎だった =王の怒りはものすごい |
ただ「ものすごい」と言っても、曖昧ですし、想像し難いところがあります。
そこで、「燃え盛る炎」と喩えることで、「王の怒りがものすごい」ことが想像しやすくなります。その理由は、「燃え盛る炎」が持つ特徴にあります。「燃え盛る炎」というと、メラメラと勢いよく燃えている炎が想像されます。メラメラと勢いよく燃えている炎とは、どのようなものかと言えば、
| (7.4)隠喩 王の怒りは、燃え盛る炎だった 激しい、簡単に消えない 近寄るだけでも危険 =王の怒りはものすごい |
つまり、「王の怒りはものすごい」とは、「燃え盛る炎」との類似点から、「激しく」「簡単に消えず」「近寄るだけでも危険」なほどだと分かります。
直喩と隠喩の他にも、比喩には、擬人法という有名な比喩表現があります。英語では、personification と言います。擬人法は、人間ではないモノやコトを、人間であるかのように表現する方法です。
例えば、「雲の隙間から月がウィンクした」と言えば、擬人法になります。月には目がないので、ウィンクができるはずがありません。これは、通常人間がするコトを月が行っていると喩えていることになります。
「ウィンク」とは「片目を一瞬閉じて目配せをする」ことですから、「雲の隙間から月がウィンクした」は、
「一瞬」、つまり、「雲の隙間」から少しだけ「月」が見えたこと、
「目配せ」、つまり、「月」が自分に何かを伝えていること、
が分かります。このように擬人法は、人間ではないモノやコトを、人間であるかのように喩える方法になります。
また、擬人法の他に有名なものとして、声喩があります。声喩とは、音声や状態を、言葉で喩える比喩方法です。したがって、声喩は、音声に対する比喩として擬音語や擬声語があり、状態に対する比喩として擬態語があります。
擬音語・擬声語の例として、犬の鳴き声を「ワンワン」と表したり、猫の鳴き声を「ニャーニャー」と表すことが挙げられます。
擬態語の例として、雨が激しく降る状態を「ザーザー」と表したり、炎が激しく燃える様を「メラメラ」と表すことが挙げられます。
英語と比較すると、日本語で声喩表現が豊かと言えますし、実際、生き生きと場面を描写する場合等には色々と便利です。
ただし、論理的思考では、比喩表現はあまり使わない方がいいです。
比喩表現を使わずに、できるだけ具体的で直接的な表現で述べるのが基本です。比喩表現を使う場合には、主張を理解しやすくするための補助としてのみ使うに留めた方がよいです。小説等のような文学であれば、主張を直接表現せずに比喩を用いることで、多様な意味を持たせ、美への意識を喚起することが重要になってきますが、論理的思考は違います。
もちろん、「犬の鳴き声」を「犬の鳴き声」と言わずに「ワンワン」と言っても問題ないことも多いです。しかし、比喩は、類似点を見つけ出すことを相手に委ねてしまうことになります。とすると、解釈に幅が生じやすいです。つまり、人によって、受け取る意味が変わりやすいということです。
解釈に幅が生じるのは、論理的思考ではマズいです。論理的に物事を考えて、前提を積み重ねていくと、1つ結論にたどり着くことを目指しているのに、意味が無くなってしまうからです。したがって、比喩を使う場合には、理解の補助として使うのであって、それとは別に具体的で直接的な表現が中心になることを肝に銘じておいてください。
補足として、比喩では類似点に注目すると言ってきましたが、類似性ではなく隣接性や包含関係に注目する場合もあります。
代表的なのが、換喩と提喩です。換喩は、英語で metonymy と言い、提喩は、英語で synecdoche と言います。
隣接性とは、α とβ の間に密接な関係性があることを意味します。この隣接性に注目する比喩が、換喩です。
包含関係とは、α とβ の間に上位概念と下位概念の関係性があることを意味します。この包含関係に注目するのが、提喩です。
換喩とは、喩えられるコトα と喩えるモノβ の隣接性に注目した比喩です。つまり、α とβ には、非常に密接な関係性があるため、喩えられるα を喩えるβ で表すことで、喩えられるα だと分かる構造になっています。
具体例として、古文でよく出て来る「北の方」とは、「正妻」のことを意味しますが、これは、「正妻」が家の北側にある部屋に住んで居ていたことに由来します。つまり、「正妻」と「北の方」に密接な関係性、つまり、隣接性があることが分かります。だから「北の方」と本来場所を表す語が、「正妻」という人を表すことと理解することができます。
同様の例は、「ホワイトハウスの考え」にも見て取れます。本来は、「ホワイトハウス」と言うと建物のことを言いますが、「ホワイトハウス」に「アメリカ大統領」が住んでいることから転じて、「アメリカ大統領」を指すことがあります。したがって、「ホワイトハウスの考え」と言うと、「アメリカ大統領の考え」という比喩表現になっています。
提喩とは、喩えられるコトα と喩えるモノβ の包含関係に注目した比喩です。つまり、α とβ の間には上位概念と下位概念の関係性があるため、喩えられるα と喩えるβ で表すことで、喩えられるαだと分かるという構造になっています。
具体例として、有名な諺で「人はパンのみに生くる者にあらず」があります。ここで「パン」は、そのものズバリ「パン」ではありません。「パン」の上位概念「食べ物」を指しています。または、「食べ物」のさらに上位の概念である「物質的な充足」を指しているとも考えれます。つまり、「パン」は大きく見れば「食べ物」に含まれており、「パン」が下位概念、「食べ物」が上位概念という関係になっています。この諺の意味は、「人間は物質的な満足のみを目的に生きているわけではない」ということです。この諺を正しいとすると、最低限の衣食住がそろっているだけでは「人間」として生きるには足りないんですね。
他にも、男女の話で「食事に行く」と言うと、「デートをする」ことを意味したりする場合もあります。「デート」には「遊びに出かける」、「喫茶店で休憩する」、「食事をとる」と様々なコトを含みます。つまり、「デート」は上位概念で、「食事」は下位概念となります。このように、「デートをする」と敢えて言わずに、「食事に行く」とぼかすわけです。その理由は、浮気ではないと彼女に言い逃れをするためですが。
換喩や提喩も、広く見れば類似性に注目していると考えられますが、隣接性や包含関係で考えた方が分かりやすいかと思います。
4 まとめ
類比推論は、ある特定の物事の特徴から、他の特定の物事の特徴を推論する方法でした。
そして、類比推論は、仮説推論と同様に、検証を必要としますが、何かを考えるための最初の一歩として、非常に役立つ思考方法でした。
| 類比推論 <前提1> α とβ には共に、a、b、c、…という特徴があり、類似である <前提2> αには、(a、b、c、…と関連する) x という特徴がある [結論] よって、βにも、(a、b、c、…と関連する) x という特徴がある |
αとβの特徴として、共通する要素が、a、b、c、…とあり類似しているのだから、βにも特徴として、要素 x があるはずだと推論しています。
図7.1.類比推論の構造

そして、類比推論は、比喩表現にも応用できました。類似性に注目して、理解を助ける効果があります。
| 比喩の一般的形式 α は、β である α:喩えられること 難しい事柄または馴染みの薄い事柄 β:喩えるもの 易しい事柄または馴染みの深い事柄 |
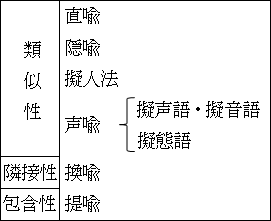
比喩には類似性に注目する直喩と隠喩、擬人法、声喩がありました。
声喩には、擬声語・擬音語と擬態語に分けられました。
また、比喩には隣接性に注目する換喩がありました。
そして、包含関係に注目する提喩がありました。
前頁:第6章 仮説推論
ページトップへ:第7章 類比推論
次頁:第8章 観念連合