前頁 |▼| 次頁
第5章 帰納法
演繹法が一般的・普遍的・抽象的な前提から、個別的・特殊的・具体的な結論を推論するものでした。
その逆の流れを学びます。
つまり、個別的・特殊的・具体的な前提から一般的・普遍的・抽象的な結論を推論する方法で、帰納法と言います。
さらに、帰納法と演繹法の違いも比較しながら理解していきます。
| 目次 |
| 1 定義 2 帰納法の問題点 3 演繹法との絡み 4 演繹と帰納の比較 5 応用 テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 定義
復習ですが、演繹法は、一般的・普遍的・抽象的な命題や法則を前提として、その前提からより個別的・特殊的・具体的な結論を導く推論方法である、と定義されました。帰納法は、この逆の推論となります。この逆というのは、前提と結論を入れ換えるということです。
つまり、
帰納法とは、個別的・特殊的・具体的な命題を前提として、その前提からより一般的・普遍的・抽象的な結論を導く推論方法である、
と定義できます。ちなみに英語では、induction と言います。また、inductive reasoning と言うこともあり、日本語では帰納法的推論や帰納的推論になります。呼び方は様々にありますが、ここでは演繹法と呼称をそろえるためにも、帰納法と呼ことを基本とします。
この帰納法という思考方法を体系化した人で有名なのが、フランシスコ・ベーコンです。ベーコンは16世紀後半から17世紀の初めにかけて活躍したイギリスの哲学者です。ベーコンは、実験や観察を重視ししており、帰納法のように経験に基づく推論方法を提唱しました。こうしたベーコンの思想の流れをイギリス経験論と呼びます。
では、実際に個別的・特殊的・具体的な命題を前提として、一般的・普遍的・抽象的な結論を推論する過程を見てみましょう。(5.1.1)を見てください。
| (5.1.1)次の前提から得られる結論は何か。 <前提1> マグロは泳ぐ <前提2> 鮭は泳ぐ <前提3> 鯖は泳ぐ [結論] よって、 |
前提1「マグロは泳ぐ」、前提2「鮭は泳ぐ」、前提3「鯖は泳ぐ」、…と複数の前提から何が導けるでしょうか。
こうした個別的・特殊的・具体的な命題の集まりから、一般的・普遍的・抽象的な命題を導くのが帰納法なわけですから、何かしら共通する事柄を抜き出せないか考えてみます。
主語は「マグロ」「鮭」「鯖」とすべてバラバラですが、述語は「泳ぐ」とすべてに共通しています。ということは、「~は泳ぐ」という形になりそうだと予想できます。
| (5.1.1)次の前提から得られる結論は何か。 <前提1> マグロは泳ぐ <前提2> 鮭は泳ぐ <前提3> 鯖は泳ぐ [結論] よって、 は泳ぐ |
では、バラバラの主語である「マグロ」「鮭」「鯖」に共通していることはなんでしょうか。
「マグロ」「鮭」「鯖」らは、すべて「魚」に分類されます。したがって、「マグロ」「鮭」「鯖」を抽象化して「魚」という概念を引き出すことができます。
| (5.1.1)次の前提から得られる結論は何か。 <前提1> マグロは泳ぐ <前提2> 鮭は泳ぐ <前提3> 鯖は泳ぐ [結論] よって、魚は泳ぐ |
以上から、結論として「魚は泳ぐ」ということが導けます。
このように、個別的・特殊的・具体的な命題を前提として、その前提からより一般的・普遍的・抽象的な結論を導く推論方法と定義される帰納法で推論する際には、複数の個々の前提における本質的な共通事項や関係を抜き出していることが分かります。
つまり、帰納法で推論するときは、何らかの共通性は無いか、その共通性から一般化・普遍化・抽象化できないかといった思考をしていると言えます。
一応、復習を兼ねて確認ですが、個々別々の事柄における共通事項を抜き出しているということは、抽象化しているということですね。
確かに、前提の「マグロ」「鮭」「鯖」と結論の「魚」を比較すると、前提の方が個別的・特殊的・具体的であるのに対して、結論の方は一般的・普遍的・抽象的と言えます。
記号化してみましょう。
前提の主語を、S1、S2、S3、…と置き、述語をPとします。
それぞれ別個の前提のS1、S2、S3、…から抽象化された結論の主語をSnとします。
そうすると、帰納法による推論は次のように図示できます。
図5.1.帰納法の論理構造1
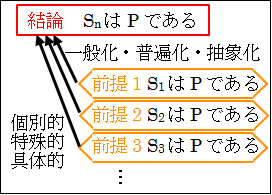
今、前提の主語が異なる場合を見たので、次は、前提の述語が異なる場合を見てみましょう。
| (5.1.2)次の前提から得られる結論は何か。 <前提1> T大学には数学科がある <前提2> T大学には物理学科がある <前提3> T大学には化学学科がある [結論] よって、 |
前提1「T大学には数学科がある」、前提2「T大学には物理学科がある」、前提3「T大学には化学学科がある」、…と複数の前提から何が導けるでしょうか。
帰納法ですから、何かしら共通する事柄を抜き出せないか考えてみます。
主語は「T大学」ですべてに共通していますが、述語は、「数学科がある」、「物理学科がある」、「化学学科がある」とバラバラです。ということは、「T大学には~である」という形になりそうだと予想できます。
| (5.1.2)次の前提から得られる結論は何か。 <前提1> T大学には数学科がある <前提2> T大学には物理学科がある <前提3> T大学には化学学科がある [結論] よって、T大学には |
では、バラバラの述語である「数学科がある」、「物理学科がある」、「化学学科がある」に共通していることはなんでしょうか。
「数学科がある」、「物理学科がある」、「化学学科がある」らに共通するのは、「理数系」の科目であることに気付きます。したがって、「数学科がある」、「物理学科がある」、「化学学科がある」らを抽象化して、「理数系の学科」という概念を引き出すことができます。
| (5.1.2)次の前提から得られる結論は何か。 <前提1> T大学には数学科がある <前提2> T大学には物理学科がある <前提3> T大学には化学学科がある [結論] よって、T大学には理数系の学科がある |
以上から、結論として「T大学には理数系の学科がある」ということが導けます。
記号化してみます。
前提の主語を S とし、述語を、P1、P2、P3、…と置きます。
それぞれ別個の前提の P1、P2、P3、…から抽象化された結論の述語を Pnとします。
そうすると、帰納法による推論は次のように図示できます。
図5.2.帰納法の論理構造2
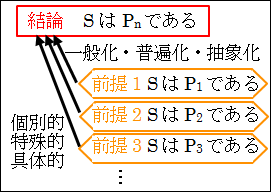
帰納法の論理構造をまとめると次のように、一般化できます。
図5.3.帰納法の論理構造
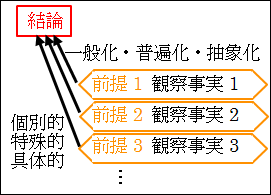
このように帰納法による推論は、
個別的・特殊的・具体的な命題を前提として、その前提からより一般的・普遍的・抽象的な結論を導く推論方法であり、
複数の個々の前提における本質的な共通事項や関係を抽出することが重要だ、
ということが分かりました。
2 帰納法の問題点
帰納法が、複数の個別的・特殊的・具体的な前提から、一般的・普遍的・抽象的な結論を導くのはいいのですが、ここで確認しておきたいことがあります。
そもそも、正しい前提から、正しく推論されれば、結論は必ず正しくなるというのが論理学の利点でした。三段論法に代表される演繹法では確かに成り立っていました。それでは、帰納法でも、前提が真だとして、それから正しく推論されれば、結論が必ず真となり得るのかということです。
どうでしょうか。帰納法の問題点に気付いたでしょうか。(5.1.1)をもう一度見てください。
| (5.1.1)帰納法の特徴1 <前提1> マグロは泳ぐ <前提2> 鮭は泳ぐ <前提3> 鯖は泳ぐ [結論] よって、魚は泳ぐ |
(5.1.1)は、本来ならば、「マグロは泳ぐ、かつ、鮭は泳ぐ、かつ、鯖は泳ぐ、かつ…」と連言の言葉「かつ」で繋げていけば、常に正しい結論になります。
これに対して、帰納法では、「マグロ」「鮭」「鯖」より上位概念である「魚」を用いて、「魚は泳ぐ」と推論しています。ここでの「魚」は、全称「すべての」が省略されているので、実質的に「すべての魚は泳ぐ」ということになります。
仮に、世界のすべての種類の魚を調べて泳ぐことを確認したならば、複数のそれぞれの個別的・特殊的・具体的な前提が真であると言えますし、すべての「魚は泳ぐ」という結論は真と言えます。
しかし、実際問題として、この世のすべての種類の魚を調べることはできるのでしょうか。
すべての種類の魚を調べたと言うためには、もう未発見の種類の魚がいないことも確認しないといけません。未だに新種の生物が発見されている中で、すべての種類の魚を調べたと確信を持つことは困難と言えるでしょう。さらに、すべての種類の魚を調べている過程で、もし泳がない魚を発見してしまったら、前提の1つが偽となってしまいます。
つまり、現実的に前提となるすべての場合を調べることは不可能であるため、帰納法によって導かれる結論は常に正しいと言うことは難しいということが分かります。
すべての場合を調べた確証がない場合に、「すべての魚は泳ぐ」という命題は、真である確率が高いとしか言えないわけです。
1万や10万、それ以上の個別的・特殊的・具体的な場合を調べでも、すべての場合を網羅したとは言い難いですが、ある程度の場合を調べたので、「すべての魚は泳ぐ」と結論づけられ、それが正しい確率が高いということになります。
そして、1つでも偽となる前提が見つかれば、「すべての魚は泳ぐ」とは言えなくなります。全称の「すべて」を使わず、「ほとんどの魚は泳ぐ」とするか、「ある魚を除いて、すべての魚は泳ぐ」と条件を絞って言うしかありません。
このように、ある事態が成立する確率が高いことを蓋然性や確度が高いと言ったりします。確実性が有るか無いか、どの程度のものなか、ということが問題になるわけです。
蓋然性や確度を高めるのは簡単です。調べる前提の数をひたすら増やしていけばいいわけです。観察の対象の数を増やせば増やすほど、その命題の確からしさが増大することを、確証性の原理と言います。
ただ、帰納法にこのような問題点があるといっても、その推論方法の強力さは捨てがたいです。また、実際問題すべての場合を調べ尽くすことができないからといって、何も推論しないというのでは現実の様々な問題を解決できません。そこで、論理的思考において、現実的に帰納法を用いるための方法として次のものが挙げれます。
最初に、すべての前提が真であるとは言えない場合について考えます。
つまり、前提を調べる過程の中で偽である個別的・特殊的・具体的なものが見つかってしまう様な場合です。
簡単な方法として、先程紹介したものですが、結論で例外を認め、それを除いた形や条件を設定した形にすることです。「すべて」を使わずに「ほとんどのSnはPである」や、例外を排除した形である「あるS1を除いて、すべてのSnはPである」等のようにしておけばよいでしょう。
または、議論の最初に何について論じているか絞りをかけておくことも有効です。一々例外や条件を含んで結論を長くしたくない場合には、最初から例外が入って来ないように、議論の範囲を限定しておき、言葉の定義を狭くしておく等の方法です。
例えば、あらかじめ「渡り鳥」について話すことを明示しておけば、「鳥は空を飛ぶ」と結論づけても正しいことになります。こうしておけば、この議論では「渡り鳥」について話すのだから、「鳥」といえば「すべての渡り鳥」のことであり、「ペンギン」や「ダチョウ」は含まないことが分かるからです。したがって、「ペンギン」や「ダチョウ」といった結論「鳥は空を飛ぶ」を崩壊させる前提を無視することができ、安心して結論「鳥は空を飛ぶ」とできます。
次に、すべての前提を調べ尽くしたとは言えない場合についてです。
この場合は、すべての場合を調べ尽くせなかったが、ある程度の数は調べたので、これは必要で十分な数の前提を調べたと言えるので、結論を導いてよしとする、ということになります。つまり、色々調べた結果、今現在の段階では、調べた複数の前提は正しいので、それから帰納法で推論される結論も正しいと仮定してしまって、議論を進めて行くことになります。
例えば、様々な「カラスの色」を調べた結果、調べた内で「すべてのカラスの色が黒い」ことが分かったとします。この世のすべてのカラスを調べたわけではないが、調べたカラスを複数の前提として、結論「カラスは黒い」を帰納法で推論します。これは世界中すべてのカラスを1羽も逃さず調べることはできないので、ある一定数を調べた段階で、結論を導いてます。
なお、後になって「白いカラス」が発見されたら、すべての前提が真であるとは言えない場合のように、結論の「カラスは黒い」は修正され、「ほとんどのカラスは黒い」や「中には白いものもいるが、カラスは黒い」になったりします。
議論や学問を行う際には、演繹法と同様に、帰納法を使うことも多いので、このように妥協して用いることとします。
まとめると、帰納法では、
結論を導くのに必要で十分な数の根拠となる個別的・特殊的・具体的な前提があれば、
例外の存在を議論のどこかで確認しておくか、
今現在の段階ではということを確認しておく、
ことをしておけばよいということです。
この帰納法の蓋然性の問題は、以後の帰納法の応用的な推論形式でしょっちゅう出てきます。また、第III部 実証と反証でも説明したいと思います。
もちろん、結論を導くには前提が明らかに少なすぎたりする等、帰納法を使って議論を進めて行くには無理がある場合もあります。そういうときは、それを指摘して、一般化・普遍化・抽象化することなく、個別的・特殊的・具体的事柄として、狭く議論していくようにしないといけません。
3 演繹法との絡み
日常で論理的思考を用いる際には、帰納法のみでは推論が飛躍していると感じる場合が少なくないです。帰納法で導かれている結論も、よく考えると隠れた前提があり、それと演繹法が組み合わさっていることが多々あります。
(5.2)を見てください。
| (5.2)次の推論の隠れた前提は何か。 <前提1> 一朗は足が速い <前提2> 一朗は打撃が良い <前提3> 一朗は守備が上手い [結論] よって、一朗は一流の野球選手だ |
すべての命題の主語は「一朗」で統一されています。
述語は一見するとバラバラですが、結論の「一流の野球選手だ」ということもあり、どうやら「野球」に関連性があると推測できます。
そして、「足が速い」かつ「打撃が良い」かつ「守備が上手い」ことは、「一流の野球選手」に関連性があることも分かります。
どうやら「足が速い」こと、「打撃が良い」こと、「守備が上手い」ことの3つの要素は、「一流の野球選手」であるための必要な条件だ、ということが読み取れます。
しかしながら、3つの前提からは「足が速い、かつ、打撃が良い、かつ、守備が上手い野球選手ならば、一流の野球選手である」であることが明らかではありません。野球をよく知っている人ならば、「足が速い」こと、「打撃が良い」こと、「守備が上手い」ことの3要素を兼ね備えていれば、「一流の野球選手」であることは確かに納得します。しかし、そうした野球に関する前提を知らない人にとっては論理の飛躍を感じてしまいます。つまり、理解できないということです。
こう考えると、隠れた大前提として「足が速い、かつ、打撃が良い、かつ、守備が上手い野球選手ならば、一流の野球選手である」というのが推論に用いられていること分かります。
画像クリックで拡大
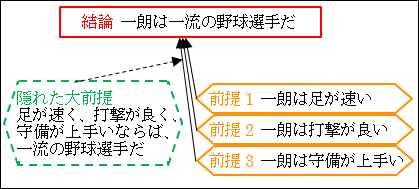
このように(5.2)は帰納法の推論の形式をとっていますが、分析してみると、明示された3つの前提だけでなく、もう1つ隠れた大前提を用いていることが分かります。
そして、隠れた大前提があることを見抜くと、帰納法だけでなく演繹法も使われていることに気付きます。
隠れた大前提として「足が速く、打撃が良く、守備が上手いならば、一流の野球選手だ」があります。そして、3つの前提は、「一朗」が「足が速い」、「打撃が良い」、「守備が上手い」と述べています。
これは、演繹法の1つ三段論法で、第2章 推論方法の基礎 5 条件法の前件肯定規則が応用された形式になっています。
| 前件肯定規則 <前提> P ⇒ Q <前提> P である (前件肯定) [結論] よって、Q である |
これに定言「S は P である」が組み合わさっています。
| 前件肯定規則+定言 <前提> P ⇒ Q <前提> S は P である [結論] よって、S は Q である |
「足が速く、打撃が良く、守備が上手い」を前件「P」とします。
「一流の野球選手だ」を後件「Q」とします。
「一朗」が主語の「S」です。
| (5.2)次の推論の隠れた前提は何か。 <前提1> 一朗は足が速い <前提2> 一朗は打撃が良い <前提3> 一朗は守備が上手い [結論] よって、一朗は一流の野球選手だ <隠れた大前提> 足が速く、打撃が良く、守備が上手い ⇒ 一流の野球選手だ <前提> 一朗は足が速く、打撃が良く、守備が上手いである |
これは、図4.3.演繹法の論理構造で示した形式の推論になっています。
図4.3.演繹法の論理構造
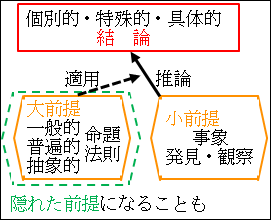
つまり、隠れた大前提が「P ⇒ Q」という一般的・普遍的・抽象的な命題になっており、それを、発見・観察された事象に適用して、個別的・特殊的・具体的な結論を導く、という演繹法の形式となっています。
今までの話をまとめて、どこで帰納法が使われており、どこで演繹法が使われているのか明確にしてみましょう。
最初に、帰納法を使って推論しています。
3つの前提「一朗は足が速い」、「一朗は打撃が良い」、「一朗は守備が上手い」から、
帰納法で推論して、
「一朗は足が速く、打撃が良く、守備が上手い」という1つの命題を結論として導く。
画像クリックで拡大

次に、演繹法を使います。
先程導いた結論「一朗は足が速く、打撃が良く、守備が上手い」を新たに前提と考えて、
この前提と隠れた大前提「足が速く、打撃が良く、守備が上手いならば、一流の野球選手だ」とから、
演繹法で推論して、
「一朗は一流の野球選手だ」という最終的な結論を導く。
画像クリックで拡大
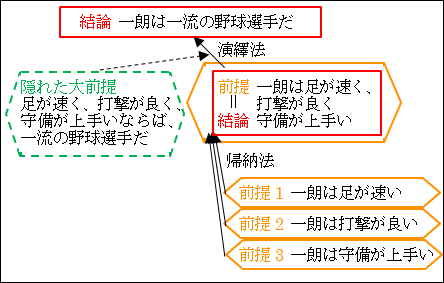
こうして見ると、最初の論理構造よりも詳しくなるので、論理がどこで飛躍しているのかが分かります。

今、飛躍と言いましたが、これは議論をする相手の知識量によるのは言うまでもありません。
野球に詳しい人なら、隠れた大前提すら言わずとも、3つの前提からいきなり結論を帰納しても構わないでしょう。もし、野球に無知の人なら、隠れた大前提を省略せずに明示しておく方がいいでしょう。
今回の推論は簡単なのでこれで十分かもしれませんが、相手の知識量が余りなく、さらに議論が複雑になっているなら、帰納法で出した結論を一度明示して、それを前提として、組み合わされる隠れた大前提を明示して演繹するのがよいことが分かります。
また、文章や議論で理解できない箇所があれば、このように演繹法と帰納法を駆使して与えられた前提から結論までの推論を分析してみることをお奨めします。
論理が飛躍していると感じる箇所について、根拠となる前提を1つ1つ確認して、帰納または演繹をして前提となる結論を導いたり、隠れた前提を見つけ出していきます。こうすれば、ある程度は論理展開に付いて行けるようになります。特に現代文が苦手な人は、一文一文をバラバラにして論理構成がどうなっているのか確認してみると力が付きます。
それでも分からない箇所は、知識が圧倒的に不足している可能性が高いです。ですから、その分野の知識を他の本や人にあたって調べたり勉強して補充する必要があります。
知識不足が問題でないとしたら、相手の推論または根拠たる前提が、間違えていることになります。この場合は、説得を試みたとしても無理強いはできないので、最終的に相手が修正するしかありません。
このように議論や学問は、演繹法と帰納法が複雑に絡む合いながら、前提から結論を導き、その結論が新たに前提となり、他の前提とともにまた新たな結論を導くといった形で論理が展開していきます。どちらかの推論方法の一方だけで済むことは滅多にありません。
例えば、(5.2)がこれが正しい推論と呼ぶには、隠れた大前提が真であることが必要です。
元々用いている3つの前提は確認された事実ですから、これが真であるのは問題ないです。そうでないとそもそもこの帰納法による推論が誤りになってしまいます。
3つの前提が真だとして、(5.2)の推論が正しいと言うためには、隠れた大前提が真であることが当然に必要とされます。
では、「足が速く、打撃が良く、守備が上手いならば、一流の野球選手だ」という隠れた大前提が真であることは、どう証明するのでしょうか。
予め正しいものとして扱っていますが、この隠れた大前提も元をたどれば、帰納法で推論されたものです。
長期間かつ大人数の個別的・特殊的・具体的な野球選手を観察して来て、「足が速く、打撃が良く、守備が上手い野球選手」が「一流」と呼ばれるていることを発見したとします。これを帰納法で推論して「足が速く、打撃が良く、守備が上手いならば、一流の野球選手だ」という一般的・普遍的・抽象的な命題を導き出しています。
そして、この元々帰納法で推論されたはずの命題は、(5.2)の「一朗」について述べる時には、もう一般的・普遍的・抽象的な命題として正しいものとして扱われています。つまり、帰納法で大前提が正しいことを証明することなしに、正しいモノとして演繹法の大前提として使われているわけです。
このように、論理的思考では、演繹法と帰納法は相互に補完します。したがって、演繹法と帰納法の両方が正しく使えることが、論理的思考の基礎と言えます。
4 演繹と帰納の比較
演繹法と帰納法の両方が、論理的思考で重要な推論方法であり、どのように組み合わされているかがよく分かったかと思います。そこで、演繹法と帰納法を比較してまとめてみます。
まず、改めて図4.1.を見てほしいのですが、抽象化と具体化を図示したものです。
具体的な概念 A1、A2、A3、…があり、それらに共通する性質が要素 a です。一部には共通するが、すべてには共通しないその他の要素は b、c、d、e、f、…です。
抽象的な概念 A には、要素 a があります。
図4.1.抽象化と具体化 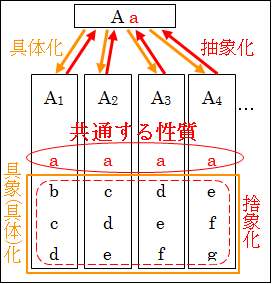
抽象化とは、具体的な概念から A1、A2、A3、…から共通する性質の要素 a を抜き出すことでした。抜き出す過程で、具体的な概念 A1らが持つ要素 b、c、d、e、f、…は無視されますが、これを捨象化と言いました。このように、具体的なモノから共通要素のみを取り出してそれ以外の要素を捨象化した結果として導かれるのが、抽象的な概念 A とその要素 a でした。
これは帰納法と同じであることが分かります。つまり、複数の個別的・特殊的・具体的な前提から、一般的・普遍的・抽象的な結論を導いているのと同じことだということです。
逆に、具体化では、抽象的な概念 A とその要素 a から、共通する性質の要素 a を持った具体的な概念 A1、A2、A3、…を導くことでした。もちろん、具体的な概念 A1らには、それぞれ共通しない要素 b、c、d、e、f、…が現れることになりますが、これを具象化と言いました。具象化は具体化と言ってもかまいません。このように、抽象的なモノをより具体的なモノにしてそれ以外の要素も具象化した結果として導かれるのが、具体的な概念 A1、A2、A3、…です。A1、A2、A3、…は、共通する性質要素 a を持っており、共通しない要素 b、c、d、e、f、…もあります。
これは演繹法と同じであることが分かります。一般的・普遍的・抽象的な前提から、個別的・特殊的・具体的な結論を導いているのと同じことだということです。
ただし、具象化された共通しない要素 b、c、d、e、f、…については、何も述べていないので注意してください。只々、具体的な概念 A1、A2、A3、…は、共通する要素 a を持っていることを述べているだけで、具体化にあたって共通しない要素 b、c、d、e、f、…が付いて来たとしてもそれ以外については何も述べていないということです。
図5.1.抽象・帰納と具体・演繹 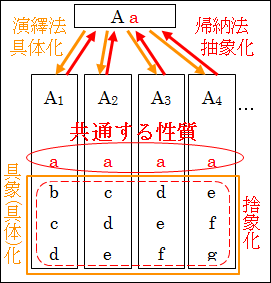
このことから、演繹法と帰納法の関係は、具体化と抽象化との関係と同じであり、論理の流れが逆になっていることが理解できたかと思います。
論理の流れが分かったところで、次にその論理の結果の正しさについて考えてみたいと思います。つまり、推論で導かれる結論が常に真であるかどうかということです。
演繹法では、三段論法に代表されるように、前提が真で、推論も正しければ、必然的に結論が真になりました。
帰納法では、前提が真で、推論が正しいとしても、必然的に結論が真になるとは限りませんでした。
図5.3を見れば分かりますが、演繹法および具体化の流れでは、抽象的な概念 A の要素 a から、それを具体化したものである具体的な概念 A1、A2、A3、…に要素 a があることを導いています。新しいことは特に何も言ってません。したがって、演繹法による推論の結論は当然に真となります。
帰納法および抽象化の流れでは、具体的な概念 A1、A2、A3、…から共通する要素 a を抜き出して、新しく抽象的な概念 A と共通する要素 a を導いています。しかし、前提をすべて調べ尽くすことが現実的にできないという問題がありました。したがって、本来は抽象的な概念 A に含まれるはずの具体的な概念 Ax なのに、共通する要素 a を含まないものが見つかる可能性が常にあります。つまり、調べ尽くしていないのに調べ尽くしたものとして推論するので、一種の飛躍があるというコトになります。したがって、帰納法による推論の結論は真になることもあれば、真にならないこともあります。真である確率が高いという蓋然性の高さしか言えませんでした。
図5.2.演繹・帰納法のまとめ 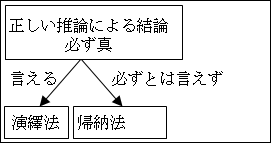
それでは、結論が真であるかどうかの保証に関連して、結論の情報量が増えるか否かを考えてみましょう。
抽象的な概念 A は、元々具体的な概念 A1、A2、A3、…から共通する性質 a を抜き出したものです。帰納法と言ってもいいです。
ということは逆に、演繹法で抽象的な概念 A を具体化したら、元々の具体的な概念 A1、A2、A3、…に戻るだけです。
つまり、結論の情報は、元々前提に含まれている情報を具体化しただけなので、結論の情報量自体は増えないことが分かります。
例えば、(5.2)のように、帰納法の後の演繹法の段階を考えると、「一朗は足が速く、打撃が良く、守備が上手い」というある事象を観察して、これを前提として、結論「一朗は一流の野球選手だ」を推論していますが、「足が速く、打撃が良く、守備が上手いならば、一流の野球選手だ」という大前提に含まれた内容でしかありません。
そして、具象化された共通しない要素 b、c、d、e、f、…については、推論過程では触れていないので、情報量が増えたわけではありません。
例えば、「足が速く、打撃が良く、守備が上手いならば、一流の野球選手だ」という一般的・普遍的・抽象的な大前提から、個別的・特殊的・具体的な「一朗は一流の野球選手だ」というの推論したとき、「一朗」については「足が速く、打撃が良く、守備が上手い」以外ににも、「一朗」に固有の「背が高い」や「筋肉質である」といった性質が当然にあるわけです。しかし、推論では「背が高い」や「筋肉質である」といいた性質には触れられていません。このことからも、推論の中では、結論の情報量は、前提の情報量を超えていないことが分かります。
このように演繹法では、元々前提に含まれている情報以上のものは出て来ず、結論の情報量自体は増えません。
しかしならがら、帰納法の場合には、情報量が増えます。
具体的な概念 A1、A2、A3、…から共通する性質 a を抜き出して抽象的な概念 A を導くときに、前提には含まれていない情報が、結論で追加されることが多いです。
例えばば、「あるカラス A1 は黒い」「あるカラスは A2 黒い」と、個別の「カラス」を観察して帰納すると、「すべてのカラスは黒い」となります。しかし、何度も言ってきたように、「すべてのカラス」を実際に観察することは現実的に無理があるので、「すべてのカラスは黒い」ことは正しいことを完全に証明ができないはずです。本来ならば「あるカラス A1、A2、A3、…は黒い」としか言えないところを、帰納法では「すべてのカラスは黒い」としています。これが許容されるのは、蓋然性が高いことに依存しています。もちろん、現実にすべての前提を調べ尽くせたのなら、特に新しい情報を持っているとは言えませんが、そうではない場合は、個別の「カラス」についてしか述べていない前提から、結論では「すべての」という新しい情報が追加されています。
このように帰納法では、元々前提に含まれている情報以上のものを含み得るので、結論の情報量自体は増えます。
図5.2.演繹・帰納法のまとめ 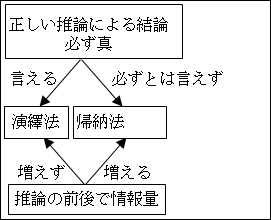
そして、演繹法と帰納法の特徴を見ると、次のようなことが言えます。
物事を分析する際に、論理の正しさを確認するときには、演繹法が非常に役に立ちます。演繹法なら前提が真であると仮定して、推論を正しく行えれば、結論は必ず正しくなるからです。しかし、演繹法では、論理の正しさは保証されても、前提の内容を超える結論を導くことができません。またそれ故に、最初に真であると仮定する前提を新しくつくり出すこともできません。
そこで、新たな命題や法則を創造する場合には、帰納法が活躍することになります。もちろん、蓋然性の問題、確からしさによって、議論の妥当性等は左右されますが、何か新しい結論を導いたり、必要な前提をつくる等のときには役に立ちます。
5 応用
帰納法が、前提の内容を超える結論を導けるとはいえ、複数の個別的・特殊的・具体的な事象を前提として、一般的・普遍的・抽象的な結論を導くだけでは、中々新しい発想は出てきません。そこで、演繹法と帰納法という2つの対立する推論方法を見てきたので、もう少しだけ演繹法と帰納法について考えていきます。
まず、改めて演繹法と帰納法を区別します。
三段論法に代表される推論の結果が必ず真となる推論方法を演繹法とします。
推論の結果が必ずしも真とならない推論方法を広義の帰納法とします。
広義の帰納法と言ったのは、理由があります。
今まで見てきた帰納法が、いわゆる世間一般で言われる帰納法です。この世間一般で帰納法と呼ばれているものは、枚挙的帰納法と呼んだりします。これを広義の帰納法に対して狭義の帰納法とします。
図5.2.演繹・帰納法のまとめ 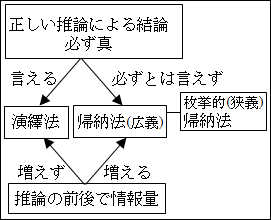
では、広義の帰納法とわざわざ呼ぶのだから、狭義の帰納法つまり枚挙的帰納法以外にも帰納法的な推論があるのだろうと察しがつくかと思います。
今から3つの
仮説推論
類比推論
弁証法
といった帰納法的な推論を学んでいきます。
ただし、類比推論を学んだ後に、弁証法にすぐには移らず、観念連合という思考の在り方の説明を学ぶことにします。その理由は、狭義の帰納法や仮説推論、類比推論がどうしてできるのか理解できるようになるからです。
図5.2.演繹・帰納法のまとめ 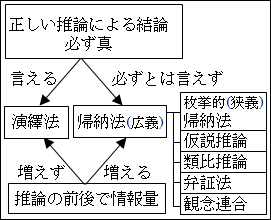
この分類方法は皆が皆必ずしも納得するモノではありませんが、この講義では論理的思考を行うためにという目的があるので、学問的な分類には余り突っ込まずに、演繹ではない推論方法を広義の帰納法とします。
前頁:第4章 演繹法
ページトップへ:第5章 帰納法
次頁:第6章 仮説推論