LAAD|第28章還元主義・総合・全体論

第28章還元主義・総合・全体論

学問と科学の大枠である観察―仮説形成―仮説検証と、定性的研究と定量的研究、実証主義と反証主義を学んできました。これで、学問と科学がどのように行われ、なぜ正しいのか、その正しさの限界は何かが理解できました。

そして、実際に研究をするときには、分析と総合によって進められることになります。これで対象が理解できると担保しているのは、「分解すれば理解できる」という要素還元主義という考え方です。しかし、要素還元主義にも問題があり、それを指摘するのが「全体は全体として捉えるべき」という全体論です。この2つを学ぶことにします。

目次
1 思考と道具のまとめ
 2 要素還元主義
 3 総合
 4 全体論
 5 まとめ

テキストのダウンロード［詳細］
通常版既述版

ADs

1 思考と道具のまとめ

これまで、学問と科学について学んできました。
学問と科学の目的は、真理の追究にありました。
そして、学問と科学は、観察―仮説形成―仮説検証という科学的方法の手順を踏まなければなりませんでした。モデルで考えることが効果的です。
さらに、対象をどのように研究するかという研究内容あるいは研究の性質の観点から定性的研究と定量的研究があることを学びました。

そうした科学的方法に則って定性的・定量的に研究して、仮説や理論を科学的に正しいと証明するためには、実証と反証の考え方が大切になります。事実と合致していることを実証するのに検証可能性と、間違っていることが証明できるという反証可能性とが重要でした。そして、学問・科学であるからには、反証可能性が必要になります。

以上が、学問的・科学的であることの条件でした。

それでは、実践段階、つまり、実際に対象を研究する段階では、具体的に何をどうすればいいのかという問題になります。
これについては、細かく見れば、学問と科学の各専門分野で異なってきます。ですから、この講義では、各分野に応じて何をどうすればいいのかという指導は一々しません。と言うよりも、私にはできません。私も全分野のことを指導できる程、各分野に通じているわけではないからです。

しかし、1つ言えることがあります。それは、どの分野であろうと、ほとんどすべての分野に共通するものがあります。
そして、その共通する方法は、研究する上で必要な思考法や分析の道具の基礎・基本は、既に第 I 部論理的思考と第 II 部論理的な問題解決で学びました。
思考法としては、演繹法・枚挙的帰納法(つまり狭義の帰納法)・仮説推論・類比推論・観念連合・弁証法がありました。
分析の道具としては、論理(ロジック)ツリー・因果関係図・論理ピラミッド(ピラミッドストラクチャー)がありました。

これらの様々な思考法を用いて対象を考えます。その思考に基づいて、分析の道具を使って対象を整理し理解します。
研究がどの分野であろうと、ほとんどすべての分野に共通した思考法と分析の道具です。もちろん、各分野に応じて、細かな違いがあり、思考法の何を重視するかや、道具の使い方が少し違ったりします。しかし、大筋では似たようなもので、共通しています。そういった意味では、一般的で普遍的で抽象的な思考法と道具だと言えます。

そして、現実の複雑な対象は、それ自体をそのままありのままに認識して理解することが不可能に近いほど困難でした。ですから、人間が理解できるように、複雑な対象を単純化して近似して再現したモデルを使って考えることになります。

このモデルを作るとき、実は、論理ツリーを使用するのと似たことをしています。
複雑で理解できない対象を、より具体的な要素に分解していきます。
分解された対象の各々の要素は、具体的になっており、理解できるほどに単純化されたものになります。複雑な対象自体をそのまま理解することは困難ですが、分解された単純で具体的な各々の要素をすべて理解すれば、複雑な対象全体が理解できるということになります。

こうした、全体を理解するのに、個別の部分の要素に分解して考えることを還元主義とか要素還元主義とか言ったりします。
そして、この(要素)還元主義の考え方は、論理ツリーが対象をどんどん具体的な要素に分解していく道具であることと似ているのが分かります。

なお、分解された要素の間に、因果関係があればどのような因果関係になっているかを考えることになります。
そのとき、因果関係の構造を可視化して理解を助けてくれる道具が、因果関係図になります。

こうして、色々なモデルが作られて、様々な対象を科学的に理解して行くことができます。
そうすると、複数のモデルを組み合わせたり、統合したりすることで、より分かり易いモデルや、より多くのことを説明できる理論を考えついたりします。
分解された要素を元の対象に再構成することを総合といいますが、別々のモデルを統一することも総合です。

特に、総合は、科学技術 technology と関係します。科学技術は、科学的に理解したことを複数同時に利用することがほとんどなので、総合する必要が生じやすいです。

この総合は、論理ピラミッドによる一般的で抽象的な結論に向かって個別的で具体的な事実やモデルを積み重ねて行くのと似ています。

こうして見ると、論理ツリーは要素還元主義という考え方を用いる際に役に立ち、因果関係図は科学の目的の中心の1つである因果関係の解明に役に立ち、論理ピラミッドは分解した上で全体を理解するために必要な総合という考え方を用いる際に役に立つことが分かります。
なるほど、分析の道具は、非常に科学的だったわけです。

少し前置きが長くなりましたが、このように、要素還元主義と総合という考え方が、学問と科学では役に立ち対象の理解を助けてくれます。
しかし、要素還元主義と総合で対象を完全に理解できたと考えてしまうと、問題があるのも事実です。それを教えてくれるのが全体論です。
今回は、要素還元主義・総合・全体論について順に学ぶことにします。

ページトップへ

2 要素還元主義

複雑で理解困難な対象も、具体的な要素に分解して単純なものにすれば、理解できる。
これは非常に納得しやすい考え方かと思います。

学校の勉強で問題を解くときも、問題文を細かく要素ごとに分解して、分解した要素を個別的に検討しているはずで。これは、この「分解すれば理解できる」という考え方に基づいたものだと言えます。
学問と科学でも、仮説を形成したり概念を構築したりするとき、対象を構成する要素が具体的に何なのかを考えています。

このように、抽象的な概念や対象を、具体的な要素に分解して理解する立場を要素還元主義、あるいは、単に還元主義と言います。

英語では、reductionism と言います。
reduce が「減らす」という意味で、これと名詞化する -tion が組み合わさって、reduction となり「減少」となります。さらに、reduction に「主義」を表す接尾辞 -ism がくっついて、reductionismとなります。
複雑な対象を単純な具体的な要素に分解するときに、その複雑性を「減らしている」ことが分かります。
ちなみに、数学で、2/4＝1/2とすることを「約分する」と言いますが、英語では reduce を使います。

また、「還元」という言葉の意味が、「物事の元の形・性質・状態に戻すこと」を意味するので、要素還元主義とは、複雑な対象を基礎的で具体的な元の要素に戻す思考だと理解することもできます。

この要素還元主義は、科学で用いる分析と相性が良いことが分かります。
第 I 部第9章弁証法 3 総合・分析・直観でも説明しましたが、分析 analysis とは、複雑な対象をより単純な要素に分解して明らかにすることでした。

要素還元主義では、複雑で理解困難な対象も、具体的な要素に分解して単純なものにすれば、理解できると考えているので、具体的な要素に分解することが目指されます。
そして、それを実行するのに、複雑な対象をより単純な要素に分解して明らかにする、すなわち、分析するのです。

こうして、要素還元主義に基づいて分析をすれば、分解された具体的で基礎的な要素を個別に理解することで、結果として、複雑な対象の全体像が理解できるようになります。

そして、対象を具体的な要素に分解するときに、何の道具を使ったかと言えば、論理ツリーでした。
論理ツリーにも色々な使い方がありますが、トップダウン(逆算)方式で、抽象的な概念や対象から、具体的な要素に分解していくのに特に適していました。
したがって、論理ツリーは要素還元主義と分析に最適な道具だということが分かります。
なお、具体的な要素に分解した後に、対象の構造を掴むために因果関係図が用いられることも多いです。

以上で、学問的・科学的な研究では、要素還元主義の考え方が大変有益なことが分かります。

例えば、学問の分類、専門分野の分類は、要素還元主義の考え方に基づいています。
理科系の学問とかよく言われる、物理、化学、生物などを例にとって説明してみましょう。
「理科系の学問」は「自然現象についての学問」と説明できますが、抽象的で捉えどころが中々ありません。

理科系の学問：自然現象についての学問

要素還元主義に則って、「理科系の学問」を具体的な要素に分解してみると、「物理」「化学」「生物」「地学」と具体的な学問に分解できます。
そうすると、「理科系の学問」がどういったものかが、「物理」「化学」「生物」「地学」という学問を理解することで分かって来ます。
図28.1.理科系の学問

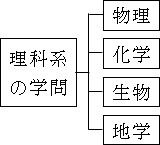
なお、さらに、具体的な要素である「物理」は、「力学」「電磁気学」「熱」等々とより具体的な要素に分解していくことができます。「化学」等も同様です。
どこまで具体的な要素に分解していくかは、対象をどう理解したいかという目的によりけりになります。
こうして、理解困難な対象は、分解された具体的な要素を理解することを通して、理解することができます。

このように、要素還元主義は、学問と科学の1つの支柱になっています。

補足として、要素還元主義という言葉に「主義」が入っていますが、思想などのように、特定の原理を信奉することを必ずしも意味しているものではありません。
つまり、還元主義以外の立場を否定したり批判したりするわけではありません。そもそも、学問と科学においては、分析は避けて通れません。他の有効な方法論が提唱されない限り、分析なしに何かを理解することは、今の所、難しいです。
ですから、自分は「主義」に囚われないと考えずに、演繹法や帰納法のように、一つの便利な思考法として受け入れてください。

ページトップへ

3 総合

要素還元主義と分析によって、対象を具体的な要素に分解して理解したら、分解した要素を再度まとめ直します。これを総合 synthesis と言いました。つまり、総合とは、分析の結果として得られた要素を統一して構成することです。

分析して総合することで、対象を理解できます。

と言っても、まぁ、バラバラにしたものをバラバラにしただけで満足して終わらす人は珍しいでしょうから、総合と言われても当たり前だと思うかもしれません。
分析したからには、大なり小なり総合をすることにはなります。敢えて総合という考え方を持ち出したのは、分断された知を統合するのに必要だからです。
この総合は、科学技術 technology に応用するときに効果を発揮します。

まず再度の確認ですが、分析を通じて、様々な対象を理解していくと、知識が蓄積されていきます。でも、その知識はバラバラのままです。
1つ1つ個別の知識は分析を通じてよく理解できています。しかし、その1つ1つの知識は、別々の分析を通じて得られたものです。そのため、相互の関係性がよく分かりません。
ですから、知識同士の相互の関係性を明らかにして、統一的あるいは法則的に理解したいと考えます。
また、統一的・法則的な理解ができれば、知識が体系化されて、非常に論理的になり、個々の知識の理解自体も深まります。

個別の知識や事実を並べて、何が言えるのかを考えます。あるいは、その個別の知識や事実を支配する一段上の抽象的な法則や概念はないのか、とも考えます。
こうして総合化を試みることで、相互にバラバラな要素が、互いに関係性を持ちながら、統一的に構成されていきます。

何故こうした総合化が、科学技術への応用に繋がるのかと言えば、別々の知識を関係付けて用いるためです。
科学技術 technologyは、科学的な知を応用する方法です。主に工学や産業に関する場面で用いられます。

「科学と技術」と一まとめにして述べるときのように、単に「技術」と呼ばれることもあります。
この「科学と技術」の言葉の使い方は、「科学」が純粋に真理の追究を目的としていることと対比して、「技術」の「科学」を応用して役に立てることを目的としている点を強調しています。

科学技術が総合であることについて、電気の発電を例にとって簡単にですが見てみましょう。
なお、中学校レベルの物理で説明するので、「ぼく、りかのこと、よくわからない」という人も安心してください。中学生でこれから習う人は、へぇと思いながら聞いてください。中学を既に卒業したのにこの説明が分からない人は、義務教育を全うできなかった人なので、その事実を真摯に受け入れて、後で勉強し直しておいてください。

発電は、何らかのエネルギーを電気エネルギーに変換することです。
発電は、私達の生活に必要な電力を手に入れるために行います。

では、発電を行う機械である発電機は、どのような仕組みで動いているのでしょうか。

発電機は、大きく3つによって構成されています。磁石、コイル、タービンです。
コイルとは、針金等を螺旋状に巻いたものです。
タービンとは、回転運動すための軸に羽根がつけられたものです。
図28.2.発電機の仕組み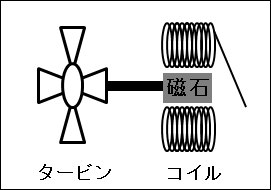

発電機は、コイルに対して磁石を回すことで電気を発生させます。
コイルとは、針金等を螺旋状に巻いたものです。
このコイルに磁石を近づけたり遠ざけたりすると、電極が変わり、電流が発生します。
こうした現象を、電磁誘導と言います。これは物理現象の1つです。
電磁誘導によって、電気エネルギーが獲得できます。

したがって、コイルに対して、磁石を回せば電気が得られるので、磁石を回したいと考えます。
そこで、登場するのがタービンです。

タービンとは、回転運動すための軸に羽根がつけられたものです。
羽根に風などが当たれば、羽根が風に流されます。
そうすると、回転軸が羽根につられて回ることになります。
タービンが回転するときに生じているのは、運動エネルギーです。
言うまでもありませんが、運動エネルギーとは、運動に伴うエネルギーです。これも物理現象の1つです。
図28.2.発電機の仕組み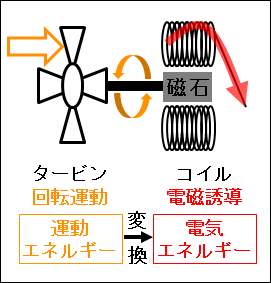

よって、発電機の磁石とタービンの回転軸を繋ぎます。
そうすると、タービンの羽根に風などを当てて、運動エネルギーを使って回転軸を回します。
回転軸が回れば、それに繋げられた磁石も回転します。
そうすると、電極が回転する度に切り替わることになります。
電極が切り替われば、コイルに電流が発生します。これで電気を得られることになります。
こうして、運動エネルギーから電気エネルギーを得ることができます。
図28.3.回転運動と電磁誘導と総合画像クリックで拡大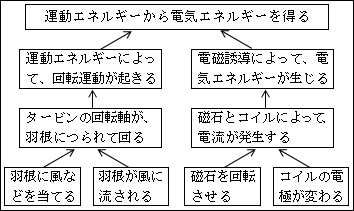

このように、本来はバラバラである「電磁誘導という物理現象」と「回転運動という物理現象」を関係付けて総合することで、私達の生活に欠かせない電気を得る技術 technology を開発することができました。

なお、最初のタービンを回すための運動エネルギーは、どうやって作りだすのか、と思った人もいるでしょう。その方法は色々です。
火力発電ならば、典型的なのは、石油や石炭といった化石燃料を燃やす方法です。
水を沸騰させて水蒸気を生み出して、タービンを回します。この場合、化石燃料を燃やすので、化学反応の熱エネルギーを利用することになるので、物理だけではなく化学の知識も必要になってきます。

他にも水力発電や風力発電があります。
水力発電なら、水の流れる力を利用してタービンを回します。よくダム等で利用されており、ダムの水が高い所から低い所へ流れるときの位置エネルギーを運動エネルギーに変換して、タービンを回します。
風力発電なら、簡単でタービンの羽根に風を当てればいいので、風の運動エネルギーをそのまま利用できます。
今現在、時事で議論の的になっている原子力発電も基本は同じです。最初のタービンを回すためのエネルギー源として、原子の核分裂反応を利用しています。核分裂時に、物凄い熱が発生するので、その熱エネルギーで水蒸気を生み出してタービンを回します。
ですから、より詳しく言えば、「電磁誘導」「回転運動」「化学反応」といったものを総合していることになります。

このように、総合は科学技術を考案したり用いる際に非常に大切になります。
バラバラな科学的な知識を上手く組み合わせて統一することで、新たな発明を行うことができます。

以上、総合について説明して来ましたが、分析によって分解した要素を統一して再構築する場合でも、科学技術としてバラバラな科学的な知識を統一して応用する場合でも、別々の知識や事柄・事実を具体的な要素として、より一般的な抽象的なものへと統一・統合していることが分かります。

この総合化では、思考法や整理法の道具として、対象を一般的・抽象的に統一するために、論理ピラミッドが有効なのが分かります。
論理ピラミッドにもいろいろな使い方がありますが、ボトムアップ(積み上げ)方式で、具体的な事実から、抽象的な概念等へと統一していくのに特に適していました。
したがって、論理ピラミッドが総合に最適な道具であることが分かります。

ページトップへ

4 全体論

要素還元主義に基づいた分析と総合によって、学問的・科学的に、色々なことを理解でき応用することができると分かりました。これで、何か疑問に思うことがあっても、具体的な要素に分解して個別に理解して、総合すれば、対象を理解できる。もう何も怖くない。となりそうなのですが、1つ注意があります。

要素還元主義に基づいて分析し総合するとき、前提として、分解した具体的な要素を合せると全体を理解できるという考えがありました。
つまり、分解された具体的な要素を全部合わせると、そのまま全体になるという考えです。これは、特段、変ではありません。
5という数字を最小の正の整数に分解すれば、5=1+1+1+1+1となります。確かに具体的な要素1を全部合わせると、元の全体の5になります。

実際に対象を分析するとき、非常に狭い範囲、あるいは、比較的単純な構造である対象を分析するのならば、要素還元主義でも特段問題にならないように思えます。
しかし、複雑な体系やシステム等、その範囲を広げるとどうなるでしょうか。

例えば、人間の身体全部を理解しようとするとき、頭、顔、首、胸、腹、腕…と部分に分解して個別に理解することで、人間の身体全体を理解できたと言えるのでしょうか。
社会全体はどうでしょうか。経済全体もどうでしょうか。自然の生態全体はどうでしょうか。
こうした複雑な体系においては、何かを改善しようと思い、ある一部を変化させてみたら、思わぬ所に影響が出てしまうことがあります。そして、複雑な体系の中で、その影響がどのような経路を辿って生じているのかも明確には特定できない場合が少なくありません。

このように、「分解すれば理解できる」という要素還元主義では、結局、対象を理解できないのではないかと考えることができます。つまり、分解した具体的な要素である部分を理解することで、複雑な体系の全体を把握・理解することできない、ということになります。

したがって、体系とそれを構成する要素は、部分の集合としてではなく、全体として捉えるべきだという考え方が唱えられます。これを全体論と言います。「全体は全体として捉えるべき」という一言に集約されるでしょう。英語では、holism と言います。

holism の語源を辿ると、結構面白いです。
まず、holism の hol は whole と同じ意味で、「全体」とか「完全」を表します。
馴染み深い表現として the whole world で「全世界」という意味になるのは皆さんもよく知っているでしょう。地球上のすべての世界を表しています。
他に、ケーキでも、三角形に切られたケーキではなく、誕生日等でロウソクが立てられる1つ丸々のケーキをホールケーキと言いますが、あれも whole cakes で「ホールケーキ」ですね。
あとは、牛乳も色々な種類があります。脂肪分を取り除いた牛乳もあれば、特に何も手を加えていない牛乳もあります。後者の普通の牛乳、いわゆる「全乳」は、whole milk と言います。採れた牛乳がそのままの状態であることを表しています。

このように、hol と whole は同じ意味になります。そして、語源的には古代ギリシア語の holos に由来しています。
この holos は「すべて」とか「完全」といった意味を持っています。
もっと詳しく言えば、印欧語系の多くに共通している語です。

印欧語とは、インド＝ヨーロッパ語のことです。インドとヨーロッパの言語は元々1つ乃至、それに近いものだったのが、時代の流れと共に地域で変化していき、ドイツ語になったり英語になったりフランス語になったりしています。が、まぁ語学の講義でもないので、別にいいです。

さらに、whole からは、heal や helath という語も派生していきます。
heal は、動詞で「癒す・癒える」の意味が有名ですね。その名詞形である health は「健康」の意味で捉えられることが多いかと思います。
これらは、「完全な状態」が基本的で基礎的な、つまり、核心的な意味になります。

heal は「癒す・癒える」ですが、これは身体が持つ自己再生的な治療を意味します。
「完全な状態」に戻ることが heal なわけです。
heal を「治療する」と日本語に訳すと、cure との区別が日本語上では分かり難くなります。cure は外部からの治療によって「治る」ことが中心になります。cure が手当や処置などの外的な要因による治療であるのに対して、heal は人間の身体が持つ自己治癒だと言えます。
そして、health は「完全な状態」である身体なので、日本語で「健康」となりますが、治療も何も必要とせず、そのままで「完全な状態」であることが分かります。

さらに、whole、heal・health からは、holy「神聖な」という意味も引き出されていきます。
heal・health が欠けていることのない「完全な状態」を意味しており、これが原始的な宗教の「完全性」と結びついて、holy という語が形成されます。

原始的な宗教というのは、キリスト教ではありません。まだイギリス人とかに分化する前のゲルマン人の時代に信仰していた自然崇拝というか土着的な宗教です。
彼らは、キリスト教的な唯一神を信じていたのではなく、「熱い」と「寒い」という両極端から世界が生み出されたと考えていました。
具体的には、氷が熱によって溶けることで、「父なる天」と「母なる大地」に分かれて世界が形成されたと考えていました。

熱で溶ける前の氷、雹ひょうや霰あられ、雪の塊として、「卵」がイメージされます。
この「原初的な卵」が「神」のような存在であり、世界が分化する前の「完全な状態」あるいは「完全な存在」です。
それゆえに、不思議な「癒す」力があると考えられ、それは「神聖な」ものであると思われるようになります。

ですから、英語の hail は、名詞として「雹・霰」という意味がある一方で、動詞の「万歳する」や「歓迎する」といった意味があります。この背景を知らずに「雹・霰」という意味と「万歳する／歓迎する」という意味が同じ hail が持っていることに違和感を覚えるかと思います。が、古代ゲルマンの時代まで遡れば、そこまでおかしく感じずに納得行くものだと思います。

こうした原始的な宗教観は、イギリス人がキリスト教化された後も、キリスト教の唯一絶対の完全な「神」のイメージと結びつくことにそこまで無理がないので、holy という単語となって残って行きます。

こうした意味の広がりを持った whole「完全な状態」「全体の」という意味に、「主義」を意味する -ism とが組み合わさって holism という語はできています。

この holism を日本語に訳すのなら、還元主義と対の概念なので、「全体主義」とするのが妥当に思われます。しかし、日本語で「全体主義」というと、政治学や社会学で使う「全体主義」totalitarianism の意味で取られることが多いという問題があります。
したがって、holism は、そのままカタカナで「ホーリズム」と表すか、漢字に直して「全体論」とされることが多いです。

ちなみに、「全体主義」totalitarianism は、国家が個人と社会全体を制御、つまり、可能な限りありとあらゆる公私に関わる事柄のすべての領域を制御しようとする体制のことです。
今で言うなら、中国や北朝鮮のような共産主義国家を思い浮かべていただいたら分かりやすかと思います。
あれは厳密に言えば、国家ではなく共産党が社会全体を制御しているのですが、共産党が国家を支配、あるいは、共産党が国家と一体化しているので、細かい違いはまぁいいです。
国家が何でもかんでも簡単に規制でき介入でき、人民の生活から経済まで制御しようとしています。個人の自由は、全体の利益のために犠牲になることが強いられます。

ちょっと話が逸れ過ぎました。話を全体論 holism に戻しましょう。
このように、全体論では、体系とそれを構成する要素は、部分の集合としてではなく、全体として捉えるべきだと主張して要素還元主義的なものでは、体系全体を理解できないことを主張しました。

でも、現に、要素還元主義的な分析でも色々なことが明らかにできているのに、それを否定してどうするんだ、とも思えるわけです。
確かに、こうした問題は、直接論争している科学哲学者以外の者にはあまり関係ないように感じます。
しかし、学問や科学を修める者としては、分析と総合で色々なことが理解できたと思えても、安易に全体が理解できたと思ってはいけない、という戒めとして全体論を受け止めておくべきでしょう。

全体を要素に分解するときも、要素を全体に再構築するときも、重要ではないと考えられた要素は切り捨てられています。
それが本当に重要ではないことは、保証されていません。その分析や総合の仕方が、「科学的に正しい」ことは、今現在、反証されていないだけかもしれません。
ですから、「分析して総合した結果、理解した理論なのだから、これは絶対に正しい」、そう信じて、現実に対して無理に理論に当てはめようとしたり、現実を否定したりする行為は愚かだと分かります。
こうした全体論的な考えも心に留めておかないといけません。

こう説明すると、次は要素還元主義を徹底的に否定しだす人が現れて困るのですが、要素還元主義は要素還元主義で便利です。
複雑な体系全体を要素に分解することは難しいかもしれませんが、狭い範囲で対象を分析するのなら、あまり問題がない場合も多いです。

要は、道具は使い方次第です。
要素還元主義で分かることもあれば、全体論の立場から複雑な体系を複雑なまま何とか理解することが必要な場面もあるということです。

ページトップへ

5 まとめ

さて、観察―仮説形成―仮説検証という科学的方法の手順、そして、研究の性質としての定性的研究と定量的研究という枠組みの下に、今まで第I部と第II部で学んできた思考法とそれを実際に使うための道具が、学問的・科学的な研究方法にどのように関係しているのかを見ました。

「分解すれば理解できる」という考え方を表した要素還元主義に基づいて、分析と総合が学問的・科学的な研究の中心の柱となりました。それを具現化するのが、論理ツリー・因果関係図・論理ピラミッドでした。

そして、「分解すれば理解できる」という要素還元主義をより丁寧に説明すれば、抽象的な概念や対象を、具体的な要素に分解して理解する立場です。
しかし、分解した具体的な要素をすべて理解すれば、対象の全体を理解できるとは必ずしも限らないことも心得ておく必要があります。
複雑な体系を理解しようとするとき、体系とそれを構成する要素は、部分の集合としてではなく、全体として捉えるべきだという全体論の考え方があることを覚えておくことが大切です。

現代科学が過去と比べてもかなり発展しているような気がしても、要素還元主義で部分に分解してそれを理解したからといっても、全体が理解できたと確信をすぐに持たないように心掛けておかないといけません。

以上で、学問と科学にまつわる様々な方法論や考え方、捉え方を説明してきました。次からは、対象の特徴に応じて、学問がどのような専門分野に分類されているかを概観します。

前頁：第27章実証主義と論理主義
ページトップへ：第章28 還元主義・総合・全体論
次頁：第29章学問と専門・教養

第28章 還元主義・総合・全体論

1 思考と道具のまとめ

2 要素還元主義

3 総合

4 全体論

5 まとめ

総論 教養と学問の前に

第28章還元主義・総合・全体論

総論教養と学問の前に