前頁 |▼| 次頁
第15章 論理ツリー ― what ツリー―
論理(ロジック)ツリーは、「発生型」の問題を分析と解決策を立案するための道具です。この論理ツリーをこれから3章に渡って説明していきます。最初に、原因の特定や解決策を考える前の仕込みとして、論理ツリーが一体何なのかを理解するために、構造・概念の整理法から始めたいと思います。
| 目次 |
| 1 論理ツリーとは 2 MECE 3 枠組み 4 適切な枠組み設定 5 論理ツリーの作り方 6 ボトムアップ(積み上げ)方式 7 トップダウン(逆算方式)方式 8 まとめ テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 論理ツリーとは
論理ツリー、または、ロジックツリーとは、問題の分析や解決策を考える際に役に立つ道具です。
物事を効果的・効率的に考えるために、ある主題や論点を具体的な次元まで掘り下げることが主な使い方になります。
英語では、logic trees や issue trees と言われます。論理ツリーの「ツリー」は、英語の tree です。つまり「木」です。日本語で言えば、「論理樹」とする方がいいのかもしれませんが、論理ツリーやロジックツリーという呼び方が定着しているので、この講義では「論理ツリー」という呼称を使います。
「木」ということから、数学で学ぶ「樹形図」を思い浮かべてもらいたいです。木が枝分かれしているように、論理が枝分かれしていくイメージを持ってもらえると分かりやすいはずです。
実はすでに、論理ツリーについての考え方は、少しだけ触れています。第 I 部 第8章 観念連合 2 観念・概念・範疇で、範疇・カテゴリーで概念を分類していくときに使っています。「何か書(描)けるもの」で「鉛筆」等を分類していました。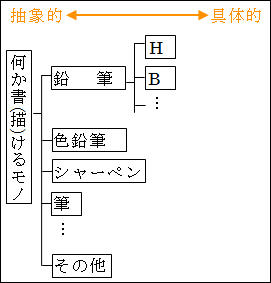
なお、範疇・カテゴリーという語句はこれからどんどん使うので、もう一度定義を確認しておきます。範疇あるいはカテゴリーとは、ある概念に応じて分類された物の集まりです。似た性質、同じ性質が含まれている範囲とも言えます。
また同じく、第 I 部 第10章 論理的思考のまとめ 2 講義の整理でも、推論方法をその特徴に応じてまとめましたが、これも論理ツリーを使ったまとめでした。
図10.1.推論のまとめ 画像クリックで拡大 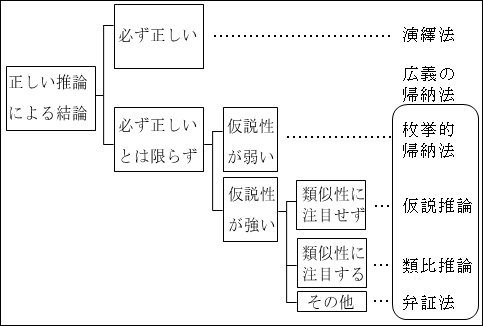
このように、論理ツリーは、左から右に行くにつれて、枝分かれしていくように描き表されます。
図から分かるように、一番左の箱は基本的には1つです。
ここには、最も抽象的な概念や命題が置かれます。
この箱をトップボックスと言います。
図15.1.論理ツリーの概念図 画像クリックで拡大 
そして、その右側にその命題や概念を具体的な構成要素に分けます。
分解される箱の数は、それぞれの概念や命題で異なります。
分解された命題や概念をさらに右側に分解していきます。
これを何度か繰り返していきます。何回繰り返せばよいかも命題や概念によって異なります。
図15.1.論理ツリーの概念図 画像クリックで拡大 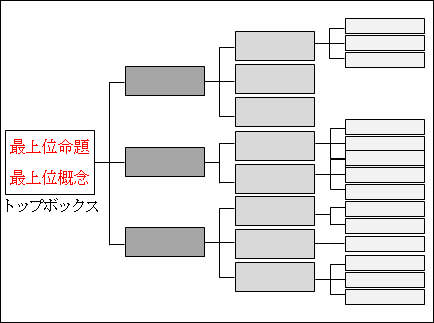
そうすると、一番左が最も抽象的な命題や概念であり、右に行くに従って、具体的な命題や概念になって行きます。
図15.1.論理ツリーの概念図 画像クリックで拡大 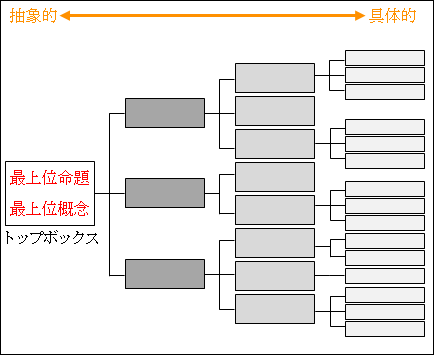
なお、各列には名前がついており、左から順に第1階層、第2階層、第3階層、第4階層…と呼ばれます。
図15.1.論理ツリーの概念図 画像クリックで拡大 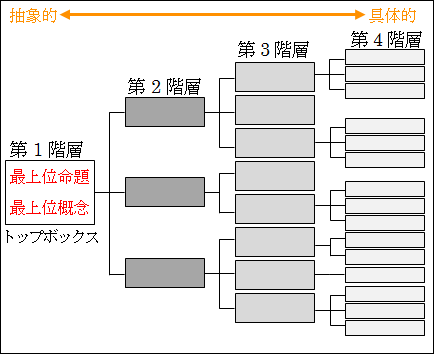
注意点としては、同じ階層内では抽象度の次元がそろうように分解しないといけません。
図15.1.論理ツリーの概念図 画像クリックで拡大 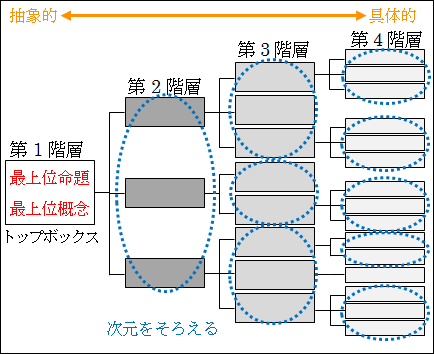
逆に言えば、違う階層同士を比べると、抽象度の次元が異なります。
左の階層の方が右の階層よりも、抽象度の次元が高いです。つまり、命題や概念が、左の階層にあればあるほど、それは高次の命題や概念となります。
このことからも、一番左の第1階層が、最上位命題、最上位概念となることが確認できます。
そして、抽象的な命題や概念を、より具体的な命題や概念に分解するとき、ただ漠然と分解していってはだめです。「分解することで、何をしたいのか」という目的を意識して分解して行きます。目的的達成志向です。他にも分解するときの規則がありますが、これは次節で紹介します。今は、分解するときは、目的達成志向が重要だということを心得てください。
図15.1.論理ツリーの概念図 画像クリックで拡大 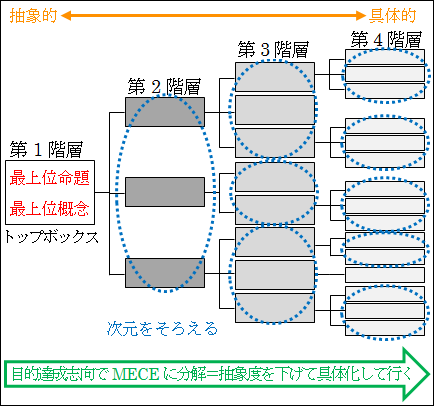
したがって、論理ツリーは、目的に応じて、what ツリー、why ツリー、how ツリーの3種類を使い分けることになります。
目的が「構造・概念の整理」のときには、what ツリーを用います。
目的が「原因の究明」のときには、why ツリーを用います。
目的が「解決策の立案」のときには、how ツリーを用います。
3種類あるといっても、基本的な論理ツリーの使い方はすべて同じで、目的達成志向によって、考えて行く方向が違うだけです。ですから、基本的な方法を習得してしまえば、あとは各場合に応じて使い分ける練習をすればいいです。
導入の終わりとして、論理ツリーを使うことの利点をおさらいしておきます。
目的達成志向で分解し整理することで、各命題や概念がどれだけ抽象的なのか、または、具体的なのかが、視覚的に分かりやすくなります。
また、各命題や概念のお互いの関係性も視覚的に把握できます。各命題や概念について、大きく見れば何に属しているのかも分かりやすくなります。
複雑な対象でも、様々な次元の各要素を見ることで、全体としてどうなっているのかの理解が進みます。
したがって、論理ツリーは、考察対象の全体像がどうなっているのか、対象の具体的な要素がどのような関係にあるのかを理解するための指針となる地図になっていると言えます。
最初に「構造・概念の整理」を目的とした what ツリーについて学びながら、論理ツリーの使い方を説明していきます。
先に紹介した「何か書(描)けるもの」と「推論」という2つの概念の整理は、この what ツリーを使っていたことになります。
2 MECE
論理ツリーの使い方として、目的達成志向で、抽象的なモノを具体的なモノに分解していくことの大切さが分かったかと思います。
しかしながら、もう1つ気を付けておかないといけないことがあります。構造・概念を正しく把握するためにも、問題を正しく認識するためにも、解決策を効果的に考えるためにも、分解された要素同士の関係に注意を払わないといけません。1.MECEとは
そのとき、重要で有効な考え方が MECE (ミーシー)です。人によっては、ミッシーと言ったりもします。
MECEとは、mutually exclusive collectively exhausitve の頭文字をとった略称です。
|
mutually exclusive は直訳すると、「相互に排他的である」という意味です。
collectively exhaustive は直訳すると、「全体として網羅的である」という意味です。
|
したがって、mutually exclusive collectively exhausitve は、「相互に排他的であり、全体として網羅的である」ということを意味します。直訳では硬く感じられるので、よく「モレなくダブりなく」と言われます。ただ、ここではMECEの語の順番を守るために、「ダブりなくモレなく」と言うことにしておきます。
|
何故に MECE で抽象的なモノを具体的な要素に分解していくのかについて考えてみましょう。
例えば、人間は、一生の中で年齢と共に健康に関わる状況が様々に変わります。
生まれて数年は免疫力も弱く、病気にかかると生命の危機に直結しやすいです。
成長するにつれて、身体も強くなり、病気にもかかり難くなってきます。
しかし、年をとって身体が衰え始めると、また病気にかかりやすくなったり、身体の至る所にガタが出てきます。
身体の発達段階に合わせて予防や治療が変わってくるので、年齢毎に分類することが大切になります。
日本人の平均寿命は男女で違いますが、だいたい80歳程度です。長いと、100歳以上生きる人もいます。とりあえず平均寿命でヒトの一生を考えましょう。
平均寿命まで生きるとしても、0~80まで81の段階があります。年齢毎に考えると、81の場合が考えられます。これはちょっと場合分けしているにしても、凄い数の場合です。81の場合を個別に考えるのは大変です。いくら年齢と共に発達段階が変わるとは言え、平均で81段階にも分けて各年齢の予防対策や治療法を考えるのは骨が折れます。
実際、これだけ細かく分けて対策を立てると、物凄い時間と金と人と物が必要になり、現実的に無理があることは、すぐ分かります。
そこで、厚生労働省は、年齢として81段階以上ある「人生」を「幼年期」、「少年期」、「青年期」、「壮年期」、「中年期」、「高年期」の6段階に分けています。
各段階に対応する年齢は、「0~5歳」、「6~14歳」、「15~30歳」、「31~44歳」、「45~64歳」、「65歳~」となっています。
図15.2.厚生労働省の人生の6段階
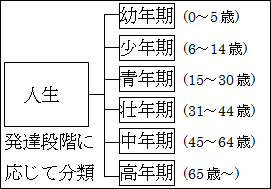
この分類は、「人生」、つまり、人間の一生という抽象的な概念を「ダブりなくモレなく」具体的な年齢や発達段階に分解しています。
こうすることで、大まかですが、各段階に応じて必要な注意点と予防を喚起でき、また、罹りやすい病気を中心に早期治療がしやすくなります。つまり、効果的で効率的に対策を立てられています。
「ダブりなく」分けられていることを確認してみます。
1つの年齢が1つの段階のみに属しています。
例えば、「15歳」を見てみましょう。「15歳」は「青年期」に分類されていますが、決して「少年期」には分類されているわけではありません。
確かに、各年齢が各段階に重複することなく分類されていることが確認できます。
「モレなく」分けられていることも確認します。
「高年期」が「65歳以上」なので、ズルく思えるかもしれませんが、0歳からすべての年齢が分類されています。
どの年齢も分類されていないということは決してありません。
確かに、各年齢のすべてを網羅して分類されています。
図15.3.人生の6段階のMECE
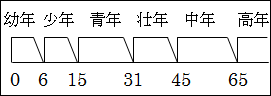
なお、数学では当たり前の表現ですが、図の数直線上に直角に交わっているのは、その数値を含んでいることを表します。斜めに交わっているのは、その数値を含まないことを表しています。
このように、MECE に(ダブりなくモレなく)分解することで、対象の全体がどういったものなのかを、具体的に過不足なく理解することができます。
2.ダブりがある場合 not ME
では、逆に「ダブりがある」場合ならどうなるでしょうか。例えば、次の図のように重複している箇所があるとします。
図15.4.人生の6段階のnot ME
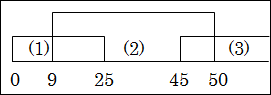
これは、第1段階を「0~25歳」、第2段階を「9~50歳」、第3段階を「45歳~」として分けた図です。
図からも分かる通り、(1)と(2)では「9~25歳」が重複しています。
さらに、(2)と(3)では「45~50歳」が重複しています。
どこが重複しているか分かりやすくするために、「9~25歳」の重複部分を赤色で、「45~50歳」の重複部分を黄色で塗ります。
図15.4.人生の6段階のnot ME
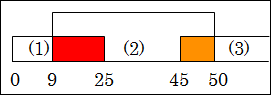
これは ME に反しています。つまり、mutually exclusive、相互に排他的になっていません。
そうすると、不都合な事態がいくつか生じます。
まず、「人生の段階」という対象理解が正確でありません。
このとき、「9~25歳」と「45~50歳」を2回数えています。これでは、一部の歳が1年だけではなく2年存在することになります。例えば、「25歳」は1年しかないのに、2年も「25歳」があることになります。
これでは、「1年に1歳を歳をとる」という規則を破っており、「人生の段階」の一部で「2年で1歳」となっています。
そもそも、人生を段階に分けているということは、そこに何かしらの共通する点があるわけです。それならば、重複している部分を、新しく段階(1.5)と段階(2.5)に分ける方がスッキリします。そうすれば、重複部分が2回数えられることもなくなります。
図15.4.人生の6段階のnot ME

また、他の不都合な事態として、非効率性が発生している確率が高いです。
もし、この人生の6段階が、問題解決のために分類されているとしたら、重複している部分に非効率が生じている確率が高いです。
各段階に応じて対策を立てる場合を考えてください。
段階(1)に相応しい対策 A、段階(2)に相応しい対策 B、段階(3)に相応しい対策 C を考え出します。
しかし、重複部分「9~25歳」では、対策 A と対策 B の2つを実施しないといけません。重複部分「45~50歳」では、対策 B と対策 C の2つを実施しないといけません。
図15.4.人生の6段階のnot ME
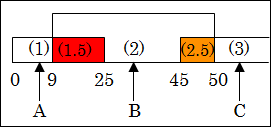
そもそも、対策 A は段階(1)に効果的なように、対策 B は段階(2)に効果的なように、それぞれ立案されているはずです。
しかし、重複部分「9~25歳」では、対策 A と対策 B の2つを実施するとなると、もっと効果的で効率的な1つの対策 D の存在の可能性があります。わざわざ2つの対策 A と対策 B を行うよりも1つの対策 D が考えられるのではないか、ということです。
これは重複部分「45~50歳」にも言えて、対策 E があるのではないかと言えます。
図15.4.人生の6段階のnot ME
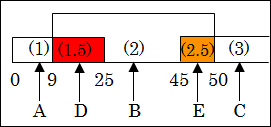
そう考えるならば、重複部分を新しく段階(1.5)と段階(2.5)に分ける方が、効果的で効率的な対策を実施できることになります。
このように重複した分類よりも、「ダブりなく」分類する方が、概念や構造を正しく把握でき、効果的で効率的な問題解決につながることが分かります。
3.モレがある場合 not CE
では次に、「モレがある」場合について考えてみましょう。例えば、次の図のように抜けがあるとします。
図15.5.人生の6段階のnot CE
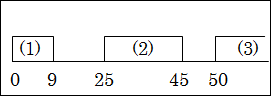
これは、第1段階を「0~9歳」、第2段階を「25~45歳」、第3段階を「50歳~」として分けた図です。
図からも分かる通り、(1)と(2)の間の「10~24歳」がどの段階にも属していません。
加えて、(2)と(3)の間の「46~49歳」もどの段階にも属していません。
どこが網羅されていないのか分かりやすくするために、「10~24歳」の部分を赤色で、「46~49歳」の部分を黄色で塗ります。
図15.5.人生の6段階のnot CE
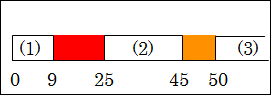
これは CE に反しています。つまり、collectively exhaustive、全体として網羅的になっていません。
そうすると、ダブりがあった場合と同様に、不都合な事態が生じます。
まず、「人生の段階」という対象の理解が正確になっていなません。
このとき、「10~24歳」と「46~49歳」が考えられていません。
「人生の段階」に、「10~24歳」と「46~49歳」が無いということは明らかな間違いです。
網羅されていない部分は、段階(1.5)と段階(2.5)として、ちゃんと網羅してやらないといけません。
図15.5.人生の6段階のnot CE
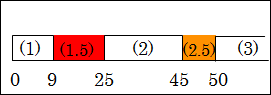
また、もしこれが問題解決のために分類しているとしたら、網羅されていない部分に何も対策が講じられないことになります。
なぜならば、網羅されていない部分は考えられていないからです。無いモノとして扱われています。最初から考えられておらず、無いモノとして扱われているから、分類に漏れが生じているわけです。ですから、当然に網羅されていない部分は、対策を考えるという発想に至りません。
逆に言えば、対策を考えているということは、そこに何かしらの集合を認めていることになります。
それならば、ちゃんと、「人生の段階」として、段階(1.5)と段階(2.5)といった具合に、網羅的に分類して表してやる必要があります。
そして、仮にこの段階で対策が不要ならば、最初の分類段階で弾くのではなく、ちゃんと網羅した上で、「段階(1.5)と段階(2.5)には対策は不要である」としてやります。
そうではないと、単に見落としていて気付いていないだけなのか、対策が不要なのかの区別ができません。特に他人に説明するとき、網羅されていない部分がある分類を示すと、おそらく質問されるはずです。「10~24歳と46~49歳の部分はどうした?」と。
また、論文や評論を読んでいると、
「A と B という問題がある。ここでは、B は~だから、論点を絞るために A について考えることにする」
といった文と出会うことが、よくあるかと思います。
こうすることで、筆者は、網羅的に分類をして、色々考えないといけない事柄があるのは理解しており、それを踏まえた上で、今回は A という論点に絞っていることを示しています。もし、これを怠っていきなり A について論じ始めたら、物をよく知っている読者に、
「B はどうした? もしかしてこの筆者は B について検討していないくらい浅い分析しているのでは?」
と思われるかもしれません。
筆者は、網羅的に分類していることを示すことで、反論されるのを予め防いでいるわけです。
このように、いったん網羅的に分けて、自分が見落としている部分がないことを確かめておくのが大切です。網羅されていない集合がある分類よりも、「モレなく」分類する方が、概念や構造を正しく把握でき、効果的で効率的な問題解決につながることが分かります。
以上、MECE、つまり、「ダブりなくモレなく」分解していくことの大切さが分かってもらえたかと思います。
3 枠組み
MECE で分解することが大切だと理解できたところで、1つ疑問が湧くかと思います。どうやったら MECE に分解できるのかという疑問です。ダブっていないことや、モレがないことをどうやって確かめればいいのでしょうか。ダブりなくモレなく分解する方法を学びます。1.枠組みとは
そこで役に立つのが枠組みです。枠組みは英語で、framework と言います。この英語を音写してカタカナで、フレームワークと言うことも最近は多いですね。
ここでの枠組みと呼んでいるものは、命題や概念を MECE に分解するための論理構造の枠組みです。
枠組みを設定することで、対象をどういった要素に分解すればよいのかが明確になり、考えるための指針となります。
図15.6.枠組み 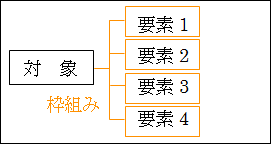
学問にしろ、経済活動にしろ、日々色々な研究がなされています。そして、様々な事柄が明らかにされて論理的に説明されて、枠組みが整理されています。そうした先人の知恵を有効に利用して、考える対象に応じて枠組みを適用すれば、正しく MECE に分解できます。枠組みは一種の知識ですし、専門家はこうした枠組みを整備したり、利用して物事を考えたりしています。
こうした研究の結果、整理された枠組みは、「ダブりなくモレなく」要素に分解できるように、論理的に構造が説明されています。
図15.6.枠組み 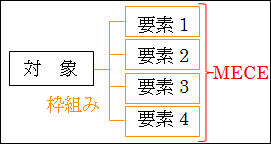
例えば、先程の「人生の段階」も厚生労働省が枠組みを提供してくれていると言えます。
厚生労働省は、「人生」を年齢と発達段階に応じて MECE に分解しています。確かに「人生」を「幼年期」、「少年期」、「青年期」、「壮年期」、「中年期」、「高年期」の6段階に「ダブりなくモレなく」分解できています。
もし年齢に応じた健康問題について考えたい場合には、この厚生労働省が用意している枠組みを使えば、上手くいく確率が高いと言えます。
そして、1つの命題や概念に適用できる枠組みは複数ある場合が多いです。
枠組みは、命題や概念をMECEに分解する論理構造の枠組みなので、枠組みが変われば、対象の理解の仕方も変わります。
つまり、枠組みの変更は、対象への切り口を変えること、あるいは、対象の見方を変えることと言えます。
したがって、対象をどう把握して理解したいかという目的意識によって、適用すべき枠組みが変わってきます。目的に応じて適用する枠組みを変えることを忘れないでください。
図15.6.枠組み 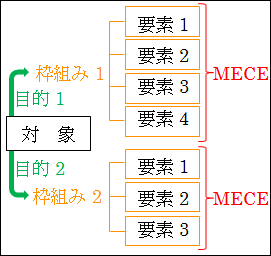
2.枠組みと対象の理解の変化
枠組みによって対象の理解が変わるので、目的に応じて適用する枠組みを変えることが大切な理由を事例を以って学びましょう。(15.1)を見てください。
| (15.1)高校では、「学問」は、その性質に応じて、「文科系」と「理科系」の2つに分けられている。しかし、大学では、「人文科学」、「社会科学」、「自然科学」の3つに分けられている。これは、同じ「学問」であるにもかかわらず、理解の仕方が異なっていることを意味する。その理由は何か考えよ。 (参考)人文科学・社会科学・自然科学の意味が分からない者は以下を参考にせよ。 文科系は、人文科学・社会科学 理科系は、自然科学 大まかには、このように理解してもらえればよい。詳しくは第III部 教養と学問・科学で説明する。 したがって、当問題は、高校では「文科系」「理科系」と2つに分類されるのに、大学では、「文科系」をさらに2つに割って、「人文科学」、「社会科学」、「自然科学」の3つに分類されるのは、何故かを考えればよい。 「枠組みによって対象の理解が変わること」と「目的に応じて枠組みを変えること」が鍵となる。 |
学問の分類法も枠組みによって見え方が変わってきます。
日本では、高校で文系か理系かを選択して大学入試に挑むため、学問も文系と理系に分けて考える人が多いです。ちなみに、文系は文科系、理系は理科系というのが正式な言い方で、文系も理系も略称です。
つまり、この文系と理系の選択は、学問を文科系と理科系に MECE に分解しているわけです。
図15.7.学問の分類法1
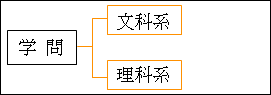
主に人間に関係する学問が文科系、主に自然に関係する学問が理科系に分類されます。
この文科系と理科系の枠組みを使って、色々な学問を分類して整理することで、学問の構造や傾向が理解できます。例えば、
法学は、人同士や社会の約束事を研究するのだから文科系に分類できます。
経済は学は、人や社会の経済活動を研究するのだから文科系に分類できます。
文学部は、描かれた人の生き方を研究するのだから文科系に分類できます。
工学は、自然の物質を使って、色々な技術を研究するのだから理科系に分類できます。
理学は、自然の法則や物質そのものを研究するのだから理科系に分類できます。
医学は、人間の病気という自然現象について研究するのだから理科系に分類できます。
図15.7.学問の分類法1
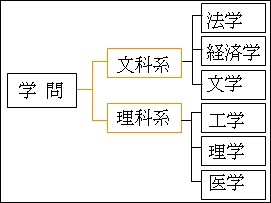
このように、学問を文科系と理科系に分けることで、広範囲に広がる様々な学問分野を何とか体系的に把握することができます。
大学入試でも文科系と理科系に分けられて、こうした学問を修めるのに必要な基礎的な知識として、教科や科目が設定されています。
しかしながら、学問を文科系と理科系の枠組みで分類・整理して理解するのは、かなり特殊で日本的です。
欧米では、人文科学、社会科学、自然科学の3つに分ける枠組みが一般的です(第III部 第30章 学問の専門分化)。
図15.8.学問の分類法2
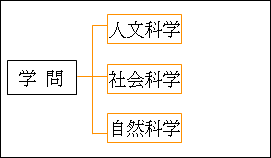
人文科学は、主に人間を研究する学問です。
社会科学は、主に人間関係つまり社会を研究する学問です。
自然科学は、主に自然を研究する学問です。
この枠組みを使って、様々な学問を分類することで、学問の構造や傾向が理解できるようになります。例えば、
法学は、人同士や社会の約束事を研究するのだから社会科学に分類できます。
経済は学は、人や社会の経済活動を研究するのだから社会科学に分類できます。
文学部は、描かれた人の生き方を研究するのだから人文科学に分類できます。
工学は、自然の物質を使って、色々な技術を研究するのだから自然科学に分類できます。
理学は、自然の法則や物質そのものを研究するのだから自然科学に分類できます。
医学は、人間の病気という自然現象について研究するのだから自然科学に分類できます。
図15.8.学問の分類法2
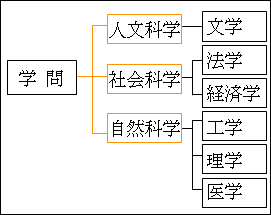
大学へ入って学問に触れれば分かりますが、文科系と理科系で学問を分ける枠組みよりも、人文科学と社会科学と自然科学で学問を分ける枠組みが用いられることの方が多いです。3つの科学に分類する方が、各学問の本質をより正確に捉えることができると言えます。
では、なぜ3つの科学に分類する枠組みの方が、欧米でも日本の大学でも一般的に用いられているのにもかかわらず、高校では文科系と理科系に分類する枠組みが用いられているのか。このことについて改めて考えてみましょう。
枠組みを使い分ける理由は、対象をどう把握して理解したいか、という目的が異なるからでした。
したがって、文科系と理科系に分類する枠組みと、人文科学と社会科学と自然科学に分類する枠組みとでは、学問をどう把握して理解したいか、という目的が違ってくることになります。
文科系と理科系で学問を分類するのは、大学入試で課す教科を決めるのに都合がいいからです。
文科系と理科系で大学入試で課される教科に、だいたいの傾向があります。
文科系なら国語と英語の2教科に、社会または数学で、合計3教科が主に課されます。
理科系なら英語と数学と理科2科目の合計4教科が主に課されます。
基本理念として、大学より前の高校段階では、大学の専門に分けて必要な教科に絞るよりも、基礎学力を養成し幅広く学ぶようになっています。これは、特定の専門に絞ると方向転換が難しくなるからです。18歳前後で進路を決定するのは、中々難しいものです。大学に入って、「何か思っていたのと違うなぁ」と感じる人は少なくありません。そのとき、もし専門を変えようとしても、特定の専門に絞った勉強をしていると方向転換はより一層困難になります。
例えば、数学が好きで数学を研究したいから、高校では数学だけ勉強したとします。
もし、こうした一芸にのみ秀でた人が大学に入って、「数学がやりたいことと何か違う」と感じて方向転換しようとしたとき、ほぼ不可能です。大学の講義は基本的に高校段階の内容は基礎として皆知っているものとして進むものなので、数学以外の内容が理解ができません。小学生に対して、中学段階を飛ばして高校段階の内容を教えても理解できないのと同じです。
また、文科系と理科系は、それぞれの学問の共通点を抽出することで、成り立っています。文科系と理科系に分かれていますが、その中の教科の内容は、どれも基礎的なものばかりです。したがって、大学で何の専門を学ぶにしても、高校で学ぶ教科の知識には、全てではないですが、多かれ少なかれ出会うはずです。
例えば、数学のみを純粋に研究する人はごく稀です。
数学を利用して物理現象を考えたりします。物理現象は、高校の物理だけでは終わることはすくないです。原子の動きや反応を考えるので化学も勉強しておかないといけません。したがって、高校段階の内容は基礎的な事柄なので、何かを専門的に研究しようとするときでも、どこからしらでその知識が必要になってきます。
このように、文科系と理科系に分類する枠組みで学問を理解する目的は、大学で本格的に専門を学ぶ前に、各専門に共通して土台となる基礎的な知識を身に付けるためだと言えます。
これに対して、人文科学、社会科学、自然科学に分類する枠組みで学問を理解する目的は、大学で各専門を学ぶためだと言えます。
こちらの分類の方が、文科系や理科系の分類よりも、学問を正確に理解しようと努めていると言えます。これは当然とも言えます。学問を修めるためには、学問とは何なのかをより正確に理解しておく必要があります。文科系・理科系は、学問を修める前の準備段階なので、そこまで正確さを求められておらず、細かい違いよりも大きく捉えることが大切だからです。
以上から、
| [解答] 大学入学以前の高校生に対しては、学問をあまり細かく分類するよりも、大枠を示すことで、色々な専門に通じる基礎を学ぶことの大切さを説く方が適切であるから、文科系と理科系の枠組みが用いられている。 これに対して、大学で学ぶ者に対しては、自分の専門が学問全体でどのような位置づけにあるのかを理解する必要があるため、学問をより正確に把握できるように、少し細かく分類する方が適切であるから、人文科学と社会科学と自然科学の枠組みを用いている。 |
こう説明できます。
なお当たり前ですが、解答がこの表現そのままでなくても結構です。
要点として、「高校段階では、基礎を理解するために大枠の理解が優先されているため」ことと「大学段階では、学問のより正確な理解が優先されるため」という2点を押えられていればいいです。
この(15.1)を通じて、目的に応じて枠組みが適切に選択されていることが理解できました。
そして、この例を通じて同時に、枠組みを変える、つまり、切り口を変えることで、対象の見方も変化していることも確認できました。
文科系と理科系の枠組みでは、学問は大きく見ると2つの系統があると理解しているのに対して、人文科学と社会科学と自然科学の枠組みでは、学問は大きく見ると3つの系統がある理解しています。
以上、対象をどのように把握して理解したいかという目的意識によって、適用すべき枠組みが変わることが分かりました。
同時に、適用すべき枠組みが変わると、命題や概念の理解の仕方が変わることも分かりました。
ですから、目的達成志向で、枠組み設定と MECE に分解するときに重要なのが分かります。
今、自分が何をしたいのかという目的意識を明確にして論理ツリーを使うことが大切です。what ツリーで概念を理解したいのか、why ツリーで原因を探求したいのか、how ツリーで解決策を考案したいのか。
これから始まり、より細かく具体的に何をしたいのかを考えます。
目的を達成するためには、どのような枠組みを設定して、対象を理解すればよいのかを考えます。
▼雑談を飛ばす
学問の分類に応じて、対象の理解の仕方が異なることを学んだついでに、学校の勉強と枠組みの関係についても少し触れておきます。
学校の勉強でも、枠組みを色々学ぶことになります。おそらく、枠組みという形で明確に提示されないでしょうが、様々な対象の理解の仕方を学びます。
この問題はこう考えると良いとか、
この事象はこう説明することができるとか、
こういった具合に勉強していると思います。これらは、対象をどう理解するかを勉強しているので、枠組みを学んでいると言えます。
ですから、学校の勉強をただの試験のための暗記物と考えては、もったいないです。対象を理解するための枠組みと捉えて、色々な対象に適用してみて、物事がどのように見えるのかを自分で試してみることが大切になります。
そう言えば、以前、ビジネスに興味のある生徒と話していると、少し勘違いしている人が何人かいたので、付け加えておきたいと思います。
できる風のビジネスマン、または、できるビジネスマンを目指している学生が、「ロジカルシンキングでイシューをソリューションするために、フレームワークを使って MECE に分解すればよい」とご高説してくれることがあります。ビジネスでよく用いられるフレームワークで、3C 分析や SWOT 分析等といった言葉を聞いた人もいるかもしれません。
このビジネスマンが言うようなフレームワークで考えるというのは、別にビジネスに限ったものではありません。
真面目に高校と大学で勉強していれば、ビジネスに限らずそれぞれの専門分野で色々な枠組みとその適用法を学びます。フレームワーク思考とか言うと、何だかビジネスの世界では特別なことをしており、非常に特殊な技術が必要に思えてしまいます。
しかし、ビジネスで用いるフレームワークは、ただビジネスの分野で使われる「枠組み」であるといった意味でしかありません。
学問を修めて論理的な思考ができれば、ビジネスに限らず、どの分野にも通じる「枠組み」で考えるという当たり前のことを言っているだけです。
枠組み思考・フレームワーク思考は、ビジネスマンになるときに、そこを強調されて教育される傾向があるから、記憶に残りやすいだけです。何も特別なことではありません。というか、ビジネスではない分野でも、真面目に勉強していれば、ビジネスマンの言うフレームワーク思考に対して、「何を当たり前のことを言っているのか? ただお前はビジネスの専門の枠組みを使っているだけだろ」という感想しかでてきません。「枠組みで考える」ことよりも、「枠組み」自体をもっと説明してくれよとなります。
あと、先に言ったご高説は、カタカナばかりですし、大したことは言ってないので、何が言いたいのかよく分からなくてもいいですよ。
こういうのは、必要な人だけが専門語用語的に使えばいいだけですから。使っている人に意味を訊いたら案外答えられない人がいたりします。そもそも、「フレームワーク」なんて言わずに「枠組み」と言う方が、日本語を母語とする我々には理解しやすいです。
また、意味を答えられても、何で日本語で言わないのか理由が不明なことが多いです。和訳せずにカタカナをそのまま使うときは、普通、日本語では抜け落ちてしまうような意味を持たせたり、日常で使っているものとは区別した特別な意味があることを示します。でも、「枠組み」を「フレームワーク」と言う人に訊いても、「フレームワーク」が特殊な意味なのか、日本語では表せない意味を含んだものとして使っているのか、ということに明瞭に答えてくれません。話を聴いていると、それって「枠組み」って言っても何ら問題ないのではないか、と結論づくことが多いです。
何でカタカナ語に対してこんなに物申すのかと言えば、理由があるのですが、長くなりそうなので、また次の機会にとっておきます。
▲雑談に戻る
3.枠組みの問題点
さて、対象を理解するのためには、枠組みを使って、目的達成志向で MECE に分解すればいいことを分かりました。しかし、現実にはあまり上手く行かないことが多いでしょう。現実は非常に複雑であり、相互に絡み合っており、しかも、常に情報が必要十分に揃うとは限らないからです。ですから、文字通り MECE に分解することはほとんどできません。厳密に正確に「ダブりなくモレなく」考えるというのは理想であって、実際にそれが「ダブりなくモレなく」分解できているかを確かめることは非常に難しいです。
特に、商業の世界では、常に利益を追求しておかなければならず、一歩遅れると、競争相手に先を越されたり、機会を逸したりすることになります。一々、枠組みが対象を MECE に分解できているかを確認する時間はありません。ですから、既にある枠組みを使うことが多いです。
したがって、枠組みは完全無欠の完璧なものではなく、枠組みに従って最低限この要素を考えておけば、大きくは外さないといった代物であることに注意が必要です。
一方で、学問や研究者は、細かな違いを検討したり、実際に上手く分類・整理できているかを検証する時間があります。論文等で研究結果を発表し、他の学者から突っ込みを食らうことで、枠組みをより精緻にすることができます。それでも、特に最先端な研究分野では、完全な MECE に分解する枠組みは、中々形成できません。
そして、同じような枠組みを使っているのに、微妙に異なった分類がなされることもあります。
そもそも、枠組みは、複雑な対象を理解するために、考えやすいように境界線を設けたものだと言えます。ですから、細かく見ると、どちらに分類されるか微妙な箇所が出てきます。枠組みは、そうした微妙な箇所を無理矢理単純化して境界線を引いていることが多いです。
説明が少し一般的でしたので、これについて、少し説明したいと思います。
今、ある対象が◇○□の3つの要素群で構成されているとします。
図15.9.枠組みとMECEの概念図
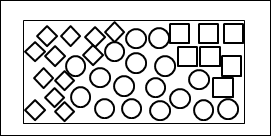
枠組みを設定するということは、対象を理解しやすいように境界線を設定することでした。
したがって、◇の群を A、○の群を B、□の群を C として、群の固まりが分かるように線を引いてやります。
図15.9.枠組みとMECEの概念図
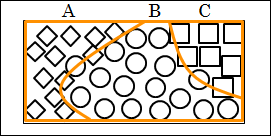
そうすると、一部の○が、 境界線上のど真ん中にあることになります。
その2つの○を分かり易くするため、●と◎とします。
それでは、●と◎の上を境界線が通っていますが、●と◎は、A、B、C のどれに分類すればいいのでしょうか。
境界線上にあるということは、●と◎は「ダブり」があることを意味します。MECE に分類したいので、●と◎も、両方に属すとせずに、どちらかの範疇(カテゴリー)に含めてやる必要があります。
この枠組みでは、●は A に、◎は C に分類することにします。
図15.9.枠組みとMECEの概念図
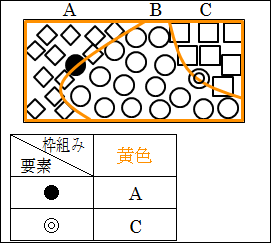
では、このように違う境界線を引いたらどうなるでしょうか。
赤色の破線を引いてみます。
図15.9.枠組みとMECEの概念図
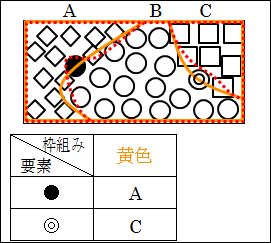
こうすると、●は B に、◎も B に分類されることになります。
図15.9.枠組みとMECEの概念図
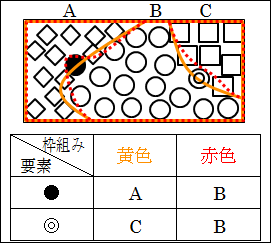
枠組みによって、●と◎は分類される範疇(カテゴリー)が異なることが分かります。
境界線上、または、境界線付近にある要素は、枠組みと考える人によって微妙に分類が変わる場合があるのが理解できます。
実際に、次のような◇○□を細かく分類できる枠組みを設定したとしたら、どうでしょうか。
図15.10.枠組みとMECEの概念図2
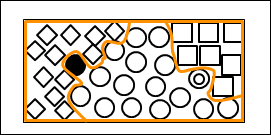
もちろん、このようなきっちり細かく分類できる枠組みをつくってもいいですし、その方が理想的だと言えます。しかし、そうすると、非常に細かい検討をしながら境界線を引かなければなりません。これには、時間も費用も非常にかかります。
速さが重要である商業の世界では、少しくらい例外が出たとしても、対象をある程度正しく理解できれば良しとしてしまうことが多いです。費用と利益を考慮すると、少々乱暴な分析であっても、具体的な作業に取り掛かった方が結果的に良い場合も多いからです。したがって、やや大雑把な枠組み設定を頻繁に用いることになります。
学問や研究の世界でも、やや大雑把な枠組みを用いて対象の研究を進めることもあります。が、境界線上の要素●や◎を詳細に観察して、対象をより正確に理解できるような精密な枠組みをつくったりすることが大切になってきます。学問の目的は、対象をより正確に理解することなので、可能な限り細かい違いが明らかになる枠組みが目指されるからです。おそらく、皆さんも大学で専門を勉強し始めると、こんなんい細かく場合分けしたり、些細な違いに注目する必要があるのか、と思うような知識と出会うことになります。
ちなみに、第 I 部(第10章 論理的思考のまとめ 2 講義の整理)で説明した数ある「推論方法」を「演繹法」か「帰納法」かに分類した時も、厳密に見ると「帰納法」に分類することが微妙である「弁証法」を敢えて「帰納法」に分類しました。
これの枠組みは、「正しい推論を行えば結論が必ず正しくなるかどうか」という基準を設けて「推論方法」を分類しようとしたためです。
つまり、この枠組みは、「論理的思考の最初の段階」であること、「学問的な厳密性よりも実践的な問題解決に使えるような論理的思考の養成」という目的の下でつくられています。そうした目的の下に、ちょっと大雑把な枠組みではあるが、「弁証法」を「帰納法」に分類して「推論方法」という対象を理解しています。
図10.1.推論のまとめ 画像クリックで拡大

このように、適切な枠組みの設定は対象の理解に役立つが、枠組みが完全であるとは限らないっことは常に注意しておかないといけません。
4.基本的な枠組み
では、どのような枠組みがあるのか、という疑問があるでしょう。個々の専門的な枠組みは、学校や大学、あるいは、職場の研修等で学ぶことなので、ここでは個別具体的には触れません。しかし、まったく触れないのも何なので、適用範囲が広く、色々と組み合わせることで、対象を色々な視点から考えることができる枠組みを簡単に紹介しておきます。
| (15.2)基本的な枠組み 時間による枠組み 過去 ― 現在 ― 未来 相違する2軸による枠組み 質 ― 量 ミクロ(個別) ― マクロ(全体) 外的要因 ― 内的要因 対称性・反対概念による枠組み 前(左) ― 後(右) +要因 ― -要因 そのもの ― それ以外 A ― B ― C ― その他 |
ただし、これらの枠組みは、適用範囲が広いため、ある対象のみに狙いを定めて、対象そのものを手っ取り早く、ズバリ理解できるような枠組みではありません。いくつかを組み合わせながら自分で対象を分析する必要があります。この意味については、実際に論理ツリーを作るときに学べます。
他にも、日常に目を向ければ、様々な枠組みが使われていることに気付きます。
例えば、「衣食住」という文句も、「人間が人間らしく生活する上で必要なモノ」を MECE に分解するのを助けてくれています。
文章、主に物語の文章の構成では、「起承転結」という枠組みが有名ですね。
「春夏秋冬」も「季節」を理解するための枠組みと言えます。
また、今まで説明して来た問題解決の過程「課題形成―解決策立案―実行」も、問題を解決する上で必要な要素を MECE に分解していると言えます。
こうした枠組みは、完全かつ正確に対象を理解できるわけではありませんが、外すことができない考慮すべき要素に、MECE に分解していると言えます。
このように、枠組みは、特別で高尚なものではなく、人間が何か考えたりするときに頻繁に使っている地図や基礎的な方針・取っ掛かりだと分かります。
枠組みの設定は、思考を行う上で当たり前のことだとなので、それを使いこなせるようになるためにも、自分なりに色々な枠組みを様々な対象に当てはめて考えてみてください。そして、ある対象を理解するのに適した枠組みが見つけられると、対象が一体何なのかという本質が理解できていることに気付くはずです。
これを逆に利用すれば、どの枠組みを適用すればよいかを知りたいとき、対象の本質とは一体何なのかを考えてみると良いと言えます。
枠組みを設定することで、対象を本質的に理解できる。これは、今まで枠組みの役割として説明し来たことです。
図15.11.枠組みの設定方法

どの枠組みが適切なのかが分からないとき、これを逆手にとって、対象の本質とは何かを考えて、その本質を焙り出せるような枠組みを設定します。
図15.11.枠組みの設定方法
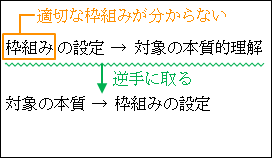
このとき、気を付けてもらいたいことがあります。
通常の場合は、枠組みを設定して対象を本質的に理解できるという順番です。これと逆の手順をしているので、対象が本質的に理解できたのかを確認しないといけません。「逆は必ずしも真ならず」です。
図15.11.枠組みの設定方法
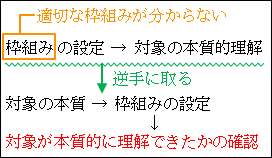
もし対象が本質的に理解できていたら、枠組みが正しかったと分かります。
もし対象が本質的に理解できていなかったら、枠組みが正しくなかったと分かります。その場合は、改めて対象の本質を考え直して、違う枠組みを設定してみます。
このように、対象の本質を考えることで、適用すべき枠組みが絞られていくはずです。
5.枠組みを自分でつくる
枠組みが対象を考える上で非常に役に立つことを力説してきたわけですが、巷では、枠組み思考が批判されているのを聞いたことがある人もいるでしょう。「既存の考え方では、問題は解決できない。新しい創造的な発想が必要だ。柔軟な思考ができなければならない」といった批判です。大学入試もこの流れで暗記偏重でダメだと批判されているのは、一度は見聞きしたことがあるはずです。
実際のところ、斬新で柔軟な発想が何を指しているのか分からないので、深くは突っ込みませんが、既に在る枠組みを使うだけでは足りないという主張自体は、正しいと言えます。
今、情報化社会で、もの凄い速さで問題が増えて行きます。そこでは、今までのやり方を単に当てはめるだけでは上手く解決できないような問題が増えて来ています。しかも、問題がどんどん出て来るので、1つ1つに時間をかけることも難しくなっています。それゆえに、既存の枠組みに囚われずに、自分で解決策を考えなければならないことが、とんでもない速度で増えていることになります。そして、既存の枠組みは、学校の勉強等で知識として仕入れることになっています。
このことから、暗記偏重ではダメだという言説が叫ばれるようになっていると判断できます。そして、知識に頼る部分が大きい既存の枠組みを適用して考えるのではなく、自分の頭で考えて新しい枠組みをつくることが求められているということになります。
前置きが長くなりましたが、要は、既存の枠組みで考えるのではなく、1から自分の頭で考えることが大切であるということです。したがって、対象の本質を捉えるための枠組みも、1から自分で組み立てていくことが必要になります。
自分で枠組みを作らなければならないとき、強力で応用性が高い枠組みが、「そのもの」と「それ以外」で分ける枠組みです。
もちろん、「そのもの」と「それ以外」で分ける枠組みが、毎回毎回上手いくわけではありませんが、上手くいく確率は非常に高いです。なぜならば、「そのもの」と「それ以外」で分ける枠組みは、初歩的で基礎的ではあるが、まさに基礎的だからこそ、多くの事柄の土台となり得るからです。
先程見た「推論方法」の分類でも、「そのもの」と「それ以外」という枠組みを使っていました。
改めて、「推論方法」を「演繹法」、「枚挙的帰納法」、「仮説推論」、「類比推論」、「弁証法」の5つに分類して、「そのもの」と「それ以外」の枠組みの使い方に慣れたいと思います。
| (15.3)演繹法、枚挙的帰納法、仮説推論、類比推論、弁証法の5つの推論方法を「そのもの」と「それ以外」で分ける枠組みを使って分類せよ |
使う枠組みが、「そのもの」か「それ以外」かで分類するものを使うとは言え、何について分けるかが未だ具体的ではありません。そこで、枠組みを設定するために、考える対象である「推論方法」の本質について考えることにします。
では先ず、「推論方法」とは何でしょうか。
「推論」とは「既知のコトから未知のコトを論理的に導くこと」でした(第 I 部 第1章 論理的であるとは 3 推論とその問題点)。したがって、「推論方法」は、「既知のコトから未知のコトを論理的に導く方法」ということになります。
| (15.3)演繹法、枚挙的帰納法、仮説推論、類比推論、弁証法の5つの推論方法を「そのもの」と「それ以外」で分ける枠組みを使って分類せよ 対象の本質を考える
|
そして、既に知っているコトから、未だ知らないコトを考え出すことができるので、何かを考えるとき「推論」が強力な武器になるわけでした。それゆえに、「論理的に導かれた結論」が「正しい」ことが推論を用いる大きな理由でした。
これを踏まえて、「推論方法」を分類するとき、「正しい推論による結論がどうなるか」という基準が重要になります。
| (15.3)演繹法、枚挙的帰納法、仮説推論、類比推論、弁証法の5つの推論方法を「そのもの」と「それ以外」で分ける枠組みを使って分類せよ 対象の本質を考える
→枠組みの設定
|
それでは、「正しい推論による結論がどうなるか」という基準から「推論方法」を分類していきます。
「正しい推論による結論」が、「必ず正しい」か「必ず正しいとは限らない」かという枠組みを使います。
「必ず正しい」が、「そのもの」=「A である」という範疇(カテゴリー)です。
「必ず正しいとは限らない」が、「それ以外」=「A ではない」という範疇(カテゴリー)です。
図15.12.推論の分類(図10.2.の再製) 画像クリックで拡大
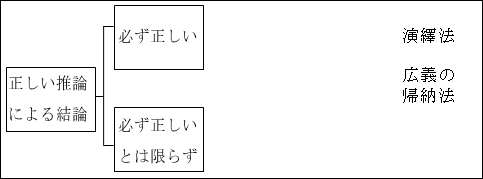
なお、「必ず正しい」の否定は、「必ず正しくない」ではありません。これでは、100%絶対に正しいことが有り得ないことになってしまいます。
「必ず」は、「すべての場合」と読み換えることができるので、「すべて」の否定は、部分否定と考えないといけません(第 I 部 第2章 推論方法の基礎 3 全称と特称)。ですから、「必ず正しい」を部分否定して、「必ず正しいとは限らない」としなければなりません。
さて、推論方法の中で、「必ず正しい」結論になる推論は、「演繹法」の1つだけでした。
そして、「演繹法」以外の推論方法は、「必ず正しいとは限らない」ものであると分かります。これが広義の帰納法と呼ばれる推論方法でした。
しかしながら、「演繹法」とそれ以外の4つの推論方法という分け方では、それ以外の4つの推論方法の違いがよく分かりません。
そこで、「必ず正しいとは限らない」推論方法をさらに分けます。
まず確認ですが、「必ず正しいとは限らない」ということの意味は、「正しい」場合もあれば、「正しくない」場合もある、ということです。
したがって、どの程度の確率で「正しい」のかという基準が重要になります。
| 必ず正しいとは限らない =正しい場合もあれば正しくない場合もある →基準:どの程度の確率で正しいのか |
そこで、新たに「仮説性が弱い」か「仮説性が強い」かという枠組みで分類します。
なお、「仮説」とは「事実に対する仮の説明」です。したがって、「仮説性」は「事実に対する仮の説明である傾向」という意味になります。
「仮の説明である傾向」が弱ければ弱いほど、それは事実そのものを説明していると言えます。
逆に、「仮の説明である傾向」が強ければ強いほど、それは事実そのものを説明しているか分からない、まさに「仮の説明」である確率が強くなります。
ただし、「仮説性が弱い」という表現はあまり一般的ではありませんが、ここでは「強い」ことと対比するために、「弱い」という表現を使っています。
「仮説性が弱い」か「仮説性が強い」かの枠組みも、「そのもの」と「それ以外」が応用されています。
「仮説性が弱い」が、「そのもの」=「A である」という範疇(カテゴリー)です。
「仮説性が強い」が、「それ以外」=「A ではない」という範疇(カテゴリー)です。
ただし、厳密に「弱い」ことを否定すると、「普通」と「強い」が含まれるように「弱くはない」とするべきところですが、物事を単純化して考えやすくするために、「弱い」か「強い」かの2つにザックリと分けています。
| 必ず正しいとは限らない =正しい場合もあれば正しくない場合もある →基準:どの程度の確率で正しいのか →枠組みの設定
|
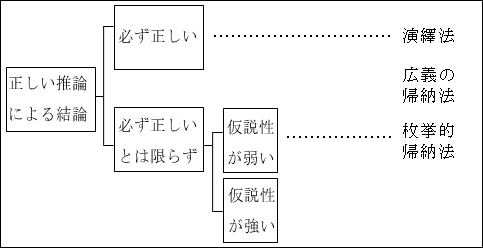
「必ず正しいとは限らない」が「仮説性が弱い」である推論方法には、「枚挙的帰納法」が当てはまりました。
似たような観察事実を積み重ねて、事実を寄せ集めるように、一般的な命題を推論するため、仮説性が弱く、つまり、正しい確率が必然的に高くなります。しかし、すべての場合を調べることが難しいので、「必ず正しい」とも言えなかったのでした。
そして、それ以外の「仮説推論」、「類比推論」、「弁証法」は、「必ず正しいとは限らない」上に、「仮説性が強い」推論方法となります。
図15.12.推論の分類(図10.2.の再製) 画像クリックで拡大
さらに、「仮説推論」、「類比推論」、「弁証法」を分類しましょう。
ここからは、推論それ自体の特徴よりも、人間の思考様式に関わってきます。「推論方法」について細かく考えていっているので、どんどん抽象的な様式から具体的な作法になっていきます。
人間は物を考えるとき、ある観念を他の観念に結びつけながら思考します。これを観念連合と言いました。
そして、観念を結びつけるとき、物事の特徴を比較します。物事を比較するとき、「類似性」に注目するか否かが重要になります。
無論、考えているときにまったく「類似性」を考慮しないという状況は想定しづらく、多かれ少なかれ「類似性」を手掛かりに思考しているものです。しかし、ここでは、特に「類似性」に重きを置いて推論する、言い換えるならば、「類似性」を柱として中心に推論しているという意味で、「類似性」に注目すると述べています。
そこで、「類似性に注目しない」か「類似性に注目する」かという枠組みで分類します。
これも、「そのもの」と「それ以外」という枠組みが用いられています。
「類似性に注目する」が、「そのもの」=「A である」という範疇(カテゴリー)です。
「類似性に注目しない」が、「それ以外」=「A ではない」という範疇(カテゴリー)です。
ただし、「推論方法」の性質上、「類似性」に特に注目しないことの方が一般的なので、論理ツリーにおいける範疇(カテゴリー)の並べ方は、「類似性に注目しない」を上に、「類似性に注目する」を下に配置しています。
| 人間は観念と観念を結びつける観念連合で考える =物事の特徴の比較 →基準:類似性に注目するかどうか →枠組みの設定
|
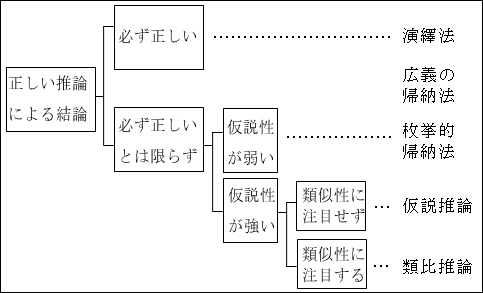
「必ず正しいとは限らない」かつ「仮説性が強い」もので、「類似性に注目しない」推論方法が「仮説推論」となります。
「類似性に注目する」推論方法が、「類比推論」となります。
図15.12.推論の分類(図10.2.の再製) 画像クリックで拡大
ここで困ったことがあります。「弁証法」がどこにも分類されません。
「弁証法」は、正―反―合の流れによる推論ですが、これは「類似性」に特に注目しているわけではありません。ですから、「仮説推論」と同様に、「類似性に注目しない」という範疇(カテゴリー)に含めても良い気がします。が、「仮説推論」と「弁証法」はあまりにも性質が違うので、どうもスッキリしません。
仕方がないので、「その他」という範疇(カテゴリー)をつくって、「弁証法」をそこに分類してやります。
これは「そのもの」と「それ以外」の枠組みを拡張しています。先程、「類似性に注目する」か「類似性に注目しない」かの枠組みを作りましたが、この枠組みに収まらないものを「その他」の範疇(カテゴリー)に詰め込むという具合です。
つまり、まず、「そのもの」と「それ以外」で枠組みを作ります。
次に、その枠組みでは収まらないものを「その他」としています。
なお、これは、「A ― B ― C ― その他」の枠組みとも言えます。ただ、いきなり「A」「B」「その他」という枠組みを作ろうとしてもMECEに上手く分解できるものではありません。ですから、「そのもの」と「それ以外」で分解してから、余ったものを「その他」に入れるという手順を踏んでいます。
|
「類似性に注目しない」と「類似性に注目する」と「その他」という範疇(カテゴリー)を設けます。
そして、「その他」の範疇(カテゴリー)に、「弁証法」を分類します。
図15.12.推論の分類(図10.2.の再製) 画像クリックで拡大

こうして、「そのもの」と「それ以外」の枠組みを応用しながら、「推論方法」について分類しました。
哲学や論理学の専門的な知識を使わずに、各推論の本質を考えながら、1から自分で考えながら、適切に枠組みを設定して分類していきました。もちろん、各推論がどういった特徴を持っているのかは知らないと始まりませんが、少なくとも「推論方法の分類」に関する専門的な知識は使っていません。
「そのもの」と「それ以外」で分ける枠組みの強力さと応用性が分かったかと思います。また、1から自分で考えることも分かったかと思います。
なお、他にも色々な分類方法があります。
そもそも、「弁証法」が「演繹法」や「広義の帰納法」とは毛色が違うということをもっと前面に押し出したいのならば、「その他」の範疇(カテゴリー)を、もっと高次の第2階層に持って来ることもできます。
「演繹法」や「広義の帰納法」が結論を論理的に推論することに焦点が置かれているのに対して、「弁証法」は論理性を重視しながらも、世界を統一的に理解しようという精神的な活動の面が強かったからでした。
図15.13.推論の分類2 画像クリックで拡大
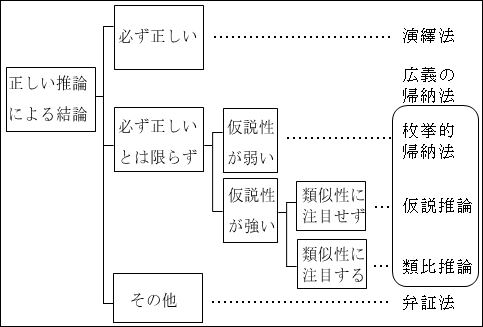
これから分かる通り、「弁証法」をどうやって分類するかは、考える人によって微妙に異なります。
こうした分類の仕方に微妙な違いがることに気付けたのも、1から枠組みで考えて行くときに、どの範疇(カテゴリー)にも当てはまらないモノが存在することに気付けたからです。
こうした理由で、哲学や論理学では、「演繹法」と「広義の帰納法」という大きな2本柱があり、そこに少し毛色が違う「弁証法」が存在している、という分類がなされることが多いです。
「演繹法」と「広義の帰納法」と同格にして抽象度の次元を合せるために、「弁証法」を「広義の帰納法」に含めるよりも独立して扱い、「弁証法」の範疇(カテゴリー)を、第2階層に持って来た枠組みを設定します。
第 I 部では、大枠が理解できるように、「弁証法」を「広義の帰納法」に分類しましたが、ここまで学んだ人にとっては「弁証法」を「広義の帰納法」から独立させて考えることにも抵抗なく受け入れられるはずです。
なお、これも、同じ様な枠組みを使っても、人によって分類方法に微妙な違いが出て来る例の1つです。
以上のように、「そのもの」と「それ以外」という枠組みは、自分で対象の本質を考えることで、自分なりに枠組みを構成することの第一歩になることが分かりました。特別な枠組みを知らない場合でも、自分で考えるのに強力で応用力のある枠組みなのです。
そして、既存の枠組みが使えない場合は、このように自分で枠組みをつくってみてください。一発で妥当な枠組みをつくれることは滅多にないので、試行錯誤しながら、納得のいくように作ってみてください。これが考えることの練習です。
また、既存の枠組みでも、ただ用いるだけでなく、何故このような枠組みを使うのか、どうやってこの枠組みは作られたのかということを、一度自分なりに「そのもの」と「それ以外」という枠組み等から考えてみるといいです。そうすることで、枠組みの適用の仕方や対象の理解が一層進みます。
6.合理的な前提条件
また、枠組みを使って論理ツリーをつくるときには、合理的な前提条件を明確に設定しておく必要があります。なお、「合理的な」とは、「目的に合った」という意味です。「推論方法」を分類するときにも、「推論を、その形式に応じて、分類する」という前提条件がありました。
「推論方法」を分類するという目的を達成する上で、「推論の形式」に着目するという前提が置かれています。こうした前提が置かれることで、思考が際限なく発散することを防ぎます。
こうした目的に合った前提条件を設定しておくことが大切です。
今回の例は、前提条件を置かなくても、そんなに問題になりませんが、問題解決の実践時には、前提条件を上手く置いておくことが必要になります。
当たり前のことですが、問題解決の実践時には、現実の状態を規定する様々な条件があります。典型的には、制約条件がこれにあたります。予算の制約や場所の制約、人材の制約といったことは予め動かすことのできない前提条件です。それ以外にも、問題が起きている状況によっては、昼の出来事として限定するといったこと等も前提条件になります。要は、こうした前提条件を無視すると、問題解決と無関係のことも際限なく考えることになり、結論を得るのに、とでもない時間がかかります。最悪の場合、結論に到達する前に時間切れになったり、考えが広がり過ぎた結果、妥当ではない結論に行く着くことも有り得ます。
したがって、前提条件を上手く置いて考えることが大切です。次の章以降で、事例に即して確認します。
もちろん、前提条件のすべてが、最初から明確になっているわけではありません。
考えて行く過程で、思考が発散します。「あーでもない、こーでもない」と色々と考えます。そして、考慮しなければならない前提条件が見つかり、収束していくものです。
その場合は、論理ツリーそのものに書き込むことがなくとも、欄外に前提条件「~」と記しておくといいです。行き詰まった際にでも、前提条件を確認して、無駄に思考が拡散するのを防ぐことができます。
7.上位と下位の階層関係
論理ツリーを枠組みを使って作ったときに、上位階層と下位階層ができました。この上位階層と下位階層の関係について検討します。論理ツリーの上位階層と下位階層の関係をよく見ると、上位階層の範疇(カテゴリー)は、下位階層の範疇(カテゴリー)を縛っていることが分かります。
図15.12.推論の分類(図10.2.の再製) 画像クリックで拡大

第2階層には「必ず正しいとは限らない」という命題があり、第3階層には「仮説性が弱い」という命題があります。
このことが意味することは、推論方法の中で、「必ず正しいとは限らない」推論があり、さらにその中で「仮説性が弱い」推論だということです。
集合図で表すと、このように描けます。
図15.14.上位―下位階層の関係
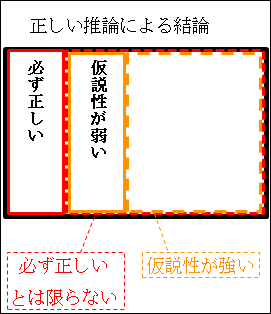
1番外側の黒色の枠の四角形が、「推論方法」全体を表しています。
その中の赤色の破線の枠の四角形が、「必ず正しいとは限らない」推論方法を表しています。
さらにその中の黄色の枠の四角形が、「仮説性が弱い」推論方法を表しています。
黄色の枠の四角形である「仮説性が弱い」を考えると、赤色の破線の中に存在するので、自動的に「必ず正しいとは限らない」という要素も含んだものになることが分かります。
このことから、下位階層の範疇(カテゴリー)は、自動的に上位階層の範疇(カテゴリー)が持つ特徴に縛られるのが分かります。
ですから、ある階層の命題については、上位階層から各範疇(カテゴリー)を順に拾って、適切な接続詞で結んでやれば、その定義や意味を明確にできます。
例えば、「『枚挙的帰納法』とは何なのか?」と考えたとき、上から順に範疇(カテゴリー)を拾って接続詞を補うとこのようになります。
まず、論理ツリーを見ただけで、「必ず正しいとは限らない」推論で「仮説性が弱い」推論が、「枚挙的帰納法」だと理解することができます。
これを通りの良い文にするために、適切な接続詞で補ってやると、「枚挙的帰納法」とは、「正しい推論によって導かれる結論」が「必ず正しいとは限らない」が、「仮説性が弱い」推論方法である、と分かります。
ちなみに、先にまとめた「推論方法」の論理ツリーを集合図で描くとこのようになります。論理ツリーと照らしてみて、理解を深めて置いてください。
図15.15.上位―下位階層の関係1
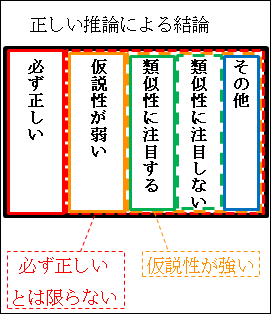
図15.16.上位―下位階層の関係2 画像クリックで拡大
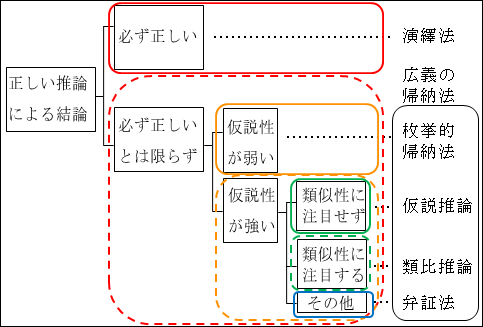
このことから同時に、下位階層の範疇(カテゴリー)は、上位階層の範疇(カテゴリー)を前提として、考えなければならないことが分かります。
もし、上位階層の範疇(カテゴリー)からはみ出したり、収まらないような範疇(カテゴリー)になったら、それは枠組みが不適切である可能性が高いです。
例えば、「仮説性が強い」という上位階層の範疇(カテゴリー)の下に置かれているにもかかわらず、「必ず正しい」という範疇(カテゴリー)が出て来るのはおかしいということになります。「仮説性が強い」時点で、「必ず正しい」と言うことができないからです。ですから、上位階層の範疇(カテゴリー)の制限の中で、下位階層の範疇(カテゴリー)を考える必要があります。
そして、上位階層の範疇(カテゴリー)から、はみ出したり矛盾するよう下位階層の範疇(カテゴリー)が出てしまったときは、より適切な枠組みを考えるべきだということの示唆なので、枠組みを洗練する良い機会と捉えて、より対象の本質に迫った分類を考えます。
この上位階層と下位階層の関係は、次章の why ツリーの作成でも詳しく触れることにします。
4 適切な枠組み設定
枠組みを設定することで、対象を理解できるようにMECEに分解できることが分かったかと思います。そこで、適切な枠組みをどう設定すべきか、ということについてもう少し深く考えてみます。
枠組みは、対象の本質を考えながら適切に設定していったわけですが、本質を考える上で、どのようなことに気を付けなければならないのでしょうか。
1.上位階層 ― 一般的・抽象的な枠組み
まず、上位階層には適度に高い一般的・抽象的な枠組みを設定することが大切です。
「推論方法」の分類のために枠組みを設定するとき、最初に、「正しい推論による結論」が「必ず正しい」か「必ず正しいとは限らない」かという枠組みを設定しました。この枠組みはかなり抽象度の高いものだと分かるでしょうか。このことについて見て行きましょう。
もし、最初に「正しい推論による結論」について、「仮説性が弱い」か「仮説性が強い」かという枠組みを使ったとしたら、どうなるでしょうか。
図15.17.推論方法の分類3-1 画像クリックで拡大 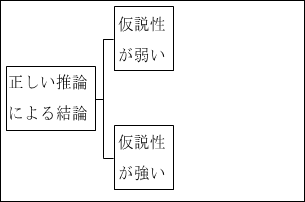
図15.12では、「仮説性が弱い」推論には、「枚挙的帰納法」のみが分類されていました。
「仮説性が強い」推論には、「仮説推論」「類比推論」「弁証法」が分類されていました。
図15.12.推論の分類(図10.2.の再製) 画像クリックで拡大 
これに従うと、最初に「仮説性が弱い」か「仮説性が強い」かの枠組みを当てはめた場合、「演繹法」がどこにも当てはまらないことになります。
このままでは、演繹法がどこの範疇(カテゴリー)にも入らず、「モレ」のある分類になってしまいます。
図15.17.推論方法の分類3-1 画像クリックで拡大 
しかし、「演繹法」は「正しい推論によって導かれた結論」が「必ず正しい」ことになる推論という点を考えると、「仮説性が弱い」推論に分類することも一応はできます。
図15.18.推論方法の分類3-2 画像クリックで拡大 
そうすると、「演繹法」と「枚挙的帰納法」が、ある種の近い推論方法であると捉えることができます。
そして、同時に、他の3つの推論である「仮説推論」「類比推論」「弁証法」と明確に区別されます。
つまり、推論は大別すると2種類あり、「仮説性が弱い」推論と「仮説性が強い」推論がある。すなわち、推論として正しい確率が高いものに「演繹法」と「枚挙的帰納法」があり、推論として正しい確率が高くないものに「仮説推論」「類比推論」「弁証法」がある、ということになります。
図15.18.推論方法の分類3-2 画像クリックで拡大 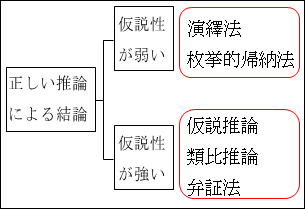
そして、このとき、「広義の帰納法」という理解は崩れ去るります。
図15.18.推論方法の分類3-2 画像クリックで拡大 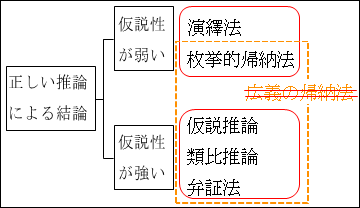
図15.12(あるいは図15.16)では、「広義の帰納法」は、辿って行くと第2階層に行きつくように分類されていました。
ですから、第2階層の「必ず正しいとは限らない」に分類される推論方法をまとめて「広義の帰納法」とできました。
図15.16.上位―下位階層の関係2 画像クリックで拡大 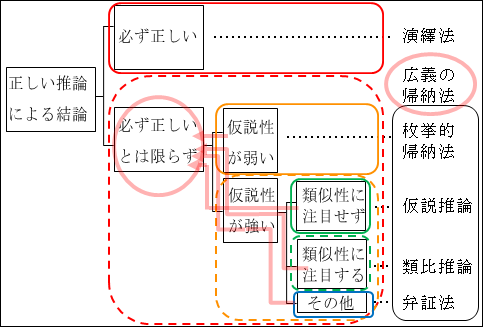
しかし、図15.18では、「枚挙的帰納法」と「仮説推論」「類比推論」「弁証法」は第2階層まで戻ったときに、異なる範疇(カテゴリー)に分類されています。
両者が出会う範疇(カテゴリー)まで遡ると、「正しい推論に導かれる結論」の最上位階層(トップボックス)まで行き着くので、「推論方法」という大きな枠でしかまとめられません。
図15.18.推論方法の分類3-2 画像クリックで拡大 
そして、もし、図15.12(あるいは図15.16)と同じように「広義の帰納法」でまとめると、異なる範疇(カテゴリー)にまたがることになります。
つまり、異なる範疇(カテゴリー)にまたがるのにもかかわらず、仮に「広義の帰納法」とまとめてしまうと、「ダブりのある」分解をしているということになります。
「広義の帰納法」について、「仮説性が強い」という範疇(カテゴリー)を中心に考えるとしましょう。
このとき、「枚挙的帰納法」は「仮説性が弱い」という範疇(カテゴリー)に分類されているにもかかわらず、「仮説性が強い」という範疇(カテゴリー)にある「広義の帰納法」にも分類されてしまっていることになります。
逆に、「広義の帰納法」について、「仮説性が弱い」という範疇を中心に考えるとしましょう。
「仮説推論」「類比推論」「弁証法」は「仮説性が強い」という範疇(カテゴリー)に分類されているにもかかわらず、「仮説性が弱い」という範疇(カテゴリー)にある「広義の帰納法」にも分類されてしまいます。
いずれにしろ、「ダブり」が生じた分類になっています。
このことから、最初に「仮説性が弱い」か「仮説性が強い」かの枠組みでは、「広義の帰納法」という理解は MECE に反することになります。
しかし、「必ず正しいか否か」という基準で分けた後に、「仮説性の強弱」という基準で分けた場合(図15.12あるいは図15.16)では、「広義の帰納法」という概念が崩れることなく「推論方法」を分類できました。何故なのでしょうか。
その理由は、「必ず正しいか否か」という基準は、「仮説性の強弱」よりも抽象度が高い枠組みだからです。
つまり、抽象度で見ると、「必ず正しいか否か」は、「仮説性の強弱」よりも抽象度が高いのです。
「必ず正しい」か「必ず正しいとは限らない」かという枠組みは、結論が正しい確率に関わってきます。この枠組み全体で、確率として、0~100%を網羅しています。
図15.19.推論が正しい確率 
「必ず正しい」は、ずばり100%のみを表します。
「必ず正しいとは限らない」は、0~99.999…%と幅があります。
図15.19.推論が正しい確率 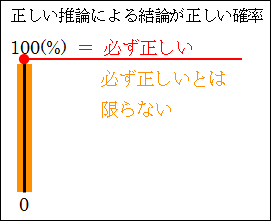
そして、「仮説性」の強弱も、結論が正しい確率の高低に関わっています。
つまり、「仮説性が弱い」か「仮説性が強い」かという枠組みも、確率として0~100%全体を表すと言えそうです。
が、しかし、「仮説性」という言葉の意味を今一度よく考えてみてください。
「仮説性」は、「事実を正しく説明している可能性の度合い」という意味です。
100%正しい、つまり、「必ず正しい」場合というのは、「仮説」とは呼ぶよりは「事実」や「定理」と呼んだ方が適切になります。
つまり、「仮説性」を問題にしている時点で、100%必ず正しいものは除外されます。そして、「仮説性」が問題としているのは、0~99.999…%の間のどこなのか、ということになります。
図15.19.推論が正しい確率 
このように、言葉の意味を細かく考えてみると、「仮説性の強弱」は、「必ず正しい」か「必ず正しいとは限らない」かの枠組みの中の「必ず正しいとは限らない」の範疇(カテゴリー)に含まれることが分かります。
したがって、「必ず正しいか否か」という枠組みの方が網羅している範囲が広く、「仮説性の強弱」はその中の全体ではなく一部を網羅していることになります。
つまり、「必ず正しいか否か」の方が、「仮説性の強弱」よりも抽象度が高い、あるいは、より一般的である、と言えます。
そもそも、論理ツリーとは、抽象度の高い命題や概念に対して、MECE に分解して具体的な要素にして行くための道具です。
このことを考えれば、枠組みを適用する順番は、抽象度の高いものから順に適用していくのが基本となるのも理に適っています。
ですから、「必ず正しいか否か」よりも抽象度が低い「仮説性の強弱」という枠組みを最初に適用すると、各推論方法が持つ特徴が曖昧になってしまい、「ダブりなくモレなく」分解できないという結果を招くことになります。
このように、上位階層ほど抽象度が高くなるように枠組みを設定していくことが大切になります。
ただし、「仮説性の強弱」の枠組みから、「必ず正しいか否か」の枠組みを設定するのも目的によっては、アリの場合もあります。
それは、目的が「推論方法を分類する」のは同じですが、予め「演繹法」と「帰納法」の2つが理解できており、それに加えて新しい推論方法を学ぶ場合です。
この講義で初めて「演繹法」と「帰納法」という考え方があると知った人以外は、推論方法や思考法として「演繹法」と「帰納法」という2つの柱があることを、高校の授業、または何かしらで習った経験があるはずです。それだけ「演繹法」も「帰納法」も超有名な推論方法です。
しかし、「仮説推論」や「類比推論」といった考え方は、「演繹法」や「帰納法」に比べてあまり有名ではありません。もちろん、説明されれば、当たり前の考え方に思えますが、初めて「仮説推論」や「類比推論」を学ぶときには、「演繹法」と「帰納法」との相違点を浮かび上がらせた方が理解しやすいはずです。
まず、「仮説性の弱い」推論として、「演繹法」と「帰納法」を分類します。
「仮説性が弱い」推論の中でも、「必ず正しい」推論が、「演繹法」となります。
「仮説性が弱い」推論の中でも、「必ず正しいとは限らない」推論が、「枚挙的帰納法」となります。
なお、ここでの「枚挙的帰納法」は、単純に「帰納法」と呼んでも一向に構いません。「広義の帰納法」という枠組みがなくなったので、単に「帰納法」としても混乱しないからです。
図15.20.推論方法の分類4 画像クリックで拡大 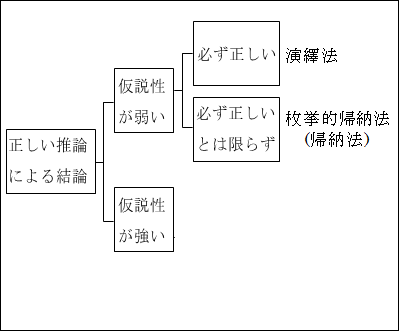
そして、「仮説性の弱い」推論が、「演繹法」と「帰納法」であるとすると、それと対比して、そうではない推論である「仮説性の強い」推論という特殊性が強調されます。
つまり、
世の中には、「演繹法」や「帰納法」という「仮説性が弱い」推論方法がある。それで導かれる結論は正しい確率が100%か、それに近いくらいにかなり高い。
しかし、世の中には、「演繹法」でも「帰納法」でもなく、範疇(カテゴリー)を異にする推論方法がある。それで導かれる結論は正しい確率が必ずしも高くない。
ということが対比的に表すことで明確に示せます。
後は、「仮説性の強い」推論に対して、「類似性に注目しない」か「類似性に注目する」かという枠組みを当てはめれば、「仮説推論」と「類比推論」という推論方法が存在していることを明らかにできます。
図15.20.推論方法の分類4 画像クリックで拡大 
こうすることで、「演繹法」と「帰納法」しかないと思っていた人に対しては、他にも推論方法があることを強調して説明できます。
つまり、「枚挙的帰納法」「仮説推論」「類比推論」を「広義の帰納法」として説明する(図15.12あるいは図15.16)より、
「演繹法」と「(枚挙的)帰納法」とは区別して、その他に「仮説推論」や「類比推論」といった推論方法があることを前面に押し出して説明できます(図15.20)。
「演繹法」と「(枚挙的)帰納法」は、導かれる結論の正しい確率がかなり高い推論方法です。ですから、中学や高校のような勉強の初歩の段階で、「演繹法」と「(枚挙的)帰納法」が教えられることが多いわけです。
これに対して、「仮説推論」や「類比推論」は、導かれる結論の正しい確率があまり高いとは言えない推論方法です。ですが、学問を始めとして色々な分野で、この推論方法なしに世の中は回らない、必要不可欠な推論方法でもあります。
そこで、勉強がある程度進んだら、「仮説推論」や「類比推論」を、「演繹法」や「(枚挙的)帰納法」に追加して学ぶことになります。そして、「演繹法」や「(枚挙的)帰納法」ではあまり言われなかった仮説を検証することの重要性等が説かれます。
図15.20.推論方法の分類4 画像クリックで拡大 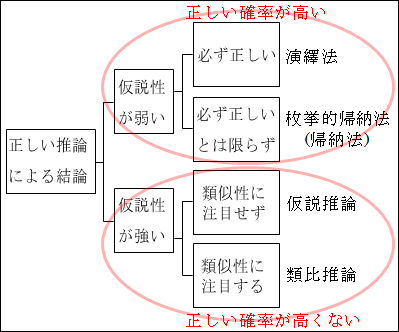
このように、最初に「演繹法」と「(枚挙的)帰納法」についての知識が確固として存在しているなら、「仮説推論」と「類比推論」を勉強する際には、「演繹法」と「(枚挙的)帰納法」とは異なる範疇(カテゴリー)にある推論方法として対比させることで、相違点が明確になり理解が進みます。
既に記憶されている「演繹法」と「(枚挙的)帰納法」という大きな枠に、「仮説推論」と「類比推論」という異なる大きな枠を対比させながら結びつけているため、理解がしやすいわけです。これも観念連合の一種です。
以上のように、抽象度が高い順に枠組みを設定していくという原則に反しても、既存の知識を活かして対象を上手く相手に理解させるにはどうすればよいかという目的の下では、効果的になる場合もあるのが分かったでしょうか。
もう少し正確に言えば、対象をどう理解するのかという目的に応じて、枠組みの抽象度や一般性の度合いは変わる、と言えます。枠組みの抽象度も一般性も相対的なものだと分かります。
また、枠組みが適切か否かは目的によって変わることの例の1つです。
そして、物事を色々な角度から考えることで、対象の理解が進むことの例でもあります。
しかしながら、ここまで説明しておいて何ですが、よくよく考えて推論方法を整理すると、「仮説推論」も「類比推論」も「広義の帰納法」に分類した方が、各推論の特徴を捉えた一般的で普遍的な理解に適していることはよく分かるかと思います(図15.12あるいは図15.16)。
ですから、「演繹法」と「帰納法」のみを知っている人に対して、「仮説推論」や「類比推論」の存在を説明できたら、改めて「必ず正しい」か「必ず正しいとは限らない」かの枠組みから組み立てた論理ツリーを使って整理し直した形で示せばいいでしょう。
2.対象の本質と枠組みの必然性
さて、上位階層に適度に高い一般的・抽象的な枠組みを設定することに加えて、枠組みを設定する際には、対象の本質と枠組みの必然性を考えることが大切です。
これは、図15.11.枠組みの設定方法(3 枠組み 4.基本的な枠組み)のところで説明したことと共通します。
どの枠組みを設定すればいいのか分からないとき、対象の本質とは一体何なのかを考えると、手掛かりが見つかることがあると説明しました。
改めて、対象の本質から必然的な枠組みを考えることを軽く確認しておきましょう。
| (15.4)「推論方法」を分類し整理するとき、最初に「類似性に注目するか否か」という基準ではなく、「必ず正しいか否か」という基準で考え始めた理由はなぜか |
「推論方法」を理解しようとするとき、そもそも「推論」とは何なのか、なぜ推論をするのかといったことを考えていました。
「推論」とは、「既知のコトから未知のコトを論理的に導くこと」でした。したがって、「推論」の性質を考える上で、「未知のコト」について論理的に導かれた結論が、事実と合致していることが重要です。それゆえに、「どれだけ正しい確率が高いのか」といった観点から枠組みが設定されました。
もし、「方法」に注目すれば、 いきなり「類似性に注目しない」か「類似性に注目する」かという枠組みを当てはめることになるでしょう。
しかし、上位階層でこのような枠組みを設定するのは、あまりよくありません。
このことについて少し詳しく見てみましょう。
そもそも、人間の思考の特性上、多かれ少なかれ物事の「類似性」に注目して色々と考えるものです。
何かと何かを比べて類似点や対比点に気付くのは、確かに人間の思考上は本質的と言えます。
図15.21.思考の特性
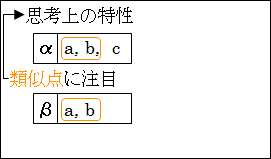
推論も、その例に漏れません。
すべての推論は何かしらの「類似性」を手掛かりにしていると言ってもいいくらいです。そう考えると、「類似性」に注目して、「推論方法」を分析するのは本質的である気もします。
図15.21.思考の特性
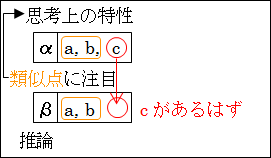
ですが、「類似性」はどの推論にも使われているがゆえに、 「類似性」によって分類することが非常に難しくなります。
比較による気付きは、人間が物を考えるときにほぼ自動的に使ってしまう方法であり、それゆえに、単なる勘違いの可能性も捨てきれないのも事実なのです。ですから、類似点から何かを予測するとき、必ずしも正しいとは限らず、間違えて誤った結論 を導いてしまうことも多いのです。悲しいことかな、人間の思考上の特性とは、誤りやすいものなのです。
図15.21.思考の特性
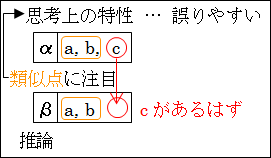
そうしたことを踏まえた上で、可能な限り未知の事柄を正しく見通したいから、「推論方法」について考えているのが始まりでした。
「類似性」に否が応でも反応してしまい、それに引っ張られるという人間の思考上の特性から、少し冷静になって距離を置きたいわけです。そして、正しく未知の事柄を導くために、様々な「推論方法」を考え出しているのです。
まとめると、「推論方法」について考えている理由は、「推論」によって導かれる結論が正しくなる確率を上げるためにはどうすればいいのか、という方法を考えているためです。
図15.21.思考の特性
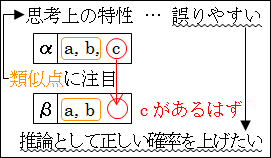
こうした事情から、「推論方法」の本質として、「類似点に注目するか否か」という枠組みを抽象的な段階である上位階層に当てはめるのは、あまり必然的とは言えないことが分かります。
「類似性」に注目してしまうという思考上の特性から離れて考えることができないからです。
これが、「人間の思考上の特性の本質」を考えているのなら、「類似点に注目するか否か」という枠組みは、必然的で上位階層にも使えるかもしれませんが、今は、「推論方法」について考えており、「推論として正しい確率を上げる」にはどうれないいのかが、主軸となっています。
ですから、「推論方法」について考えているとき、「推論として正しい確率を上げる」ことの方が、必然的な枠組みになります。
図15.21.思考の特性
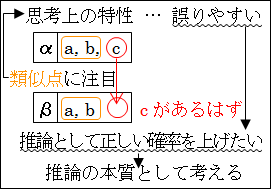
つまり、「推論」が正しく未知の事柄を導くためのものであるならば、「推論」によって「未知の事柄がどれだけ正しく導けるか」ということが、重要であり必然的に考えなければならないことです。
「類似点に注目するか否か」という枠組みを具体的になった下位階層で適用するならまだしも、抽象的な上位階層では、「必ず正しいか否か」といった枠組みの方が一般的には適していることが分かります。
そういった「推論」に本質的な性質に基づいて分解して行き、ある程度具体的になった後に、「推論」に付随する人間の特性等について考える方が良いと言えます。
したがって、「推論」の特性である「導かれた結論がどれだけ正しいか」について分解し終わって、階層が下がり具体的になった後に、最後の決め手として、「類似性」に特に注目するか否かを考えるのが効果的になります。
実際、最初にいきなり「類似点に注目する」か「類似点に注目しないか」の枠組みを設定してみると、後が続かず、様々な「推論方法」が分類し難いことを確認してみてください。
以上を踏まえて、(15.4)の解答を示しておきます。
| (15.4)「推論方法」を分類し整理するとき、最初に「類似性に注目するか否か」という基準ではなく、「必ず正しいか否か」という基準で考え始めた理由はなぜか [解答] 「推論」は、正しく未知の事柄を導くことができるという性質を持ち、それゆえに、「未知の事柄をどれだけ正しく導けるか」ということが本質的に重要になる。したがって、「推論方法」を分類し整理するという目的の下では、最初に「必ず正しいか否か」という基準で考えることが、必然的と言える。 確かに、「類似性に注目するか否か」という基準は、「推論」にも関係する。しかし、人間の思考の性質上、類似性に注目する傾向が強いため、「推論方法」の本質というよりも、「人間の思考法」の本質と考えられる。 よって、「類似性に注目するか否か」という基準よりも、「必ず正しいか否か」という基準で「推論方法」を分類し整理する方が必然的で適当である。 |
このように、対象の本質と枠組みの必然性を考えることが大切です。
3.まとめ
「上位階層に抽象度の高い枠組みを設定すること」と「対象の本質と枠組みの必然性」を併せると、上位階層と下位階層それぞれに適切な枠組みがあることが分かります。
上位階層には、上位階層に必然的な枠組みが存在し、下位階層には、下位階層に必然的な枠組みが存在します。
下位階層で適用すべき枠組みを上位階層で安易に使わないように心掛けておく必要があります。
そして、適切な枠組みの設定は、ハッキリ言って難しいです。
特に、既存の枠組みを使わずに、自分で枠組み一から構築しようとするとき、一発でいきなり上手く適切な枠組みが設定できることの方が少ないです。ある枠組みを適用して分解して行ったら、MECE にならないという壁に何度もぶち当たるはずです。そのときは、枠組み自体が間違っている可能性もあれば、枠組みを使うべき階層が間違っている可能性もあります。
このように、発散と収束を繰り返しながら、適切な枠組みが徐々にできあがってくるものです。ですから、色々と試行錯誤してください。この試行錯誤こそが、世間一般で言う「考える」ことでもあります。
以上の枠組みを設定する際の注意点をまとめておきます。
枠組み設定の注意点
|
5 論理ツリーの作り方
MECE に分解しなければならないこと、そのためには枠組みの設定が重要であることが分かったところで、論理ツリーの使い方に具体的に入って行きましょう。
まず論理ツリーを作成するときの原則は5つです。
論理ツリーの作り方
論理ツリーの特徴
|
論理ツリーの作り方の(2)(3)(4)は、MECEに分解することの重要性と方法で、今まで説明して来たことをまとめたものです。
(1)「最上位命題は、主語と述語を用いて、明確に記述する」のは、最上位命題が最終的に何を対象として理解したいかを明確にするためです。
(5)「第2階層以下のすべての命題は、原則として主語と述語を用いて記述する」のも、今自分が何を考えているのかを明確にするためです。
なお、最上位命題の場合と違って、「原則として主語と述語で記述する」理由は、一部省略しても意味が分かることがあり、また、具体的に分解して行った結果として名詞だけになる場合があっても仕方ないからです。
下位階層は、上位階層によって縛りがかけられているので、上位階層と下位階層の両方を繋げて読めば、意味が通るようになっている場合があり、その場合は一部省略しても大丈夫だからです。
ただし、これはあくまで原則です。原則には例外がつきものです。
まず、既存の枠組みを使うと、命題が主語・述語で表されずに、名詞で書かれることもしばしばあります。
例えば、先程の厚生労働省の「人生の段階」の枠組みで言えば、「幼年期」という範疇(カテゴリー)は、主語・述語ではなく名詞で表されています。
| 人生の段階 >幼年期 |
でも、よく考えてみると、名詞とは、それが何を意味するのかという定義に与えられた名前の詞です。つまり、「幼年期」は、「人生の中で、0~5歳の間」という定義に与えられた名詞です。
| 人生の段階 >幼年期:人生の中で、0~5歳の間 |
このように、既存の枠組みが名詞で表されているとき、その名詞の定義をしっかり押さえておく必要があります。そして、定義を知っていれば、命題を主語・述語で書き表す必要はなくなります。
しかし、特に既存の枠組みを使わない場合には、できるだけ主語・述語で書き表す方が良いです。
既存の枠組みを使わないということは、自分で0から考えていることを意味します。その場合、かなり厳密に名詞が定義できていないと、対象を厳密に考えることが難しくなります。
名詞の定義が曖昧だと、名詞が何を意味しているのか明確に意識できていないので、本来は含まれないはずの概念まで何となく含んで考えたり、逆に本来は含むべき概念を何となく外して考えたりしてしまうことがあります。このように、気付かぬ内に、同じ名詞でも意味がすり替わってしまうことがよくあります(多義語の誤謬に類似)。
例えば、「幼年期」が「0~5歳」と明確に意識できていないと、いつの間にか「6歳」も含んで考えてしまうかもしれません。ちゃんと「人が、0~5歳である期間」と書かれていれば、いつの間にか定義がぶれることもなくなります。
このように、自分で枠組みを作っているときは、最初から名詞が明確に定義できていることの方が少ないので、できるだけ主語と述語で書き表すようにしましょう。
また、既存の枠組みを使わずに論理ツリーをつくって他人に見せるとき、名詞だけだと定義が分からないことも多いです。
定義が分からないと、名詞が何を意味しているのかは、人によって異なる可能性があります。
例えば、「幼年期」についても、人によっては「0~3歳」くらいまでと考えている人もいるかもしれません。そうすると、厚生労働省が考えている枠組みと食い違って議論がかみ合わなくなる危険があります。
まぁ、厚生労働省が示している枠組みは有名なので、これに限ればそんなことは起き難いですが。と言うか、むしろ、厚生労働省が示す枠組みが常識として定着しているので、「幼年期」と言えば、「0~5歳」で考えるのが普通です。これから外れた定義を「幼年期」という言葉に与えて使うとしたら、それを説明しておかないといけません。
それはともかく、既存の枠組みは、学問の世界や経済活動の中で整理されます。それを多くの人が勉強して、日々の活動で使います。ですから、既存の枠組みは何を意味しているかが多くの人にとって明確であり、共通了解があるので、名詞だけでもあまり誤解は生じません。
しかし、既存の枠組みを使っていない場合は、枠組みは個人的で独自のモノであり、多くの人が知っているような一般的であったり普遍的なモノではありません。したがって、主語・述語でしっかりと書き表す方が無難になります。
さらに、名詞だけだと、この名詞に対して、誰が、何をすればいいのか、または、この名詞が何に何をするのか、といったことが分かりません。これは、概念の整理のときよりも、問題の原因究明や解決策を考えているときに、ぶつかりやすい問題になります。しかし、主語・述語で書き表されていれば、解釈の幅はぐっと狭くなり誤解が生じず分かりやすいモノになります。
ですから、各階層はできるだけ主語・述語の命題で書き表し、名詞の概念で表す場合には、その定義をしっかりと理解・共有しておかないといけません。
このようにして作られた論理ツリーの特徴は、次のようにまとめられます。
論理ツリーの特徴
|
これも今まで説明して来たことをまとめたものです。
(2)の中で、同一階層にある命題を MECE に分解する際には5つ程度の命題に止まるようにするのが望ましいのは、あまりにも細かく分解すると、その枠組みが本当に MECE になっているのか判断が難しくなるからです。
もちろん、学問的な細かい分類が必要になるなら、6個以上の命題が出て来ても一向に構いません。学問では正確性と厳密性が重要になるからです。しかし、商業活動等のように時間との勝負である部分が大きい場合には、そこまで細かくしていると計画の全体の速度に支障が出て来るかもしれません。そういった場合には、多くても5つ程度が望ましいということです。
そして、今まで見て来たのは、一般的・抽象的な対象に枠組みを当てはめて個別的・具体的な要素に分解して行く方法でしたが、このような分析の方法をトップダウン方式と言います。これは英語の top down をそのままカタカナにしただけです。和語や漢語に訳すことなく、そのまま使われて定着してしまった言葉です。top が、「頂 」や「最上層」を意味します。頂たる top 上位から down 下位へという思考の流れを表しています。
トップダウンのイメージを図で表すとこんな感じです。
図15.22.トップダウンとボトムアップ
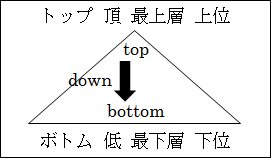
思考法だけでなく、意思決定でもトップダウン方式というときがあります。
これは、top が社長等といったお偉いさんで、down が下っ端の従業員に対する方向を表しています。つまり、上にいるお偉いさんが決定したことを、下にいる従業員が実行するという上から下への流れを言い表しています。学校で言えば、何か行事をするとき、先生が決めたことを生徒が言われた通りに実行する場合を挙げられます。
こうした場合は、日本語で「上意下達」という言葉がピッタリきます。「上」の者の「意」見が、「下」の者に「達」するということです。
しかし、思考法でトップダウン方式と言うと、「上意下達」では意味の通りが少し悪くなります。思考法についてトップダウン方式と言う場合には、「逆算」方式と言うほうがいいかもしれません。
まず、何かしらの目的があり、「その目的を達成するには、どうすればいいのか?」と考えます。自分の身近にある物事から考えて行くのが普通だとしたら、目的を達成するのに必要な物事は何かと考えるのは順序が逆になっています。
このように、トップダウン方式は、目的を達成するためには何が必要なのかという逆からの計算になるから、「逆算」方式と言えます。
論理ツリーは、主にトップダウン方式・逆算方式で考えるときに非常に強力な道具となります。
論理ツリーを使うとき、最上位命題・最上位概念に対して、枠組みを適用することで、MECE に分解します。最も一般的・抽象的な命題や概念から具体的な物事を考えているわけです。逆算方式と相性が良いのも納得できるかと思います。
ここで、トップダウンがあるのなら、その逆もあるんじゃないかと考えるのも自然な発想です。「ダウントップ方式はあるのか?」という疑問です。
残念ながら「ダウントップ」という名前はありません。しかし、「ボトムアップ」方式ならあります。要は、「ダウントップ」ではなく「ボトムアップ」と呼ぶということで、ちゃんと下から上への流れはあります。
ボトムアップ方式も、英語の bottom up をそのままカタカナにしただけです。これもトップダウン同様に日本語として定着したと言えるでしょう。bottom が、「底」や「最下層」を意味して、そこから up 「上がる」ということです。あえて日本語で言えば、「積み上げ」方式といったところです。
ボトムアップのイメージは、トップダウンのイメージとちょうど逆になります。
図15.22.トップダウンとボトムアップ
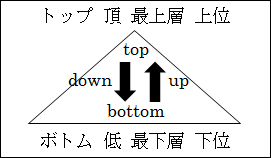
ボトムアップ方式では、個別的・具体的な物事を積み上げて、抽象化しながら、一般的・抽象的な命題や概念へと整理・分類して行くことになります。
先程、論理ツリーはトップダウン方式と相性が良いと言いましたが、枠組みを自分で作り出すとき、この積み上げ方式も必要になってきます。
トップダウン方式をまず基本として習得しつつ、慣れてきたら、ボトムアップ方式も試してみて練習するようにしておけばいいでしょう。
それでは、論理ツリーのボトムアップ方式とトップダウン方式の2つの使い方を学んでいきたいと思います。
6 ボトムアップ(積み上げ)方式
論理ツリーとは何ぞやということを長々説明して来ました。そして、対象に枠組みを適用して、より個別的・具体的な要素に MECE に分解していくのが、トップダウン方式・逆算方式でした。これが論理ツリーという道具に相性が良い方式でした。「人生の段階」にしろ、「学問の分類」にしろ、「推論方法」にしろ、このトップダウン方式で整理して、論理ツリーを作成しました。
このトップダウン方式に対して、一般的・抽象的な対象が見つかる前に、まず個別的・具体的な対象がある場合にはどうすれば良いのか、ということを考えます。
つまり、個別的・具体的な複数の対象をまとめて抽象化して行くことで、論理ツリーを作成するにはどうすればよいか、ということを学びます。
これは、トップダウン方式・逆算方式に対して、ボトムアップ方式・積み上げ方式と呼びます。
ここでは、ボトムアップ方式で高校で習う教科を分類してみましょう。
| (15.5)次の13科目を特徴に応じて、思いつく限りの分類の仕方を考えよ 英語 化学 現代文 古文・漢文 数学 政治・経済 生物 世界史 地学 地理 日本史 物理 倫理 |
合計で13科目あります。
通常、国語でまとめられている現代文と古文と漢文は、現代文と古文・漢文にバラしています。現代社会は、政治・経済と倫理を併せて薄めたような科目なので、ここでは省いています。
私大専願なら3科目で済みますが、だいたいの人は大学入試ではセンター試験を受けるので、5教科7科目や6教科8科目勉強することになります。
さて、この13科目、文系や理系といった既存の枠組みに当てはめて考えないようにするため、敢えて「あいうえお順」に並べています。これを分類・整理してみてください。
おそらく、だいたいの人は、既存の枠組みを使うつもりはなくとも、つい自分の知っている枠組みを頼りにして、各教科の共通点や関連性を見出したかと思います。つまり、このように共通点を見出してまとめるのではないでしょうか。
図15.23.科目の分類1 画像クリックで拡大

これは、複数ある対象から共通点を見出してまとめているので、抽象化にあたります。
「英語」「数学」「現代文」「古文・漢文」は文系・理系問わずに使用することが多く、言語能力や計算能力といったすべてに共通する基礎的な教科と考えて、「基礎教科」としてまとめています。一般には、「英数国」とくくられることが多いかと思います。
「日本史」「世界史」「地理」「倫理」「政治・経済」は、社会に共通する教科と考えて、「社会科」としてまとめています。
「物理」「化学」「生物」「地学」は、科学に共通する教科と考えて、「理科」としてまとめています。
個別的・具体的な教科それぞれに共通する要素を抜き出して、上位概念を抽出しています。
つまり、13科目は、「基礎教科」「社会科」「理科」という同次元の3つの上位概念に分類されています。
他にも、もう少しだけ細かく分けて、こう分類した人もいるかもしれません。
図15.24.科目の分類2 画像クリックで拡大

「社会科」がもう少し細かく分けられるぞと考えて、「社会科」という範疇(カテゴリー)ではなく、「地理歴史」という範疇(カテゴリー)と「公民」という範疇(カテゴリー)に分けます。
「日本史」「世界史」「地理」は、人間の時間軸と空間軸を学ぶという共通性に注目して、「地理歴史」としてまとめています。
「倫理」「政治・経済」は、人間の考え出した思想や仕組みを学ぶという共通性に注目して、「公民」としてまとめています。
「基礎教科」と「理科」はそのままです。
このように、分類方法はいくつも見つけ出すことができます。分類方法1(図15.22)は主に中学校まで用いられることが多く、分類方法2(図15.24)は高校で用いられることが多いというのは、多くの人が経験から知っているはずです。
では、このようにまとめたらどうでしょうか。
図15.25.科目の分類3 画像クリックで拡大
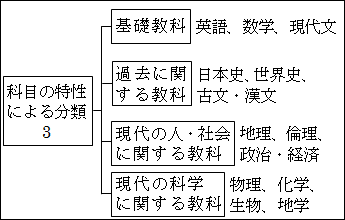
「基礎教科」では、「英語」「数学」「現代文」は変わらずに、言葉を操ったり計算したりするという基礎的な能力を養う科目という共通性に注目しているのですが、「古文・漢文」は日常では使われないという点を考慮して外しています。
その代り、「古文・漢文」は昔の言葉を学ぶということで、過去に起きた出来事を主に学ぶ「日本史」「世界史」とあわせています。過去について主に学ぶという共通性から「過去に関する教科」という上位概念を抽出し、分類・整理できます。
一方、「地理」「倫理」「政治・経済」は、現代の状況を主に学ぶという共通性から「現代の人・社会に関する教科」という上位概念を抽出できます。
「倫理」については過去の思想家を学ぶことも多いですが、今をどう生きるかを考えるために学ぶことを重視して、「過去に関する教科」ではなく「現代の人・社会に関する教科」に分類しています。ですから、「倫理」については、「過去に関する教科」に分類しても構いません。
「物理」「化学」「生物」「地学」は、現代の科学に共通する教科と考えて、「現代の科学に関する教科」としてまとめています。
さらに、「現代の人・社会に関する教科」と「現代の科学に関する教科」では、「現代に関する」という語句が重なっていることに気付きます。このことから、さらに抽象化して上位概念が導けそうだと考えられます。
図15.25.科目の分類3 画像クリックで拡大
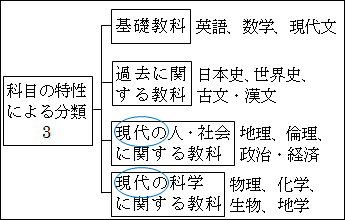
したがって、「現代に関する教科」を導けます。
つまり、「現代の人・社会に関する教科」と「現代の科学に関する教科」は、「現代に関する教科」という範疇(カテゴリー)の下位概念になります。
上位概念「現代に関する教科」の下の概念なので、「現代の」という文言を省略して「人・社会に関する教科」と「科学に関する教科」としています。
図15.26.科目の分類3' 画像クリックで拡大
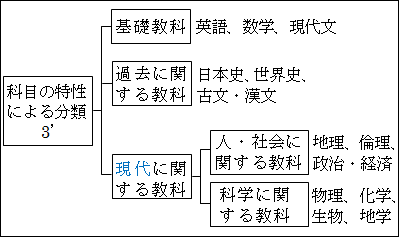
そして、同一階層は同一次元でそろえるのが、論理ツリーを作るときの約束事でした。
「現代に関する教科」は、抽象度の次元としては、「基礎教科」と「過去に関する教科」と同じ階層になります。
ここで、仮に、「現代に関する教科」が「基礎教科」と「過去に関する教科」よりも上位階層にある、つまり、より抽象的であると考えると、論理ツリーはこうなります。
図15.27.科目の分類3'' 画像クリックで拡大
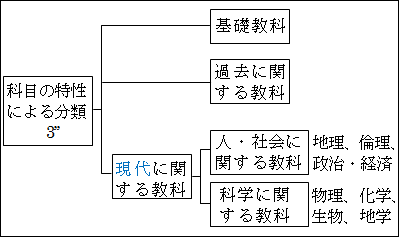
この図からは、「基礎教科」と「過去に関する教科」の上位概念がないと、第2階層で MECE に分解できていないのが明確に分かります。
図15.27.科目の分類3'' 画像クリックで拡大
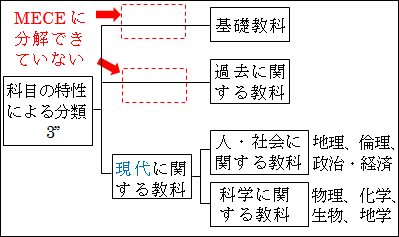
したがって、「現代に関する教科」は、抽象度の次元としては、「基礎教科」と「過去に関する教科」と同じ階層だということが納得いきます(図15.26)。
そもそも、「基礎教科」と「過去に関する教科」と「現代に関する教科」という枠組みは、同一次元で MECE に分解できているということは、直観的にも納得いくものかと思います。
もちろん、「基礎教科」と「過去に関する教科」とを合せる等して、「現代に関する教科」と同程度の次元の範疇(カテゴリー)を作り出してるのなら、それもありです。が、しかし、この両者に共通する抽象的な概念は思いつくのは難しいでしょう。
敢えて例を上げるのならば、「現代を学ぶための教科」といった範疇(カテゴリー)を抽象化してみるのはどうでしょうか。
図15.27.科目の分類3'' 画像クリックで拡大
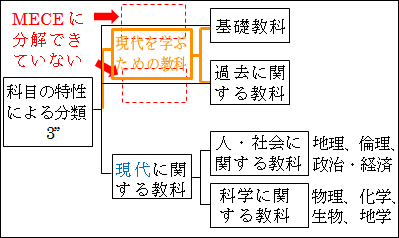
「現代」について学ぶためには、「過去」のことを知っておかないといけないし、「現代」を考えるための道具として言語や数学といった「基礎」的な能力が必要になります。
このように、「現代」を学ぶ以前に当然に知身に付けておくべき教科と考えられるため、「現代を学ぶための教科」と抽象化してみました。
これならば、「現代に関する教科」は、「現代を学ぶための教科」と同じ次元にあることになります。
ただし、もともと「現代を学ぶための教科」という範疇(カテゴリー)を抽象化して導いたのは、「現代に関する教科」が「基礎教科」と「過去に関する教科」よりも高い抽象度の次元にあると考えたからです。
ですから、「基礎教科」「過去に関する教科」「現代に関する教科」が同一階層にある分類でも同じ次元に MECE に分解できているので、この3つの範疇(カテゴリー)を同一階層に置いても、まったく問題はありません。
図15.26.科目の分類3' 画像クリックで拡大

なお、「現代に関する教科」の下の階層には、「人・社会に関する教科」と「科学に関する教科」があるのに、「基礎教科」や「過去に関する教科」の下の階層には何の範疇(カテゴリー)もないことに、気持ち悪さを覚える人もいるかもしれません。しかし、これで構いません。
上位階層に対応させて、そのすべてに下位階層がそろっている必要は別にありません。対象を理解するために論理ツリーを作っているので、十分に具体的に分解できているのなら、無理に階層をいじくり回す必要はありません。
ただ、そうは言っても、そろえたいと思う人もいるでしょう。
今から見せる操作は、上位概念を参考にしつつ下位概念を導いているので、完全にボトムアップ方式とは言えませんが、ボトムアップ方式の過程で、上位概念から下位概念を導くことの例と思って参考にしておいてください。
「基礎教科」について、「外国語」「日本語」「数の言葉」という下位概念を導けます。それぞれ「英語」「現代文」「数学」が対応します。
「過去に関する教科」について、「外国に関する歴史」「日本に関する歴史」という下位概念を導けます。それぞれ「世界史」「日本史、古文・漢文」が対応します。
図15.28.科目の分類3'-2 画像クリックで拡大
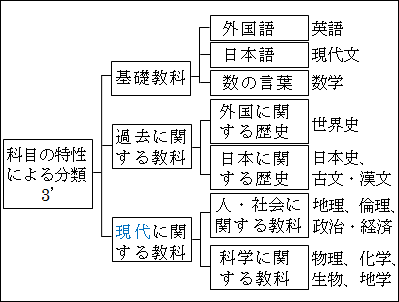
他にも切り口を変えて、「基礎教科」については、「人が話す言葉」「数の言葉」という下位概念を導けます。
「過去に関する教科」については、細分化せずにそのまま具体化するだけにして、「人の歴史」と下位概念を導くこともできます。
図15.29.科目の分類3'-3 画像クリックで拡大
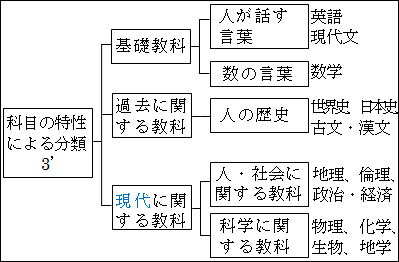
様々な分類法および枠組みがあることが分かっていただけたでしょうか。何か1つの絶対不変の答えがあるのではなく、色々な考え方、理解の仕方があるのが分かります。
しかし、どんな分類法や枠組みでも、目的に適したものでない限り、無用の長物になります。
科目の特性による分類1や分類2に慣れていると、科目の特性による分類3は、使い道があまり思いつかないかもしれません。しかし、「入試科目だけ勉強しておけばいいや」と考えている生徒に対して説明するときには、この枠組みが効果的になるかもしれません。例えば、このように説明してみましょう。
大体の人は、「基礎教科」に関して、その必要性も何となく感じており、文句を言わずにその3科目を勉強する人が多いです。しかし、入試を突破する最大の目的は、大学に入るためだけではなく、大学で学ぶためです。そして、大学での学ぶ目的は、専門的な知見を学ぶことだけではなく、現代社会に生きる上で広く物事を見渡す力を養うことも挙げられます。後者は教養というものです。
そうすると、「大学で学んだ」と言うためには、自分の専門に関係ないように思えることも、文系理系問わず「現代に関する教科」を最低限勉強しておく必要があります。
また、「現代に関する教科」は主に現代について学ぶものですが、現代は過去から連続しながら形成されたものです。したがって、「過去に関する教科」もしっかりと学んでおかないと、真の意味で現代について理解はできません。
こういったことを考えると、「自分は文系だから」、あるいは、「自分は理系だから」、「この科目は別に勉強しなくてもいい」。「大学入試で使わないからやるだけ無駄だ」と言うのは、大学の目的から外れたことを言っていることに気付きます。
目的から外れたこと、つまり、的外れなことを言う人は、馬鹿や間抜けといった言葉でくくられるのが一般的です。大学とは一般に知的活動ができる人が行く所のはずなのに、馬鹿や間抜けと一般的に言われる人が行くことになっているとは滑稽ですね。でも、最初から頭が良ければ、大学行く必要なんてないので、馬鹿や間抜けだからこそ大学へ行かないといけないと考えれば、これはこれでアリなのかもしれません。
こうした「大学の目的」を説明するとき、「文科系」と「理科系」の枠組みでは見落としがちな事柄を、「基礎教科」と「過去に関する教科」と「現代に関する教科」という枠組みでは、上手く拾い上げてくれているので、良い枠組みだと言えます。
以上が、ボトムアップ方式で論理ツリーをつくる過程の一例です。
どのような枠組みを作り出すかは、人によって様々で、使える枠組みなのかどうかは目的に応じて変わってきます。
実際、比較的自由に枠組みをつくっていたのが分かるかと思います。色々と試行錯誤しながら自分で作ってみてください。
なお、ボトムアップ方式で論理ツリーを作るときの注意点として、個別的・具体的な複数の対象をまとめることから始めているので、最初に存在している対象以外の対象については、枠組みから抜け落ちて、見落としてしまう可能性がある、ということです。
例えば、最初に13教科から開始していましたが、学校で習う教科全般に視野を広げると、「モレ」が発生することになります。
つまり、今まで考えてきた枠組みでは、13教科以外の科目である「家庭科」、「体育」、「保健」、「情報」、「芸術」といった教科は、無理矢理「現代の人・社会に関する教科」にぶち込む以外には、どの範疇(カテゴリー)にも当てはまらないことになります。
他にも、商業高校等なら「簿記」といった科目はどうなるのかといった疑問も出て来るでしょう。
と言っても、ボトムアップ方式である場合に「モレ」が生じるのが、必ずしもいつも悪いというわけではありません。
今まで考えてきた枠組みは、「13教科を分類する」という目的があって分類していました。その点では、これらの枠組みによる論理ツリーは、目的を達成できており、決して間違いではありません。
ここで言いたいことは、目的が変わって「高校で習う科目全体」に視点を広げた場合には、この論理ツリーでは、「モレ」が発生する可能性があるということは認識しておく必要がある、ということです。
このことは、どのような枠組みも、目的や状況によって、有効か有効でないかが決まるのであって、無理矢理に何にでも当てはめてやろうとしてはいけないとうことを教えてくれています。
7 トップダウン(逆算)方式
繰り返しになりますが、論理ツリーは、トップダウン方式・逆算方式で考えると相性が良いです。先のボトムアップ方式以外、これまで説明で使ってきた論理ツリーは、全部トップダウン方式で作られたものでした。
一般的で抽象的な対象が存在し、これって具体的には何なのかをを考えるときに、トップダウン方式・逆算方式で考えることになります。
したがって、一般的・抽象的な対象を具体化して行くことになります。
改めて、ボトムアップ方式と対比して違いを明確にするため、高校で学習する教科をトップダウン方式で分類してみましょう。
| (15.6)高校(普通科)で学習する教科を分類せよ |
「教科を分類する」と考えたとき、最初にどのような切り口があるでしょうか。
3 枠組み設定では、「人文科学」「社会科学」「自然科学」といった枠組みを使って学問を分類しました。もちろん、この枠組みを使ってトップダウン方式で分解してもいいです。が、ここでは、自分で1からトップダウン方式で枠組みを作ることを経験しておきたいので、既存の知識として参考にしてもいいですが、そのままは使いません。
それでは、改めて枠組みを考えるためにも、「教科」とはそもそも何なのか、ということを考えましょう。
これは、論理ツリーの原則である、対象の本質を考え必然的な枠組みを作るためです。
でも、いきなり「教科」を分類するために「教科」の本質を考えないといけない、と言われても困るでしょう。そこで先ずは、思いつきやすく考えやすい身近な事柄から始めてみます。
学校での勉強は、色々な分野の知識を学びます。
各「教科」の内容は、大学の教授や研究者を中心にして、ある程度正しい事実や法則であると認められる基礎的な知識で構成されています。言ってみれば、定説や通説といったモノで構成されています。
つまり、「教科」は、「学問のための基礎」と言い換えられます。
図15.30.教科の本質の考察
それでは、「学問」とは、どのように構成されているのでしょうか。
「学問」は、人間を中心に組み立ててられています。人間が何かを見て、気付き、考えて、まとめたものが学問となるので、当たり前と言えば当たり前です。
図15.30.教科の本質の考察

したがって、学問は、人間の視点から考えることになります。
何事も観察して考える主体である人間がいないと始まりません。
図15.30.教科の本質の考察

主体があれば客体あり。
客体とは主体の対義語で、対象のことです。人間が観察・思考する主体であるからには、観察・思考される対象が必要になります。
図15.30.教科の本質の考察

人間を中心に考えているのだから、観察・思考される対象も、主体たる人間を中心にして考えます。
図15.30.教科の本質の考察
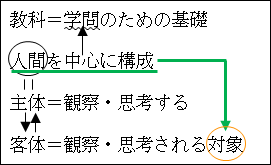
したがって、「人間が創ったもの」か「人間以外が創ったもの」かという枠組みで分解できると思い至ります。
「そのもの」と「それ以外」という枠組みの応用ですから、MECE に分解できていることも分かります。
図15.30.教科の本質の考察
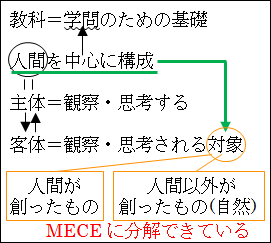
このようにして、「教科」とは何かを考えることで、「人間が創ったものを対象とする」と「人間以外が創ったもの対象とする」という枠組みの雛形を考え出すことができました。
この枠組みの雛形は、MECE に分解できているので、すべての「教科」は、このどちらかの範疇(カテゴリー)に必ず含まれることになります。
なお、「人間以外が創ったものを対象とする」という範疇(カテゴリー)では、「人間以外が創ったもの」を「自然」と書き換えられます。
これは知っておかないとできない読み換え操作かもしれませんが、「人間」と「自然」を対立させる考え方はかなり有名なので、「人間」と「人間以外」という範疇(カテゴリー)が導けた時点で、「人間以外が創ったもの」を「自然」へと書き換えることを思いつく人も多いかと思います。
ちなみに与太話になりますが、この「人間」と「自然」を対比する考え方の由来を遡ると、「神」が出てきます。
私達が学ぶ現代の学問は、絶対にして唯一の神を信仰するキリスト教の影響下にあるヨーロッパで発達しました。したがって、「人間以外が創ったもの」の「人間以外」とは、「キリスト教の神」のことです。この「人間」と「自然」を対立させる考えは、「神」が自分に似せて「人間」を創り、その他に「自然」を創造したという話に由来しています。
「神」が「人間」を含めてすべてを創り出したので、「神」を信仰し、「神」の教えに近づくために、「人間」自身が創ったモノと「神」が創ったモノを区別する考えが生まれます。
まぁ、世俗化した現代では、熱心な人を別にして、キリスト教徒でもこの区別が正しいと心の底から信じているかはやや疑問ですが、元をたどればこういうことです。
さて、「人間が創ったものを対象とする」か「人間以外が創ったもの(つまり自然)を対象とする」かという枠組みを、「教科を分類する」ために当てはめます。
図15.31.教科の分類
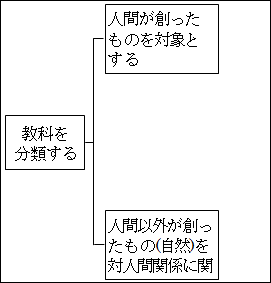
こう見ると、「文科系」と「理科系」の枠組みと似たものになりそうだなと予想できます。しかし、繰り返しになりますが、自分で枠組みを作るために、参考にすることはあっても、敢えてそのままは使いません。
「教科」の中で「人間が創ったものを対象」とするものは、どのように分解できるでしょうか。「人間が創ったもの」とは何かを考えてみましょう。
まず、思いつくのは「言葉」があるかと思います。
今現に私が話しているのを聞いているので、簡単に思いつくはずです。
他には、「道具」もそうでしょう。
今チョークで板書していますし、日頃から色々な道具を使って生活しています。
さらに他には、何があるでしょうか。私達はどのように暮らしているでしょうか。
友達と他愛のない話もすれば、音楽や運動も楽しんでいます。他には、物を買って生きています。事件が起きれば、これって正しいことなのだろうかと考えることもあります。昔を振り返ることもあるでしょう。したがって、「文化」「社会」「思想」「歴史」などなど、色々思いつきます。
| 人間が創ったもの >言葉 >道具 >文化 >社会 >思想 >歴史 |
このように、6つの範疇(カテゴリー)に分解できました。別に6つでも良いと言えば良いのですが、できるなら同一階層には5個程度までの範疇(カテゴリー)に収めたいので、抽象化してまとめられないか考えてみましょう。
「社会」と「思想」と「歴史」に共通するのは、複数の「人間」が互いに影響し「関係」し合うことで、具体的な物質だけでなく出来事等も含めて何かしらを生み出しています。
よって、「人間関係」と抽象化できます。
| 人間関係 =人間が互いに影響し関係し合って創り出す >社会 >思想 >歴史 |
「道具」と「文化」も、人間は、道具を使うことで、様々な活動を行って何かを生産し、それを楽しみます。これには、自らの身体を道具として扱うことも含めます。
したがって、「文化」は「道具」と密接に関わっているのが分かります。
ただし、「道具」と言うと何か物質的なモノに限定されるような気もするので、よりも広い意味を持たせるために、「技術」と呼びましょう。そうすると、「文化・技術」という範疇(カテゴリー)が抽象化できます。
| 技術・文化 =技術を用いて文化を創り出す >道具 >文化 |
「言葉」は「言葉」のままでいいのですが、「言語」と言い換えておきます。
理由は、別に恰好をつけたいからでもいいのですが、他の言葉に合わせて漢語を使って統一したいからです。
やまとことばである「言葉」ではどうしても日常的に発せられる音や文字にのみに注目している印象があるので、「言語」という漢語を使うことで、日常のみに収まらない広い意味での言葉を考えていることを明確にしておきたいからです。
| 言葉 ⇒ 言語 |
このように、「人間が創ったものを対象とする」教科は、「言語に関する教科」「人間関係に関する教科」「文化・技術に関する教科」に分解できました。
図15.31.教科の分類 画像クリックで拡大
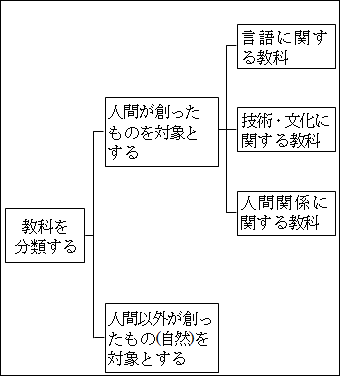
それではさらに、下位階層の各範疇(カテゴリー)を個別に検討していきましょう。
まず、「言語」についてです。
「言語」と言うと、真っ先に「日本語」が思いつくはずです。
この講義で使われている言語は日本語ですしね。そうすると、「英語」もそうだなと思いつきます。
他には、この講義を聴いて来た人は分かると思いますが、リンゴやみかんといった単語のような言葉の内容そのものよりも、論理的に正しいかといったことを考えるための言葉がありました。
「数学」はこれに分類されます。
ここで、根っからの文系だから「数学」なんて理系の範疇(カテゴリー)だし、知ったこっちゃないという人がいたら考えを改めてください。
その理由の例として、人間が数を生み出す過程に確認します。
今、「リンゴ A」と「リンゴ B」があるとします。この「リンゴ A」と「リンゴ B」は、本来別々の具体的な事物です。

それなのに私達は、別々の異なる「リンゴ」に対して、「リンゴ」が2玉あると考えることができます。
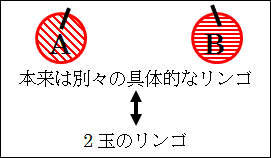
これは、「リンゴ」という1つの種類に抽象化が起きています。
そして、別々の異なる「リンゴ A」と「リンゴ B」は、抽象的な概念である「リンゴ」の範疇(カテゴリー)に当てはまる事物が2つあるからと考えているわけです。
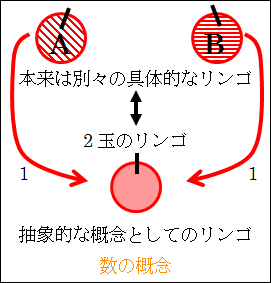
このように、「数」の概念は、個別の具体的な属性や性質を捨象して極度に抽象化することで導かれます。
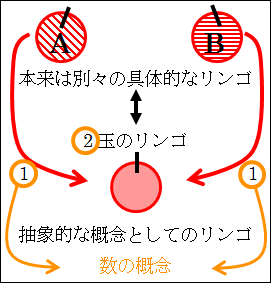
なお確認ですが、もし「リンゴ A」と「みかん B」だとしたら、「リンゴ」が2玉あるとは考えることが誤りになります。
正しくは、「リンゴ」と「ミカン」が1個ずつあると考えることになります。
これは「リンゴ」と「ミカン」の概念の範疇(カテゴリー)が違うため、「ミカン B」を「リンゴ」という抽象的な概念で処理することが適切でないからです。
しかし、「果物」という概念を用いれば、「リンゴ A」と「ミカン B」は「果物」が2つあると言えます。
このように、「数学」の基礎は元々日常で使う言葉を抽象化することで構築されていったものだと分かります。「数学」は、そういった日常の言葉では考えることが難しい抽象的思考を可能とする言葉とも言えます。
ですから、「数学」は「言語」に分類されます。
そうすると、「日本語」や「英語」といった「日常で使う言語」と、「数学」という「抽象的言語」とに分けることができる、と発想できます。
| 言語 >日常で使う言語 >抽象的言語 |
次に、「技術・文化」について考えてみましょう。
「技術」は「道具」を抽象化したものでした。「文化」はそのまま「文化」でもいいですが、「技術・文化」という概念からは、「道具」と「文化」以外にも何かを分解できそうです。
「文化」と言うと、食生活から生活様式まで色々ありますが、「生活」という範疇(カテゴリー)が導けます。
また、「文化」と言えば、絵画や彫刻、音楽といった「芸術」も導けます。
他にも、野球やサッカー、陸上等、「運動」も含まれるでしょう。
こうした「文化」は、「技術」に裏打ちされたものであることからも、「技術・文化」を上手く分解できていると分かります。
| 技術・文化 >道具 >生活 >芸術 >運動 |
最後に、「人間関係」について分解します。
「人間関係」は、「社会」「思想」「歴史」をまとめたものでしたから、これをそのまま使いましょう。
| 人間関係 >社会 >思想 >歴史 |
各分解ををまとめると、こうなります。
図15.31.教科の分類 画像クリックで拡大
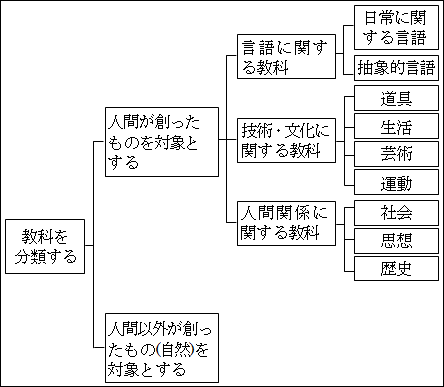
そうすると、ボトムアップ方式で分類した13教科の内、「物理」「化学」「生物」「地学」を除いたものは、このように分類できます。
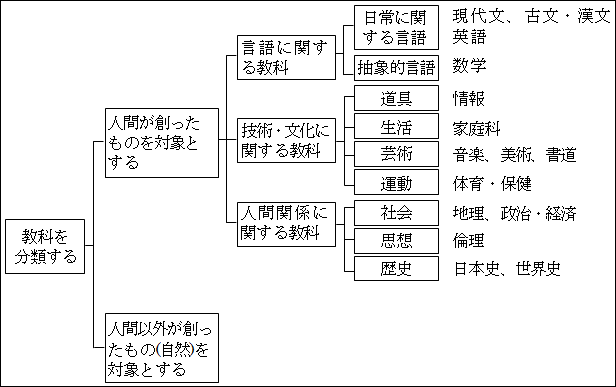
図15.31.教科の分類 画像クリックで拡大

「言語」の中の「日常で使う言語」には、「現代文」「古文・漢文」「英語」が分類されます。
「抽象的言語」には、「数学」が分類されます。
「人間関係」の中の「社会」には、「地理」「政治・経済」が分類されます。
「思想」には、「倫理」が分類されます。
「歴史」には、「日本史」「世界史」が分類されます。
このとき、「技術・文化」の中の「道具」「生活」「芸術」「運動」には、13教科の何も分類されないことになります。しかし、大学入試に使わなくとも、学校で勉強する「情報」「家庭科」「音楽」「美術」「書道」「体育・保健」といった科目があったことを思い出します。
「道具」には「情報」が、「生活」には「家庭科」が、「芸術」には「音楽」「美術」「書道」が、「運動」には「体育・保健」がそれぞれに当てはまることに気付きます。
図15.31.教科の分類 画像クリックで拡大
「人間が創ったものを対象とする」範疇(カテゴリー)の分解が終わったので、「人間以外が創ったもの(自然)を対象とする」範疇(カテゴリー)の分解に移りましょう。
「人間以外が創ったもの」すなわち「自然」を勉強の対象にする場合の「自然」とは何でしょうか。
日本的な感覚で言えば、山川草木といったところでしょう。他にも、動物も「自然」と考えられます。
こう見ると、「自然」と言えば、主に「生きているもの」を考えているのが分かります。
でも、パッと思いついたのが「生きているもの」ですが、そうではないことも容易に思いつきます。そこで、「そのもの」と「それ以外」の枠組みを応用します。
| 自然 >生きているもの >生きていないもの |
「生きているもの」が「そのもの」です。「生きていないないもの」が「それ以外」です。「生きているもの以外」ですから「生きていないもの」となります。
ですから、「生きているもの」か「生きていないもの」かに分けることにします。
図15.31.教科の分類 画像クリックで拡大
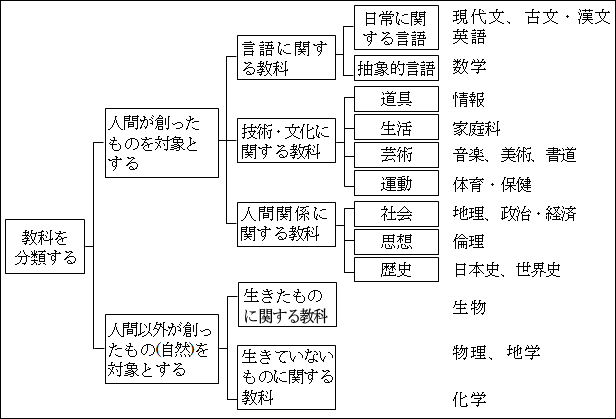
「生きているものに関する教科」には、明らかに「生物」が分類されるのが分かります。
「生きていないものに関する教科」には、「物理」「化学」「地学」が分類されるのが分かります。
もし「生きていないものに関する教科」を分解したければ、「物質の運動」と「物質の性質」に分けられます。
この分解の仕方は知っていればでき、知らなければできない、という分け方に感じるかもしれませんので、少し説明しておきます。
| 生きていないもの >物質の運動 >物質の性質 |
まず、「生きていないもの」の特徴を理解しようとするとき、考えるべき事柄は、「物質の性質」であるということは容易に発想できるでしょう。
問題は、「物質の運動」という範疇(カテゴリー)がなぜ出て来るのか、といったとこでしょう。
生物が変化したり移動したりするのは、私達も人間という生物ですから納得しやすいです。が、非生物である物質が動いたりするのは結構不思議です。そう思えるならば、「物質の運動」の法則を考えるのも、「生きていないもの」を考察する上で重要であることが分かるかと思います。
そして、「物質の運動」には、「物理」と「地学」が分類されます。「物質の性質」には「化学」が分類されます。
この説明でもよく分からなかったら、高校の勉強をすれば何となく分かるようになるので、今は聞き流しておいてください。
図15.31.教科の分類 画像クリックで拡大
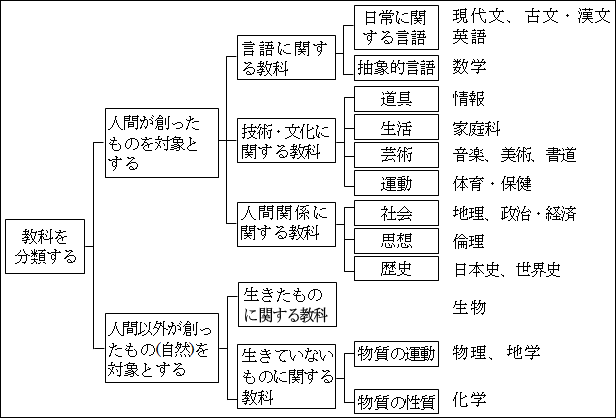
このようにして、トップダウン方式で論理ツリーを作ります。
既存の枠組みを使わずに論理ツリーを作る例を見せたかったので、結論ありきでバンバン切らずに、これって何だろうか?、という思考の過程を敢えて見せています。
実際に自分で作ろうとしたら、このような思考の過程でもまだ簡潔化されていることが分かります。上位階層と下位階層をもっと行ったり来たりを繰り返すことになります。分からないことがあれば調べて、情報を収集しなければなりません。
この思考の発散と収束の繰り返しが、対象の理解の助けにもなります。既存の枠組みを使う際でも、一度は自分の頭で考えて論理ツリーを組み立てることをおすすめします。
なお、ボトムアップ方式とは異なり、高校で習う教科を分類するという目的の下に論理ツリーを作りましたが、もし目的が「13教科」に絞って分類するというのであれば、「技術・文化」の範疇(カテゴリー)は削除できます。
と言うか、そもそも考えなくてもいいことになります。「技術・文化」について思考をめぐらさなくてもよいので、情報を収集す時間も節約できます。そして、論理ツリーが長大なものにならずに、より目的に適した論理ツリーとなります。
ですから、目的をしっかりと明確にして、目的達成思考で論理ツリーを作成するようにしてください。こういった場合には、前提条件として、「13教科のみを考えればよい」と置くことになります。
ボトムアップ方式にしろ、トップダウン方式にしろ、「教科を分類」しようと思ったら、見方や考え方によって、色々な分け方ができるのが分かります。
各科目は個別に独立していないし、見方によっては類似する教科の可能性も十分あり、どれも勉強しておく必要があるな、という気がうっすらでも持ってもらえればいいなと願っています。
8 まとめ
以上で、論理ツリーの基本的な特徴と作り方についての解説は終わりました。論理ツリーを用いることで、対象を整理しながら理解することが捗ることが分かりました。長
くなったので、改めて論理ツリーについてまとめておきましょう。
図15.1.論理ツリーの概念図 画像クリックで拡大 
論理ツリーの作り方
|
論理ツリーは、目的達成志向で、最も一般的で抽象的な最上位命題から枠組みを当てはめながら、具体的な命題へと「ダブりなくモレなく」、いわゆる、MECE に分解していきます。
各命題は、主語と述語で書き表すのが基本となります。
同一階層にある命題は、抽象度の次元をそろえておく必要があります。
論理ツリーの特徴
|

論理ツリーでは、上位階層ほど一般的で抽象的な命題が置かるので、枠組みも、上位階層には適度に一般的で抽象的な枠組みを設定することが大切になります。
そのとき、対象とは一体何のかという本質を考えるとともに、対象を何故、どのように理解したいのかといった目的を考えて必然的な枠組みを設定するようにします。
それゆえに、上位階層には上位階層に、下位階層には下位階層に、ふさわしい枠組みがあります。
枠組み設定の注意点
|
そして、論理ツリーを実際に作る段階になると、抽象的なモノから具体的なモノへという流れの下に、上位階層から枠組みを設定していくトップダウン方式・逆算方式による分解が主になります。
しかし、ボトムアップ方式・積み上げ方式もあり、具体的な物事から共通点を見い出して抽象的な物事へという流れで考える場合もあります。このときは、枠組みはあまり役に立たないことが多いです。
トップダウン方式とボトムアップ方式とは論理ツリーの作成過程で、部分的に両方用いられることもありました。
図15.22.トップダウンとボトムアップ

そして、論理ツリーは、目的に応じて、what ツリー、why ツリー、how ツリーの3種類を使い分けることになります。
目的が「構造・概念の整理」のときには、what ツリーを用います。
目的が「原因の究明」のときには、why ツリーを用います。
目的が「解決策の立案」のときには、how ツリーを用います。
この章で見て来た論理ツリーは、構造・概念の整理を主にするための what ツリーでした。対象を理解するために、色々と試行錯誤しながら分解していきましたね。
そして、why ツリーと how ツリーとでも論理ツリーの作り方の基本は変わりませんし、what ツリーは要所要所で使われます。原因を考えているときも、解決策を考えているときでも、よく分からない対象や概念が出てきたら、原因や解決策を分析するためのツリーとは別に、what ツリーで分析することになるからです。
以上で、論理ツリーの基本と why ツリーの作り方の説明を終わります。それでは、いよいよ次からは、why ツリーを用いて、問題の原因分析をして行きます。
前頁:第14章 問題と解決
ページトップへ:第15章 論理ツリー― what ツリー―
次頁:第16章 論理ツリー― why ツリー―