前頁 |▼| 次頁
第6章 仮説推論
演繹法と枚挙的帰納法、つまり、狭義の帰納法で、正しい推論の方法を学習しました。前提から結論をどのように論理的に推論するかが明らかになりました。そして、今までの話は前提が真であるものとして進めて来ました。また、演繹法では何か新しい考えを創造することはできず、狭義の帰納法でも、前提が抽象化された考え以上のものが創り出されにくいことは難しかったです。
そこで、新しい考えを創り出すのに役立つ推論、すなわち、仮説推論ついて学びます。これは、そもそもある出来事がなぜ起こるのかといった疑問やその理由を説明する考えを推論する方法でもあります。
なお、この仮説については、第 II 部 論理的な問題解決でも、よく使います。また、第III部 教養と学問・科学 第25章 科学の方法も参考になります。話が難しいかもしれないので、一度で理解できなくとも、「仮説」という考え方に出会う度によく見直して徐々に慣れて行けばいいです。
| 目次 |
| 1 仮説とは1 2 仮説推論と演繹法の相違点 3 仮説推論の方法 仮説形成と仮説検証 4 演繹法による予言 観察可能な事実 5 帰納法による検証 6 まとめ 補足 説の種類 テキストのダウンロード[詳細] 通常版 既述版 |
| ADs |
1 仮説とは
真だと分かる前提から正しく推論して結論を導く推論方法が演繹法と狭義の帰納法でした。ここからは、演繹法と狭義の帰納法を組み合わせて、新しい概念や命題を導くことを目指します。帰納法を用いているので、推論による結論は必ずしも真とは限りませんが、何か新しい概念や事象を考える場合には、論理が飛躍することも避けられません。
このように、既存の知識を基にして、観察事実を説明付けるような考えを導く推論方法を、仮説推論と言います。英語では、abduction と言います。日本語でも仮説推論よりもカタカナのままアブダクションとか仮説形成と呼ばれることが多いですが、あまり英語やカタカナを使いたくないので、仮説推論と呼ぶことにします。
この仮説推論は、アリストテレスが既に演繹法と帰納法と共に紹介していましたが、長い間あまり注目されてきませんでした。演繹法と帰納法が17世紀頃までにかなり整理されていたのに対して、仮説推論が再度表舞台に出るのは19世紀まで待たないといけませんでした。
19世紀後半にアメリカの哲学者であるパースが、アリストテレス以来の仮説推論を整理しました。彼は、学問および科学や日常の論理的思考において、純粋に演繹法と帰納法だけで推論しているわけではないことを分析しました。何か事象を観察したときに、それを前提としつつも、演繹法や狭義の帰納法では明らかな論理的な飛躍や誤りとなる結論を導いているということです。ちなみに、パースのようなアメリカの思想の流れをプラグマティズムと言います。イギリス経験論の流れを引き継ぎつつ、アメリカ流に多様な問題を解決するための実践に重きを置いています。
話を戻して、つまり、仮説推論とは、
まず、前提となる事実・事象を観察・発見する。
そこから純粋に推論のみしているのではなく、何故このような観察事実が起きているのだろうかという疑問を持つ。
疑問に対する答えを探す。つまり、何故これが起きたのか理由の説明を試みる。
その理由の説明を行うときに、演繹法や帰納法が組み合わせて推論している。
という推論方法です。
そして、観察事実に対する合理的な説明を仮説と言います。英語では、hypothesis と言います。なお、合理的とは論理的に筋の通ったという意味で捉えてもらえれば結構です。事実に対する仮の説明ですね。
何故に仮の説明なのかと言えば、正しいか間違っているかが、ハッキリと分からないからです。正しいかどうか分からないが、論理的にはそう説明できるということから「仮の」説明になっているということです。演繹法でも、前提が真であると最初に仮定して正しく推論すれば、論理という面だけを見ると正しくなったのと同じです。論理的に説明はできているが、それが実際に事実と合致しているかは分かりません。したがって、仮説推論は、この仮説を形成するための推論方法と言えます。
仮説みたいな事実を正しく説明しているか分からないものなんか作ってどうするんだ、と思う人もいるかもしれません。
しかし、日常生活を振り返ってみれば、始めから前提が正しいと分かっていることの方が少ないことは、すぐに気付くかと思います。実際、ある事実や事象を観察したとき、よく分からないけど、こうじゃないのかなと勝手に推測したりすることが多いはずです。
そして、この推測は、必ずしも論理的思考によって導き出されているとは限りません。つまり、演繹法や狭義の帰納法による推論の形式に当てはまるような正しい推論となっているとは限らないということです。
前提がすべてそろっていない、またはそろっているか分からないのに、演繹法を用いて推論はできません。同時に、これは、前提が限られているのに帰納法による推論もできないことも意味します。
最初の仮説を形成する段階では、論理的思考というよりも、自分が今まで経験してきたことや持っている知識から、何となく「こうじゃないかな?」と説明を試みていることが多いです。
また、科学の法則や理論で、正しいものだと無条件に受け入れているモノも、厳密に言えば、仮説です。この事実はこう合理的に説明できる、という仮定をいくつも積み重ねて科学はできています。帰納法で見た様に、この世のすべての場合を調べ尽くすことは現実には不可能です。だから、仮説を崩壊させるような事実が新たに観察される可能性は常にあります。実際そういうことは人類の歴史の中で繰り返されています。
つまり、今現在は仮説を否定する事実が見つかっていないから、理論は正しいものとして利用しているだけなのです。科学ですら暫定的な正しさでしかありません。こうした仮説を扱う際の注意点は、第III部 教養と学問・科学の実証と反証で詳しく説明します。とりあえず今のところは、学問や科学でも仮説から始まって正しさを確認しているのだ、ということだけでも知っておいてください。
以上から、仮説の特徴が見えてきました。
最初に、仮説は観察事実に対する合理的な説明である、ということです。
仮説は、観察された事実そのものでも、単なる事実を集めたものに過ぎないのではありません。仮説とは、観察事実がなぜ起きたのかを説明したものだということです。この点で、枚挙的帰納法つまり狭義の帰納法が、観察事実そのものだったり、単に事実を集めたものであることと異なります。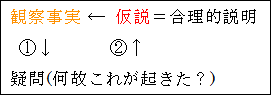
次に、仮説は必ずしも正しい説明とは限らず、事実と合致しない誤った説明である可能性がある、ということです。
仮説は、観察事実の説明のために、前提を自分で勝手に置いて推論したものなので、実際に事実を確認したら間違っていたというコトが常に起き得るということです。なお、実際に事実を直接確認することができない場合も多くあります。
こうした仮説推論の特徴を踏まえて、論理的に正しく推論する方法と、その推論で導かれた仮説をどうやって正しいものと証明するのかを見て行くことになります。
2 仮説推論と演繹法の相違点
さて、仮説とは何ぞやということが分かったところで、実際に仮説を推論する方法を考えてみましょう。(6.1)を見てください。
| (6.1)次の推論が成り立つような前提を答えよ <前提1> ある町で皆に深く礼をされている人を見た <前提2> [結論] よって、その人は町長に違いない |
この場合、「ある町で皆に深く礼をされている人を見た」ことから「その人は町長に違いない」と推論するためには、「皆に深く礼をされるならば、その人は町長だ」、または「その人が町長ならば、皆に深く礼をされる」、という2通りの前提が考えられます。
| (6.1)次の推論が成り立つような前提を答えよ <前提1> ある町で皆に深く礼をされている人を見た <前提2> [結論] よって、その人は町長に違いない →(6.1.1) 皆に深く礼をされるならば、その人は町長だ →(6.1.2) その人が町長ならば、皆に深く礼をされる |
前提2が、(6.1.1)「皆に深く礼をされるならば、その人は町長だ」であるとしてみます。
そうるすると、演繹法の条件法の三段論法、つまり仮言三段論法の推論形式となります。
| 前件肯定規則 <前提> P ⇒ Q <前提> Pである (前件肯定) [結論] よって、Q である |
前提2とした(6.1.1)「皆に深く礼をされるならば、その人は町長だ」が、大前提となります。
そして、前提1「ある町で皆に深く礼をされている人を見た」ことが観察された事実ですが、これが大前提の前件を肯定していることになります。
したがって、前件肯定になるので、結論「その人は町長に違いない」を推論することができます。
つまり、これは、三段論法の中の条件法の前件肯定規則を満たしているので、推論の形式として正しいです。
| (6.1.1) <前提1 > ある町で皆に深く礼をされている人を見た(観察事実=小前提) <前提2> 皆に深く礼をされるならば、その人は町長だ(大前提) [結論 ] よって、その人は町長に違いない 演繹法の仮言三段論法(前件肯定規則) → 正しい推論の形式 |
では、前提2が(6.1.2)「その人が町長ならば、皆に深く礼をされる」だとしたらどうでしょうか。
そうすると、これは後件肯定の形になります。
前提2とした(6.1.2)「その人が町長ならば、皆に深く礼をされる」が、大前提となります。
そして、前提1「ある町で皆に深く礼をされている人を見た」ことが観察された事実ですが、これが大前提の後件を肯定していることになります。
したがって、後件肯定になるので、結論として「その人は町長に違いない」と推論することは正しい推論とは言えず、論理的に誤りでした。
| (6.1.2) <前提1 > ある町で皆に深く礼をされている人を見た(観察事実=小前提) <前提2> その人が町長ならば、皆に深く礼をされる(大前提) [結論 ] よって、その人は町長に違いない 演繹法の仮言三段論法(後件肯定の誤謬) → 正しい推論とは言えない |
三段論法の条件法において、後件肯定は推論の結果として、結論が必ず正しいとまでは言えませんでした。もちろん、調べてみた結果として、結論「その人は町長に違いない」が正しいということが分かる可能性はあります。しかし、推論自体から結論「その人は町長に違いない」が正しいということは言えないということです。
実は、この仮言三段論法の後件肯定が、仮説推論となります。
無論、演繹法の視点から言えば、後件肯定による推論は誤りとなります。でも、仮説推論と考えると、一定の条件が付されますが、許容される推論となります。
とりあえず、改めて、仮説推論の推論形式をまとめておきましょう。
| 仮説推論 <大前提> P ⇒ Q <小前提> Q である (観察事実) [結論] よって、P である (仮説) 仮言三段論法の後件肯定 → 演繹法では正しくない推論 → 仮説推論では許容される推論 |
このような前件肯定と後件肯定の違いを、日常で実際に論理的思考を用いて推論する際に、生じる問題から考えてみたいと思います。
(6.1)に話を戻します。
前提2は、(6.1.1)「皆に深く礼をされるならば、その人は町長だ」、または(6.1.2)「その人が町長ならば、皆に深く礼をされる」、という2通りが考えられました。
前提1「ある町で皆に深く礼をされている人を見た」から、結論「その人は町長に違いない」を「正しく推論」するためには、演繹法の三段論法を使用する必要がありました。なぜならば、演繹法には、前提が真で推論が正しければ必ず結論も正しくなるという性質があるからです。
そこで、前件肯定規則を使えば、前提2は自動的に(6.1.1)「皆に深く礼をされるならば、その人は町長だ」だと導けます。しかし、前提1「ある町で皆に深く礼をされている人を見た」は、観察された事実なので真となるの問題ありませんが、前提2であり大前提である(6.1.1)「皆に深く礼をされるならば、その人は町長だ」が、実際問題として真と言えるのでしょうか。
今までの例題では、あらかじめ前提の真・偽の判定ができており、常に前提は真だとして推論してきました。しかし、現実問題として、(6.1.1)「皆に深く礼をされるならば、その人は町長だ」という命題は正しいコトとして使っても問題はないのでしょうか。この(6.1.1)「皆に深く礼をされるならば、その人は町長だ」は、現実で正しいことだと言うにはちょっと問題ありな命題かと思われます。
少し考えれば分かるのですが、「皆に深く礼をされる人」とは、何も「町長」に限られないわけです。「市長」や「県知事」かもしれない、いやいや「総理大臣」かもしれない。はたまた「社長」かもしれない。とにかく、「偉い人」なのは間違いないのでしょうが、「町長」に限定することは難しいかと思われます。だとすると、推論の形式は正しいことになりますが、推論の前提となる命題の内容が正しいとは言えないことになります。
前提が真で、推論が正しければ、必ず結論も正しくなるのが演繹法でしたが、もし前提が真でない、つまり偽ならば、推論が正しくとも必ず結論も正しくなるとは限らないことになります。このように、前提2に(6.1.1)「皆に深く礼をされるならば、その人は町長だ」という必ずしも真とは言えない前提を置くと、推論が正しくとも、前提が真とは言えないので、結論が正しいかどうかは分からないコトになってしまいます。
では、(6.1.1)に対して、(6.1.2)「その人が町長ならば、皆に深く礼をされる」が前提2になる場合はどうでしょうか。
推論自体は後件肯定になっているので、演繹法として見るならば、誤りであることは自明です。しかし、前提2となる(6.1.2)「その人が町長ならば、皆に深く礼をされる」の命題自体の内容を考えると、(6.1.1)の場合と異なり、真だと言えそうです。「町長」である人は、偉い人なのだから「皆に深く礼をされる」ことは当然に正しいと思える内容となってるからです。
そうすると、演繹法による推論としては誤りだが、前提の正しいかもしれないことになります。
こうして考えると、(6.1.1)も(6.1.2)も正しくない理由は違うが、いずれも問題のある推論だと分かります。同時に、(6.1.1)と(6.1.2)で、正しいとできない理由の違いが見えてきました。
(6.1.1)「皆に深く礼をされるならば、その人は町長だ」では、演繹法による推論は正しいが、前提が真とは必ずしも言えない。
(6.1.2)「その人が町長ならば、皆に深く礼をされる」では、演繹法による推論は正しくないが、前提が真と言えるかもしれない。
| 演繹法による 推論 | 前提 | |
| (6.1.1) | 正しい (前件肯定) | 必ずしも 真ではない |
| (6.1.2) | 正しくない (後件肯定) | 真 かもしれない |
どちらにしても演繹法で考えると正しいとは言い切れない推論になることになります。
そして、演繹法による推論の形式が(6.1.1)であり、仮説推論の推論の形式が(6.1.2)であることが分かりました。
最初に、仮説推論を英語でアブダクション(abduction)と言うと紹介しましたが、これで納得が行きます。
abduction とは、そもそも
ab =「離れて」
duct =「導く」
ion =「こと」
ですから、abduction を英英辞典で調べると、「誰かをその意志に反して無理やり連れ去る行為」と出てきます。これを踏まえて英和辞典では、「誘拐・略取」と和訳が紹介されていることが多いです。論理的思考でabduction という用語を使うとしたら、「正しい形式から離れて、無理やり推論する行為」といった具合になるでしょうか。ここでも正しい形式とは、もちろん演繹法のことです。演繹法による推論と考えると、仮説推論は、正しくない推論の形式で推論しているわけです。
これはアメリカ人の知人に対して、abduction という言葉を見ても直感的にピンとこないと話してた時に、覚え方というかイメージみたいな感じで言われたことです。ちなみに、仮説推論を整理したパース自体は、abduction という用語について一言述べています。パース曰く、アリストテレスの文献の誤記をギリシア語から英語に翻訳したからそうです。というわけで英語を母語としない我々としては、abduction という言葉自体にこだわらず、その推論方法をしっかりと理解できていればいいでしょう。
3 仮説推論の方法
仮説形成と仮説検証
演繹法と仮説推論の相違点が明確になったところで、いよいよ仮説推論を具体的に見て行きたいと思います。つまり、(6.1.2)の場合の演繹法による推論としては正しくないが前提が真かもしれない場合の推論をどう考えるべきなのか、ということです。
| (6.1.2) <前提1> ある町で皆に深く礼をされている人を見た (観察事実=小前提) <前提2> その人が町長ならば、皆に深く礼をされる (大前提) [結論] よって、その人は町長に違いない (仮説) 演繹法の仮言三段論法(後件肯定) → 正しい推論とは言えない → 仮説推論では許容される推論 |
| 仮説推論 <大前提> P ⇒ Q <小前提> Q である (観察事実) [結論] よって、P である (仮説) 仮言三段論法の後件肯定 → 演繹法では正しくない推論 → 仮説推論では許容される推論 |
そもそも仮説推論とは、何だったでしょうか。それは、観察事実に対する合理的な説明である仮説を形成するための推論方法です。 (6.1.2)に当てはめて考えると、
観察事実(小前提)「ある町で皆に深く礼をされている人を見た」に対する合理的な説明である仮説が、結論「その人は町長に違いない」である、ということになります。
この仮説を導くために、観察事実(小前提)「ある町で皆に深く礼をされている人を見た」から、仮説である結論を推論するために、「その人が町長ならば、皆に深く礼をされる」を大前提として仮定しています。
ただし、仮説は、正しいかどうか分からないが、そう説明できるというものでした。したがって、仮説である結論「その人は町長に違いない」が実際に正しいかどうかは分からないわけです。それでも一応は、観察事実(小前提)「ある町で皆に深く礼をされている人を見た」と大前提「その人が町長ならば、皆に深く礼をされる」を組み合わせて推論すれば、結論「その人は町長に違いない」を導くことができる、ということです。
これが推論によって仮説を創り出している段階です。つまり仮説形成の段階です。
なぜ仮説推論なんかするのか、前提から演繹するればいいじゃないか、と思うかもしれません。しかし、実際に人が前提から何か結論を推論するとき、純粋に演繹法だけや狭義の帰納法だけに頼っているわけではないからでした。何かを推論するときに必要な情報が、常に完全にすべて揃っていることの方が少ないです。このように不確実で不足な情報を前提として何かしら推論しなければならないとき、仮説推論が威力を発揮することになります。
とはいえ、仮説推論は前提を自分で勝手に仮定して結論を推論しているとも言えます。その仮説である結論と前提が正しいかどうかは分からないので、このままでは議論や学問において説得的ではありません。自分で勝手に仮定した前提を使って推論していいのならば、極論何でも主張したい放題になります。
そこで、仮説が本当に正しいかどうかを確かめる必要があります。これが仮説検証の段階です。
仮説が本当に正しいかどうか検証してみて、正しいコトが分かれば、仮説推論が正しいと言えることになります。それでは仮説を検証するにはどうすればよいのでしょうか。
(6.1.2)の仮説推論は、
観察事実(小前提)「ある町で皆に深く礼をされている人を見た」から、
その理由として、結論「その人は町長に違いない」を推論しており、
それを支える大前提が、「その人が町長ならば、皆に深く礼をされる」である
というものです。
この仮説における一番の重要な問題は、推論の結果である結論「その人は町長に違いない」が正しいかどうかです。これが観察事実(小前提)「ある町で皆に深く礼をされている人を見た」に対する合理的な説明だからです。そして、仮説が正しいかどうかは、実際に「その人が町長である」を証明すればよいことになります。この場合では、実際に深く礼をしていた人達に「その人が町長である」かどうかを尋ねてみればいいわけです。
そこで、「その人が町長である」ことが確認がとれれば、仮説は正しいことが証明されたことになります。
つまり、観察事実(小前提)「ある町で皆に深く礼をされている人を見た」から、その理由として結論「その人は町長に違いない」を推論したことは正しいと言えるということになります。
もし、「その人は町長ではない」、例えば「その人は市長である」といったことが確認されると、仮説は間違っていたと証明されることになります。
つまり、観察事実(小前提)「ある町で皆に深く礼をされている人を見た」から、その理由として結論「その人は町長に違いない」を推論したことは正しくなかったと言えるということになります。
このようにして、仮説が正しいかどうかを確かめる仮説検証を行うことで、観察事実(小前提)から、その理由として結論を推論する仮説推論が正しいかどうかが判断できます。
そして、正しいかどうかを確かめておらず、その真偽が分からない仮説推論は、意味があまり無いことになります。
もちろん、検証されていない仮説は、仮りの説明としては意味がありますし、1つの考え方の指針としても役に立ちます。でも、そこ止まりです。検証されていない仮説を主張するだけでは、他人を説得することは難しいです。自分と同じ意見を持っている人なら納得もするでしょうが、そうでない人は、「まぁ君がそう思うならいいんじゃないのか」と相手にされないでしょう。
したがって、仮説推論では、仮説検証がなされていることが、その主張を支える上で重要な要素になります。
以上のように、仮説推論は2つの段階があることが分かりました。
| 仮説形成:仮説の創造…観察事実(小前提)から、その理由の合理的な説明として結論を推論 ↓ 仮説検証:仮説が正しいかどうかの確認…結論が正しいことを確かめる → 結論が真 ⇒ 仮説は正しい(誤りではない) → 結論 が偽 ⇒ 仮説は誤り |
1つ目は、仮説形成の段階で、主張を組み立てる段階です。仮説を創造するために、観察事実(小前提)から、その理由の合理的な説明として結論を推論する段階です。
2つ目は、仮説検証の段階で、形成された仮説が実際に正しいかどうかを確かめる段階です。結論が正しいことを確かめることで仮説が正しいか確認する段階です。
この2つの手順を踏んで、
結論が正しければ、仮説は正しい、または少なくとも誤りではない、
結論が正しくなければ、仮説は誤りである。
ことが分かります。
4 演繹法による予言
観察可能な事実
仮説推論には、仮説形成段階と仮説検証段階があり、仮説推論が正しい推論であると言えるためには、仮説検証が重要になることは分かりました。ただ問題は、仮説検証でいつも仮説である結論を直接観察できるとは限らないことです。
どういうことか。(6.1.2)では、仮説である結論「その人は町長に違いない」を直接人に尋ねることで、それが正しいかどうかを直接確認することが、偶々ですができました。しかし、世の中では仮説である結論を直接確認できない場合も多いです。
そこで、仮説である結論が正しいと確認できたと言える事実を直接に観察することができないのなら、どのようにして仮説推論が正しいか正しくないかを決めたらいいのかということが問題になります。
例えば、「海辺が近くない陸地で魚の化石が発見された」とします。
仮説推論で、「海辺が近くない陸地で魚の化石が発見された」という観察事実(小前提)から、仮説たる結論「この一帯の陸地は昔海であった」を形成したとします。
この仮説推論の大前提は、「この一帯の陸地は昔海であったならば、この一帯の陸地は昔海であった」ということになります。(6.2)次の仮説推論の検証方法は何か
<前提1> 海辺が近くない陸地で魚の化石が発見された (観察事実=小前提)
<前提2> この一帯の陸地は昔海であったならば、海辺が近くない陸地で魚の化石が発見される(大前提)
[結論] よって、この一帯の陸地は昔海であった (仮説)
この仮説が正しいことを検証するには、実際に、結論「この一帯の陸地は昔海であった」ことを観察すればいいことになります。しかし、「陸地がかつて海であった」ことそれ自体を実際に調べることは不可能です。
なぜならば、観察事実(小前提)からも分かる通り、「今そこは陸地になっている」からです。そして、私達は現在タイムトラベル等できないわけですから、昔に戻って「そこがかつて海であった」ときの状態を直接観察することはできません。
仮説が正しいと確認できる事実を直接観察できないということは、仮説検証ができないということになります。それでは、仮説検証ができないのだから、この仮説推論は意味のないものになってしまうのでしょうか。もしそうなら、無意味なモノである論理的思考も推論も、わざわざ学ぶ必要はないでしょう。この講義自体も無駄になります。そんなことは私は認めたくありません。ですから、何か仮説検証ができる方法が無いか考えてみたいと思います。
そこで考え方を変えて、直接観察できないのならば、間接的に観察することはできないかと考えてみましょう。つまり、直接的に仮説検証できないモノを、間接的に仮説検証できる形にするということです。そして、それは、仮説検証を可能とする観察できる事実を導き出すことができるようにすることと言えます。
まず確認ですが、直接観察することは、仮説のその事実自体を観察することを意味しました。
図6.1.仮説検証と観察可能な事実 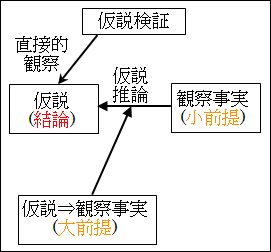
これができないので困った、となるわけです。
そこで、何かが存在するならば、それに付随する要素も存在する、ということを利用します。
これは、仮説である結論を直接観察できなければ間接的に観察をしようという試みです。結論の事実が実際にあるとすれば、その事実が持っているある要素も観察できるはずだ、と考えているわけです。そして、その要素を観察することで、結論の事実が存在することが証明できたと言ってもいいとしているわけです。
つまり、間接的に観察することが正しいと言える論理構造は、
まず、仮説である結論を真と仮定する。
次に、仮説である結論が真とすれば、結論が持つある要素が観察されるはずだ。
したがって、その要素が観察されれば、仮説である結論の事実が存在すると言える。
ということです。
日が射したとき、そこに人が立っていれば影ができます。背後に人がいるか確認しなくてもその影が確認できれば、そこに人が立っていることが分かるものです。「何かが存在するならば、それに付随する要素も存在する」とは、「人」が存在すれば、それに付随する要素である「影」も存在するということです。振り向けない等の条件によって「人」を直接観察できなくても、「影」を観察できれば、間接的に「人」が存在することが分かる、ということです。
それでは、実際に、(6.2)の仮説である結論「この一帯の陸地は昔海であった」を真と仮定してみます。(6.2.1)観察可能な事実の予言
<前提1> (6.2の仮説[結論]) 真
この一帯の陸地は昔海であった ← 真と仮定
仮説である結論を真と仮定したら、それに付随する要素として、何が観察されるでしょうか。
もともと、観察事実である小前提「海辺が近くない陸地で魚の化石が発見された」ことから、仮説である結論 「この一帯の陸地は昔海であった」を仮説推論したわけですから、観察事実である小前提「海辺が近くない陸地で魚の化石が発見された」が観察されることが当然に予測されます。
もし、仮説である結論 「この一帯の陸地は昔海であった」から小前提「海辺が近くない陸地で魚の化石が発見された」が観察されることが予測されないならば、(6.2)で観察事実である小前提「海辺が近くない陸地で魚の化石が発見された」から仮説である結論「この一帯の陸地は昔海であった」を仮説推論した理由がなくなってしまいます。
ということで、「海辺が近くない陸地で魚の化石が発見された」は、仮説形成段階である(6.2)では観察事実である小前提でしたが、仮説検証可能な観察事実導出段階である(6.2.1)では結論となります。そして、これが、仮説から予言される観察事実です。これが観察されれば、仮説検証を経て、正しい仮説推論だったことが分かると言えるようになります。(6.2.1)観察可能な事実の予言
<前提1> (6.2の仮説[結論]) 真
この一帯の陸地は昔海であった
[結論 ](6.2の観察事実=小前提)
よって、海辺が近くない陸地で魚の化石が発見された
(仮説から予測される観察事実)
しかし、(6.2.1)の前提1と結論だけでは、論理が飛躍しているように感じます。
(6.2)の仮説推論では、観察事実である小前提「海辺が近くない陸地で魚の化石が発見された」に加えて、大前提である「この一帯の陸地は昔海であったならば、海辺が近くない陸地で魚の化石が発見される」を用いて推論していました。これが結論を導くための根拠の1つになっているから推論できたわけです。
(6.2.1)仮説検証可能な観察事実を導出する段階でも、「この一帯の陸地は昔海であったならば、海辺が近くない陸地で魚の化石が発見される」は、大前提として機能します。(6.2)の仮説形成段階で、結論を導くための根拠の1つになっていたわけですから、仮説検証をする上で外してはならない前提と言えます。(6.2.1)観察可能な事実の予言
<前提1> (6.2の仮説[結論]) 真
この一帯の陸地は昔海であった
<前提2>=(6.2でも大前提)
この一帯の陸地が昔海であったならば、海辺が近くない陸地で魚の化石が発見される
[結論] (6.2の観察事実=小前提)
よって、海辺が近くない陸地で魚の化石が発見された
仮説から予測される観察事実
こうして見ると、これは演繹法の仮言三段論法の前件肯定となっています。
前提1「この一帯は昔海であった」が、前提2かつ大前提の「この一帯の陸地が昔海であったならば、海辺が近くない陸地で魚の化石が発見される」の前件「この一帯の陸地が昔海であった」を肯定しています。したがって、結論「海辺が近くない陸地で魚の化石が発見された」は、大前提の後件であるので、必然的に正しい推論となります。
図6.1.仮説検証と観察可能な事実 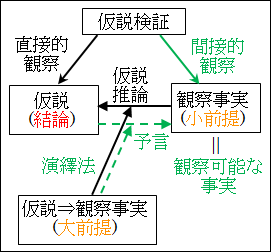
そして、実際に結論の「海辺が近くない陸地で魚の化石が発見された」が、正しいことを確認してみます。
結論「海辺が近くない陸地で魚の化石が発見された」は、元々(6.2)の仮説形成段階では最初の疑問の始まりである観察事実(小前提)だったわけですから、正しいことは自明です。つまり、結論は真に決まっています。
だとすると、前提1と前提2を真と仮定して、結論を演繹法によって推論してみたところ、推論の方法も正しく、結論も正しいことが分かり、どこにも矛盾がないことになります。つまり、仮説を真と仮定して、それを前提としても間違った推論や結論を導かないことが明らかになりました。それならば、真と仮定したことは絶対に正しいとは確信をもって言えないまでも、明らかに間違っているとも言えなさそうです。
このように演繹法を応用して検証された仮説は、正しいものとして取り扱うことにします。正しいものとして取り扱うとは、明確に間違ったものとして否定されていないという意味で、正しいからです。
(6.1.2)と(6.2)の違いは、仮説である結論の事実を直接的に観察できるか否かによって生じています。
(6.1.2)の場合には、実際に人に尋ねることで、「その人は町長である」ことが確認できました。つまり、仮説を直接的に観察できました。
(6.2)の場合には、実際に「この一帯の陸地が昔海であった」ことが確認できませんでした。つまり、仮説を直接的には観察できませんでした。
そこで、あえて仮説を前提として真であると仮定し、演繹法による推論で、元々の観察事実(小前提)を結論として導くように論理を組み立てます。
仮説が真だとしたら、当然に観察される事実を演繹法によって予測して、それを観察しているわけです。仮説を直接的には観察できていませんが、仮説に付随する事実を観察することで、仮説が観察できたとしています。これが、仮説の事実を間接的に観察することの意味です。観察可能な事実の予言←演繹法の利用
<小前提> 仮説形成段階の仮説[結論]
Pである (真と仮定)
<大前提> 仮説形成段階でも大前提
P ⇒ Q
(仮説形成段階でも使用 真と仮定)
[結論] 仮説形成段階の観察事実=小前提
Qである
(仮説から予測される観察事実)
仮説推論の最初の段階は、仮説形成段階でした。仮説形成によって、観察事実から、その事実を合理的に説明する仮説を構築します。
続いて、仮説検証段階に移りますが、仮説検証をする上で、仮説を直接的に観察できない場合があります。直接的に観察できないのならば、間接的に観察するようにします。
仮説を真として仮定します。そして、その真とした仮説を前提に、演繹法によって、推論して結論を導きます。この結論が予言です。仮説が正しいなら、つまり、仮説の事実が実際に存在するのならば、当然に結論の事実が観察されると予測できるということです。こうして結論は、予言され観察可能な事実となります。この予言された結論である観察可能な事実を実際に観察できるか否かで仮説を検証します。
5 帰納法による検証
観察可能な事実
このようにして、直接的に観察できない仮説については、間接的に観察すればいいのかが分かりました。そして、どうすれば、何を観察すれば観察ができたと言えるのかも具体的に分かりました。日常の場面だけでなく、科学や学問でも、直接的に観察できないものも多いため、このような間接的に観察する方法が活躍しています。このようにして、仮説の正しさを積み上げることで、学問の知識は構成されています。
しかし、演繹法を応用した間接的な観察方法による仮説検証には少し不安を感じた人も多いかと思います。
まず、間接的に観察するために、仮説を真と仮定して、それを前提として演繹法を用いましたが、仮説を真と仮定すること自体が許容されるのか、ということです。確かに、演繹法による推論で結論にも矛盾がないからといって、前提も正しいと言うのは少し無理があるように感じます。
ここで思い出して欲しいのですが、演繹法自体は、前提や結論の命題の内容それ自体の正しさについては何にも触れていませんでした。演繹法は、推論の形式を満たしていれば、論理的に必然的に結論も正しくなるという性質を持つだけです。それでは、日頃の論理的思考において、演繹法で使う前提が真だとしてしまっているのは何故でしょうか。
勘のいい人は分かったかと思いますが、演繹法で使う真とされる前提は、元を辿れば帰納法で多くの事実を集めて推論することで正しいらしいと分かっている命題です。つまり、演繹法で使う真とされる前提は、帰納法で導かれた命題であり、絶対に正しいと断言できるものは非常に少なく、正しいらしいという蓋然性の下で、真として扱っていることになります。
この演繹法と帰納法の関係を踏まえると、観察可能な事実を演繹法によって確定した後でも、事例が1つでは不安になるのも当然と言えます。そこで、観察事実を多く集めて仮説を検証することで、仮説推論が正しいことを確固なモノにしていくことが重要になります。そして、ここで中心となるのが、枚挙的帰納法、つまり、狭義の帰納法です。
(6.2.1)の事例が1つのみだと、たまたま海辺で魚を丸呑みした動物が、内陸部に移動して、消化する前に何かしらの要因で化石となった可能性も捨てきれません。こうした可能性を否定するにはどうすればいいでしょうか。仮説たる「この一帯の陸地は昔海であった」が正しいのならば、「海辺が近くない陸地で魚の化石が発見された」が観察されるわけですから、魚の化石が、1つだけでなく、たくさん発見できればいいことになります。そこで実際に、その一体の陸地の化石の発掘調査を大規模にしてみます。
| (6.2.3)観察可能な事実の検証 <前提1> 海辺が近くないこの一帯の陸地で、ある魚 A1の化石が発見された <前提2> 海辺が近くないこの一帯の陸地で、ある魚 A2の化石が発見された [結論 ] 海辺が近くないこの一帯の陸地で魚の化石が発見される |
こうして、魚の化石が多く見つけることができたとします。
これだけ多く魚の化石が発掘できたというコトは、「海辺が近くないこの一帯の陸地で魚の化石が発見される」という予言された観察可能な事実が多く存在するコトになります。狭義の帰納法によって、「海辺が近くないこの一帯の陸地で魚の化石が発見される」は正しい命題だ、と結論づけられます。
このように、仮説形成の後で演繹法によって予言した観察可能な事実が多く観察されたわけですから、こうしたことが観察される理由の説明である「この一帯の陸地は昔海であった」という仮説が正しい確率も、断然高まることになります。
図6.1.仮説検証と観察可能な事実
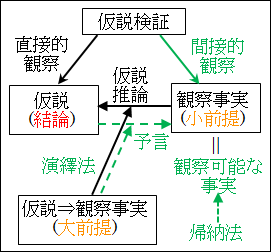
もちろん、これも帰納法による推論が用いられているので、正しい確率が高いという蓋然性でしかありません。とはいえ、仮説が間違っていると否定するほどの証拠が見つかっていない上に、仮説が正しいなら観察できるはずの事実が多く確認できているのだから、正しいとして扱っても問題はないと言えます。
さらに、魚の化石の発掘調査で、魚以外の海の生物の化石、例えば貝や海藻や蟹やエビといったものが発掘されれば、仮説「この一帯の陸地は昔海であった」が正しい確率がより高くなります。
この場合、「この一帯の陸地で魚の化石が発見される」は、「この一帯の陸地で海の生物の化石が発見される」というものに修正すべきかもしれません。いずれにしろ、「海の生物の化石」は、「魚の化石」の上位概念、つまり、「魚の化石」を含んだより広い概念なので、仮説「この一帯の陸地は昔海であった」が正しいことを強化する方向に働きます。
逆に、魚の化石が少量しか発見できず、魚以外の化石も特に見つからず、陸上の動物の化石が大量に見つかると、仮説「この一帯の陸地は昔海であった」が正しい確率は低くなり、むしろ間違っている確率が高くなります。つまり、仮説「この一帯の陸地は昔海であった」は正しい、とは言えないことになります。
なお、化石の発掘の際には、同時代に形成された同一の地層から出てくる必要があります。火山運動や地殻運動、水流の要因によって地層は長い期間をかけて形成されますが、それでも時代によって、形成される地層は異なります。したがって、同じ時代に形成された地層は、違う時代に形成された地層と異なるものになります。同時代の地層とは異なる時代の地層から化石が色々見つかっても今回の仮説には影響を特に与えません。この意味が理解できない人は、中学校の地層の知識を復習してください。
このようにして、仮説形成段階を終えて仮説検証段階に移るが、仮説の事実を直接的に観察できない場合には、演繹法によって観察可能な事実を予言して、仮説を間接的に観察します。
そのとき、1つの事例では証拠として弱いので、多くの事例を帰納法によって観察して推論していくことになります。そして、演繹法で予言された観察可能な事実を十分に多く集められた場合は、仮説推論が正しいものとして扱えるようになります。逆に、観察可能な事実が十分に集まらなかったり、それとは矛盾する事実が観察された場合には、仮説推論は誤りということになります。
| 観察可能な事実の検証←帰納法の利用 <前提1> 予言された観察可能な事実 A1 <前提2> 予言された観察可能な事実 A2 [結論] 予言された観察可能な事実は存在する → 多く観察されるほど、仮説の正しい確率は上がる |
6 まとめ
少し長くなりましたし、色々と話が行ったり来たりしたので、仮説推論についてまとめておきます。
大きくまとめると、
仮説推論による仮説形成
↓
演繹法による観察可能な事実を予言
↓
帰納法による仮説検証
の3段階に分けられました。
まず、仮説推論は、仮言三段論法の後件肯定の形式となっていました。
| 仮説推論 <大前提> P ⇒ Q <小前提> Q である (観察事実) [結論] よって、P である (仮説) 仮言三段論法の後件肯定 → 演繹法では正しくない推論 → 仮説推論では許容される推論 |
ある事実を観察することで、それを合理的に説明する仮説を形成します。
そのとき、観察事実「Q である」が小前提となり、大前提「P ⇒ Q」の後件肯定となります。
そして、結論として「P である」が導かれ、これが仮説となります。
図6.2.仮説推論の構造
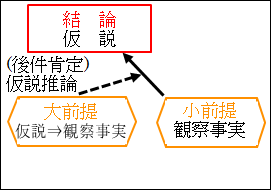
このようにして、ある観察事実から推論によって仮説を構築する仮説形成段階と言いました。
仮言三段論法の後件肯定は、演繹法で考えると正しい推論とは言えませんが、仮説推論では許容される推論となります。
また、大前提「P ⇒ Q」は、論理的思考によって導かれたモノと言うよりは、自分の中の経験や直観等によって「思いつく」ものである傾向があります。
さて、仮説推論は許容されるといっても、正しい推論であるとまでは言えませんでした。そこで、仮説推論が正しいことを確認しなければなりません。この仮説が実際に正しいことを調べることを仮説検証段階と言いました。
仮説の事実を直接的に観察できる場合は、その事実を直接的に観察して、仮説の真・偽を確かめればよいです。
図6.2.仮説推論の構造
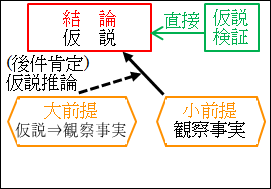
仮説の事実を直接的に観察できない場合は、仮説の事実を間接的に観察する必要があります。そこで、間接的に観察して仮説検証を行うために、観察可能な事実を予言することになります。
| 観察可能な事実の予言←演繹法の利用 <小前提> 仮説形成段階の仮説[結論] P である (真と仮定) <大前提> 仮説形成段階でも大前提 P ⇒ Q (仮説形成段階でも使用 真と仮定) [結論] 仮説形成段階の観察事実=小前提 Q である (仮説から予測される観察事実) |
最初に、形成された仮説「P である」を真と仮定します。これが小前提になります。
次に、仮説形成段階で仮説を導くために利用した大前提「P ⇒ Q」そのまま大前提として利用します。
そうすると、これは仮言三段論法の前件肯定になるので、演繹法として正しい推論となり、結論「Q である」も必然的に正しくなります。
結論「Q である」は、仮説「P である」が真ならば当然に観察されるはずのモノであることが分かります。
これが観察可能な事実の予言となります。観察可能な事実は、仮説形成段階で最初の疑問の始まりであった観察事実(小前提)であることが多いです。
図6.2.仮説推論の構造
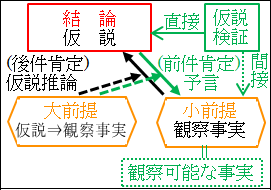
観察可能な事実の予言ができれば、後は、観察可能な事実を実際に観察できるかどうか確かめます。
| 観察可能な事実の検証←帰納法の利用 <前提1> 予言された観察可能な事実A1 <前提2> 予言された観察可能な事実A2 [結論] 予言された観察可能な事実は存在する |
予言された観察可能な事実を多く観察することで、仮説推論が正しい蓋然性を高めていきます。どれだけ予言された観察可能な事実を集めればいいかは、場合によりけりですが、多ければ多いほどいいのが基本です。
この予言された観察可能な事実を収集している過程で、観察可能な事実と矛盾・対立する事実が発見されたり、そもそも観察可能な事実が十分な数集まらないと、仮説推論は正しいとは言えないことになります。
図6.2.仮説推論の構造
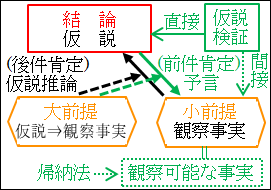
このようにして、仮説推論は行われることになります。
もちろん、たったの一回で、仮説推論から仮説検証を経て正しいと言える仮説がつくられることは少ないです。仮説形成と仮説検証を行ったり来たりして、当初の仮説を修正しながらより合理的な説明と磨き上げていくのが普通になります。
補足 説の種類
なお、今まで「仮説が正しい」とか「間違っている」とかいう表現を無批判に使ってきましたが、帰納法を用いて仮説の正しさを証明している時点で、「正しい」という言葉が必ず使えるとは限りません。そこで、厳密な論理で可能な限りありのままに事実を論じたい学問において、「仮説が正しい」という表現されることについて考えてみます。学問では、仮説が正しいとされることを、仮説は支持されると言います。
仮説が正しいといっても、明確に間違ったモノとして否定されていないという意味であり、帰納法で推論した結果として正しい確率が高いという意味であるためです。「正しい」という言葉を使わずに、正しいコトが「支持される」とすることで、一歩退いた表現をするようにしています。絶対に正しいということは難しく、常に仮説を否定する事実が発見される可能性があることからも、この「支持される」という表現がより適切だというのが分かります。
逆に、仮説が誤っている場合は、仮説は破棄されると言います。
仮説が正しいとは言えそうにないので、その仮説を採用するのができず、捨てることになるため、「破棄」という言葉を使っています。「正しい」と言うのがはばかられたように、何か見落としていたために仮説が「誤り」に見えているだけかもしれないので、明確に「誤り」と表現するよりも、捨てるという意味で「破棄」するという言葉の方が適切だとも言えます。
そして、支持された仮説は、様々な学者や第三者が独自に再度検証します。この第三者による再度の仮説検証を追試と言います。
一人では、どうしても見落としている前提や論理の飛躍が生じたり、さらには意識的にしろ無意識にしろ仮説に都合の良い事実ばかりを集めていたりしまうこともあります。そこで、追試が行われることで、仮説はより客観的に正しいことが証明されていき、その正しい確率が高まって行きます。もちろん、追試の過程で、矛盾する事実や論理破綻が見つかると、仮説が破棄されます。破棄されないまでも、より合理的な説明になるように修正されることもあります。
こうした度重なる追試の結果、学問の中で確立した仮説は定説や通説になります。
定説は、確「定」的な「説」です。
定説と言えども仮説ではあるので、将来覆される可能性はあります。しかし、多くの人が追試して確認することで、誰がやっても同じような結果が導けて、さらに仮説を覆すような事実も、少なくも今現在では、観察されないだろうと誰もが認めているような仮説です。そのため、ある事実を最も合理的に矛盾なく説明できるている説と言えます。ほぼすべての人や学者が正しいものと考えている、つまりは、支持している仮説が定説となります。
通説は、広く「通」用している「説」です。
定説程には確定的ではないが、多くの人が正しいと考えている仮説です。定説と異なる理由は、追試の結果として仮説が正しいのは間違いなさそうだが、どこかしらに見落とした前提や論理の飛躍があったり、または、ありそうだったり、完全に正しいと証明できない場合には、ほぼすべての人や学者が支持することは中々ないからです。しかし、小さな穴が仮説にあったとしても、一応は妥当で合理的な説明であると考えられるので、多くの人や学者は仮説を支持することになります。そうした人たちが多数派を形成して、仮説を支持することで、通説と呼ばれるようになります。
追試が行われている途中だったり、通説が未だ定まっていないような分野では、単に多数説と呼ばれることもあります。通説と呼ぶには支持する人数が少なかったり、仮説として穴もあるが、多数の人が支持する仮説ということで、多数説です。
通説との違いをより明らかにするためにもう少し詳しく言うと、通説は、自分の意見は別にしても、その論理や主張の正しさは支持する人や学者が多い仮説となります。
これに対して、多数説は、多くの人が支持する仮説であることは通説とは同じですが、反対の意見を持っている人が、その論理や主張の正しさまでも支持しているわけではないという点で通説とは異なります。
多数説の逆に、少数説もあります。少数説は、仮説を支持する人数が少ない場合に少数説と呼ぶことになります。多数説と少数説は、支持する人の多さで決まるわけですから分かりやすいかと思います。
通説や多数説まではいかないまでも、一定の少なくない人が支持する仮説は、有力説と呼ばれます。
有力説は、通説や多数説程には多数の人が支持しているわけではないが、通説や多数説の論理や主張に対抗するような仮説です。通説ならば絶対に正しいというわけではなく、何かしらの弱点があるから定説になっていないわけです。その弱点を指摘したり、克服したりしている仮説が有力説となります。したがって、通説のみに頼って議論を展開することは難しくなり、有力説について触れる必要が出て来ることが多いです。
多数説と有力説が組み合わさって、多数有力説という表現も偶に聞いたりします。また、少数の人しか支持していなくても少数有力説と聞いたりすることもあります。多数説なのか有力説なのかといったものは、言葉を使う人や話されている分野によって差が出て来るので、ある分野を勉強し始めたばかりの時は、あまり気にしなくてもいいかと思います。
今紹介した様々な説の関係を図表で表してみます。
承認者数の過多で説を並べてみます。承認者数とは仮説が支持されるものと認めた人の数です。承認者数が多ければ多いほど多くの人が正しいものとして扱ってもよいと考えていることになります。

承認者数が多ければ多いほど、仮説が支持されていることになるわけですから、承認者数に比例して仮説が正しい確率が上がると考えてみます。ですから、縦軸に確からしさを追加し、各説を確からしさの度合いで並べてみます。
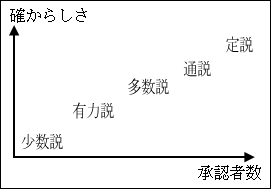
縦軸の確からしさは、仮説の確からしさの度合いです。蓋然性と言ってもいいですし、正しい確率の高さです。上に行けばいくほど確からしさは高まります。
多数有力説等、呼称が組み合わされることもありました。また、仮説は新しい事実等によって修正されることもありました。しがたって、点というより幅を持ったものと考えられます。
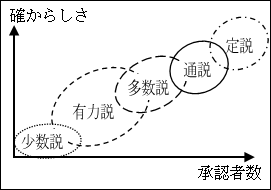
説の承認者数や確からしさが重なりあうこともあるのが、はっきりと見てとれます。
ですから、時の流れと共に、かつて有力説だったものが多数説になり、さらには通説になり、そして定説になる可能性があることも理解できます。
もちろん、この図は各説の関係の理解を助けるために描いたものですから、すべての分野ですべての説がこのように分類できるというわけではありません。あくまで、典型的な各説の関係を表したものと思っておいてください。
前頁:第5章 帰納法
ページトップへ:第6章 仮説推論
次頁:第7章 類比推論